WmmmmJ-算法第二章上机实践报告（配有图解）

实践报告任选一题进行分析。内容包括：

  1. 实践题目
  2. 问题描述
  3. 算法描述
  4. 算法时间及空间复杂度分析（要有分析过程）
  5. 心得体会（对本次实践收获及疑惑进行总结）

1.实践报告：

　　已知有两个等长的非降序序列S1, S2, 设计函数求S1与S2并集的中位数。有序序列A​0​​,A​1​​,⋯,A​N−1​​的中位数指A​(N−1)/2​​的值,即第⌊(N+1)/2⌋个数（A​0​​为第1个数）。

　　输入格式:

　　　　输入分三行。第一行给出序列的公共长度N（0<N≤100000），随后每行输入一个序列的信息，即N个非降序排列的整数。数字用空格间隔。

　　输出格式:

　　　　在一行中输出两个输入序列的并集序列的中位数。

2.问题描述：

　　需要求两个等长的非降序序列的并集的中位数。时间复杂度要求在O（logN）

3.算法描述：

　　1）基本方法：看到非降序并且时间复杂度也提示了需要使用二分查找法中位数。在此题我用了递归求解。

　　2）递归条件：当切割的子数列只剩一个元素的时候，返回较小的那个数。

return a[La] > b[Lb] ? b[Lb]:a[La];

 

　　3）解题过程：

　　　　①每次递归都对两条数列求解各自的中位数并进行比较，若当前的Mid_A比Mid_B要大，下一次递归就取A左边的子数列（即较小的子数列）和B右边的子数列；反之亦然。

　　　　②在进行下一次递归之前若此时两条的公共N是偶数（即此时两条数列都是偶数数列）那么在进入到下一次递归之前，较大数列的中位数要先加一。

例如：

　　　　1st：

　　　　

　　　　2nd：

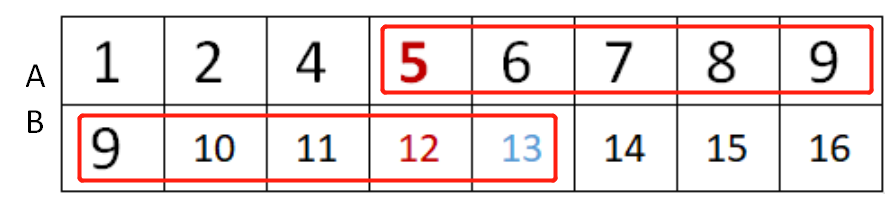　　　　因为这是偶数数列所以Mid_B++；

　　　　3rd：

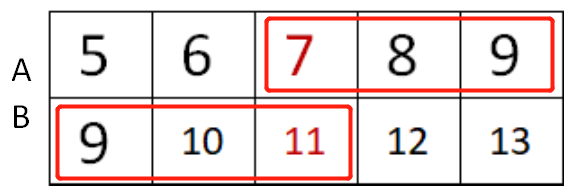　　　　这是奇数数列不做任何操作。

　　　　4th：

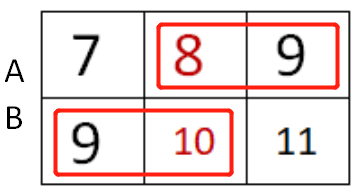　　　　此时又是奇数数列不作任何操作；

　　　　5th：

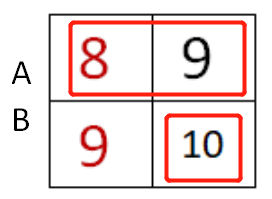　　　　此时是偶数数列，所以Mid_B++；

 

 

　　　　6th：

　　　　最后只剩下最后两个数字了，即满足返回递归的条件

 　　4）难点&疑点：

　　　　①为什么要数列的中位数较大的那一个需要先加一？

　　　　因为：在偶数数列中用此方法（n-1）/ 2求解两次中位数会使得所求的数字左移一位，所以为了使得每次比较的Mid_A与Mid_B都刚好处于并集的正中间（准确说是要大于左边的两个数列加在一起的N-1个数字）

　　　　即：左边蓝色的数字个数刚好是5+2 = n-1（即8-1=7个）

　　　　

 

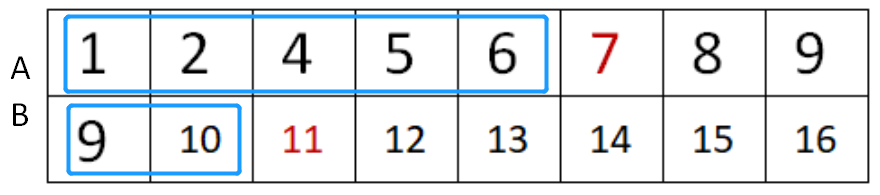
　　　　　　　　　　　　　　  图一

 

 　　　　②那为什么第一次递归进来的数列两个Mid只比六个数字要大呢？

             

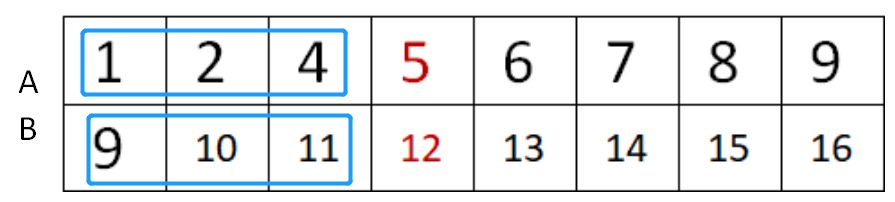
　　　　　　　　　　　　　　 图二

　　　　因为：第一次进来如果刚好是偶数数列，我们不必担心此时会返回错误的答案，还记得我们的返回条件是当数组只剩下一个数字吗？而且我们跳进下一次循环之后就都是比N-1个数字要大了（如图二）。

　　5）代码展示：

 1 #include<iostream>
 2 using namespace std;
 3 int a[100001], b[100001];
 4 int find_mid(int La, int Lb, int Ra, int Rb){
 5     if(La == Ra && Lb == Rb) return a[La] > b[Lb] ? b[Lb]:a[La];
 6     int m1 = (La + Ra) / 2;
 7     int m2 = (Lb + Rb) / 2;
 8     if (a[m1] < b[m2]) {
 9         Rb = m2;
10         if((Ra - La) % 2) {
11             m1++;
12         }
13         La = m1;
14     }
15     else {
16         Ra = m1;
17         if ((Rb - Lb) % 2) {
18             m2++;
19         }
20         Lb = m2;
21     }
22     return find_mid(La, Lb, Ra, Rb);
23 }
24 int main() {
25     int n;
26     cin >> n;
27     for (int i = 0; i < n; ++i){
28         cin >> a[i];
29     }
30     for (int i = 0; i < n; ++i){
31         cin >> b[i];
32     }
33     cout << find_mid(0, 0, n - 1, n - 1);
34 }
分治递归

 

4.算法时间及空间复杂度分析：

　　1）时间复杂度O（logN）：运用了二分法查找，每次递归进去都使得问题规模减半。

　　2）空间复杂度O（1）：没有使用辅助数组。

 5.心得体会：

　　1）仔细审题：一开始没用使用分治的思想去解这道题，反而是用来merge的思想去用归并的方法，结果发现忘记考虑时间复杂度了。后来用来二分法一直在考虑临界条件，其实并不用这么复杂，只要另最后跳出的条件是只要求两个数组都只剩最后一个数字就好了。

　　2）虚心请教：这道题有一个难点就是会容易忽略偶数数列的中位数求解左移问题。我自己死磕了半天，结果在请教了罗同学之后恍然大悟。这么小的问题不应该耽误这么久的时间，所以以后不要再反复的浪费时间测试，不如换个思路，多多请教同学与老师。

posted @ 2019-09-22 10:56  Winston-wmj  阅读(312)  评论(0)  编辑  收藏  举报