『嗨威说』算法设计与分析 - STL中Sort函数的实现原理初探
本文索引目录：
一、对Sort算法实现的个人阅读体会
二、Sort算法使用的三个排序算法的优点介绍
2.1 插入排序的优缺点
2.2 堆排序的优缺点
2.3 快速排序的优缺点
2.4 新的结合排序——内省式排序的出现
三、sort函数的具体实现
四、尾录
一、对Sort算法实现的个人阅读体会：
如同《STL源码剖析》中所说，人类生活在一个有序的世界中，没有排序，很多事情无法进展，但是对于排序来说，面对大数据的排序存在着效率的问题。我们不可能说对十万个数进行冒泡排序，这在时间成本上是极不现实的。所以，STL为了追求效率极致，结合三大较为快速的排序：快排、堆排、插排来实现对大数据的排序。
STL是C++非常出色和有较高效率的代码框架，以优化得到更高效率为目标的大作品，更加的体现了C++的高效率。在STL中，有一个排序函数sort无不把这一目标体现得淋淋尽致。为了得到更快的排序效率，sort函数根据序列的大小，自动地合理使用快排（Quick Sort）、插排（Insertion Sort）和堆排（Heap Sort）。
STL的开发者还非常有意思，通过多个方面来决定这三个排序的使用，例如当问题规模较少时，为了减少递归函数调用的资源占用，则采取插排来迅速对小额数据量完成排序，在数据量不大时，插排的速度效率完全是可以超过快排的。当问题规模适中时，STL可以先进行快排，然后当快排递归分组的序列组达到一定小的问题规模时，同上实行插排，完成小额排序的任务。当问题规模过大时，STL开发者考虑到了快排调用递归层的深度，为了防止递归层过深过多，面对大额数据量时，会改用堆排。
这或许就是算法工程师的魅力吧，追求高效的算法，也映射出了一些道理，在今后的工作学习生活中，一个高效的工作/生活/学习算法，能给你带来多大的效益，因此摸索更高效的方法尤为重要。
二、Sort算法使用的三个排序算法的优点介绍：
2.1 插入排序的优缺点：
插入排序不适合对于数据量比较大的排序应用。但是，如果需要排序的数据量很小，例如，量级小于千；或者若已知输入元素大致上按照顺序排列，那么插入排序还是一个不错的选择。插入排序最好时间复杂度为O(n)、最坏时间复杂度为O(n^2)，空间复杂度为O(1)，属于稳定排序。
2.2 堆排序的优缺点：
堆排序经常是作为快速排序最有力的竞争者出现，它们的复杂度都是O(N logN)。但是，有一点它却比快速排序要好很多：最坏情况它的复杂度仍然会保持O(N logN)，这一优点对本文介绍的新算法有着巨大的作用。
2.3 快速排序的优缺点：
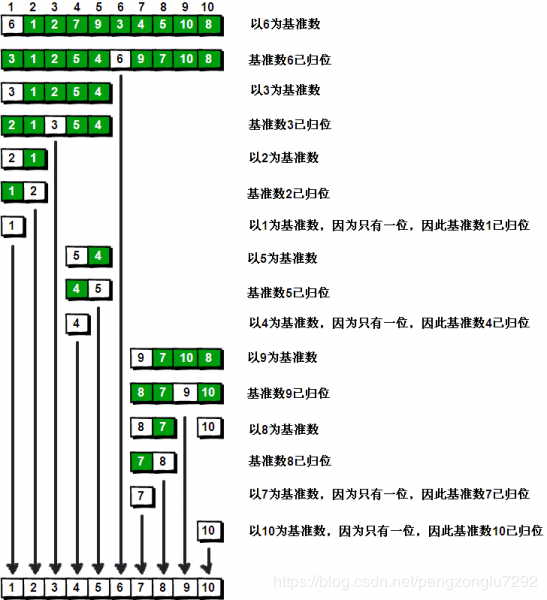
快速排序的优点无疑就是在内排序最快的排序了，时间复杂度可以达到O（NlogN），但是可能由于不当的pivot选择，导致其在最坏情况下复杂度恶化为O(N2)。另外，由于快速排序一般是用递归实现，我们知道递归是一种函数调用，它会有一些额外的开销，比如返回指针、参数压栈、出栈等，在分段很小的情况下，过度的递归会带来过大的额外负荷，从而拉缓排序的速度。
2.4 新的结合排序——内省式排序的出现：
由于快速排序有着前面所描述的问题，因此Musser在1996年发表了一遍论文，提出了Introspective Sorting(内省式排序)。它是一种混合式的排序算法，集成了前面提到的三种算法各自的优点：
=》在数据量很大时采用正常的快速排序，此时效率为O(logN)。
=》一旦分段后的数据量小于某个阈值，就改用插入排序，因为此时这个分段是基本有序的，这时效率可达O(N)。
=》在递归过程中，如果递归层次过深，分割行为有恶化倾向时，它能够自动侦测出来，使用堆排序来处理，在此情况下，使其效率维持在堆排序的O(N logN)，但这又比一开始使用堆排序好。
由此可知，它乃综合各家之长的算法。也正因为如此，C++的标准库就用其作为std::sort的标准实现。
三、sort函数的具体实现：
注意：若要使用sort函数，需要包括头文件#include<algorithm>。
在老师推荐的《STL源码剖析》给出了sort的函数原型：
template <class RandomAccessIterator> inline void sort(RandomAccessIterator first, RandomAccessIterator last) { if (first != last) { __introsort_loop(first, last, value_type(first), __lg(last - first) * 2); __final_insertion_sort(first, last); } }
我们可以发现，sort函数需要针对RandomAccessIterator，这是一个随机存取迭代器，一般针对数组、结构体数组、类数组、vector容器、deque使用，其他的容器一般有内置的sort排序算法。
首先if判断序列区间的有效性，不是单个对象，接着调用__introsort_loop，在该函数结束之后，最后调用插入排序（__final_insertion_sort）。
对于__introsort_loop函数STL展示如下：
template <class RandomAccessIterator, class T, class Size> void __introsort_loop(RandomAccessIterator first,RandomAccessIterator last, T*,Size depth_limit) { while (last - first > __stl_threshold) { if (depth_limit == 0) { partial_sort(first, last, last); return; } --depth_limit; RandomAccessIterator cut = __unguarded_partition(first, last, T(__median(*first, *(first + (last - first)/2),*(last - 1)))); __introsort_loop(cut, last, value_type(first), depth_limit); last = cut; } }
在这函数中：可以看出它是一个递归函数，因为我们说过，Introspective Sort在数据量很大的时候采用的是正常的快速排序，因此除了处理恶化情况以外，它的结构应该和快速排序一致。除此之外，STL还使用了三点中值法来防止排序恶化。
除了以上两个特点
·递归函数
·三点中值为标记
STL还针对partition分割函数进行了优化，并在书中给出了非常简单明了的图解：
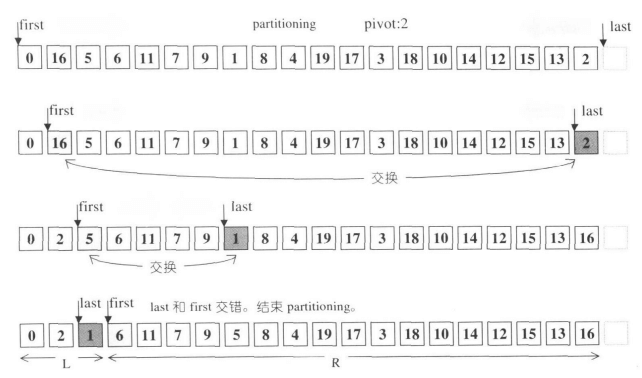
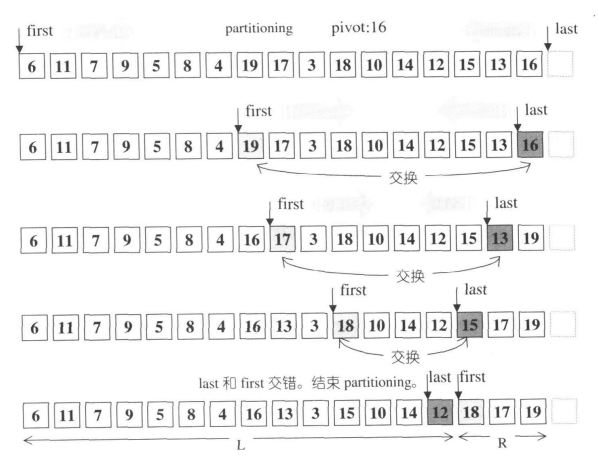
最后STL还对递归深度进行了实时判断：
·递归深度
__introsort_loop函数中的depth_limit是前面所提到的判断分割行为是否有恶化倾向的阈值，即允许递归的深度，调用者传递的值为2logN。注意看if语句，当递归次数超过阈值时，函数调用partial_sort，它便是堆排序，堆排序结束之后直接结束当前递归。
·最小分段阈值
除了递归深度阈值以外，Introspective Sort还用到另外一个阈值。注意看__introsort_loop中的while语句，其中有一个变量__stl_threshold，其定义为：const int __stl_threshold = 16;
它就是我们前面所说的最小分段阈值。当数据长度小于该阈值时，再使用递归来排序显然不划算，递归的开销相对来说太大。而此时整个区间内部有多个元素个数少于16的子序列，每个子序列都有相当程度的排序，但又尚未完全排序，过多的递归调用是不可取的。而这种情况刚好插入排序最拿手，它的效率能够达到O(N)。因此这里中止快速排序，sort会接着调用外部的__final_insertion_sort，即插入排序来处理未排序完全的子序列。
对于__final_insertion_sort函数原型展示如下：
template <class RandomAccessIterator, class T> void __unguarded_linear_insert(RandomAccessIterator last, T value) { RandomAccessIterator next = last; --next; while (value < *next) { *last = *next; last = next; --next; } *last = value; } template <class RandomAccessIterator, class T> inline void __linear_insert(RandomAccessIterator first, RandomAccessIterator last, T*) { T value = *last; if (value < *first) { copy_backward(first, last, last + 1); *first = value; } else __unguarded_linear_insert(last, value); } template <class RandomAccessIterator> void __insertion_sort(RandomAccessIterator first, RandomAccessIterator last) { if (first == last) return; for (RandomAccessIterator i = first + 1; i != last; ++i) __linear_insert(first, i, value_type(first)); }
STL的插入排序和我们之前在数据结构课程中所学的插入排序还略有不同，在STL的插入排序中用到了一些很妙的优化效率解决方式，但鉴于我的表达能力有限，为了不误导他人对sort里插排的理解，就不在此赘述讲解。
四、尾录：
非常感谢侯捷的《STL源码剖析》以及老师推荐的feihu作者，在脑海中或者笔记上总结，和汇聚成文相比完全是两回事，有太多的背景要介绍，述说的方式，结构的安排等等无一不需花费心思。现在可以体会出每个写作者的艰辛之处，更对认真完成众多经典作品的作者们充满了敬佩。确实如此，就连我在简单编写浅显的博客的时候，都得思考如何排版结构阐述、合理解释，这都需要花费不少心思和精力，但这些优秀作品无疑能给他人带来巨大帮助，为此以这些优秀的作者为目标，希望能够有机会分享富有高质量高水平的知识点讲解给有需要的人。
如有不合理的地方，请及时指正，我愿听取改正~
