『嗨威说』数据结构 - 第六章学习内容小结
本文主要内容:(与树类似)
一、图的概念
二、图的重中之重——两种重要存储结构
三、树的升级拓展应用:最小生成树
四、本节应用习题
五、个人反思与未来计划
一、图的基本概念:
(1)图的定义:
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
注意:线性表中可以没有元素,称为空表。树中可以没有结点,叫做空树。但是在图中不允许没有顶点,可以没有边。
(2)图的基本术语:
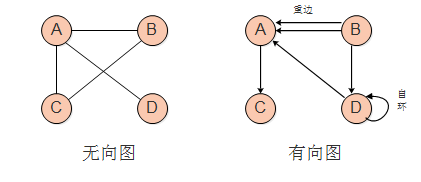
· 无向边:若顶点Vi和Vj之间的边没有方向,称这条边为无向边,用 (Vi,Vj)来表示。
· 无向图:图中任意两个顶点的边都是无向边。
· 有向边:若从顶点Vi到Vj的边有方向,称这条边为有向边,也称为弧,用 <Vi, Vj> 来表示,其中 Vi 称为弧尾,Vj 称为弧头。
· 有向图:图中任意两个顶点的边都是有向边。
· 简单图:不存在自环(顶点到其自身的边)和重边(完全相同的边)的图。
· 稀疏图;有很少条边或弧的图称为稀疏图,反之称为稠密图。
· 权:表示从图中一个顶点到另一个顶点的距离或耗费。
· 网:带有权重的图。
· 度:与特定顶点相连接的边数。
· 出度、入度:有向图中的概念,出度表示以此顶点为起点的边的数目,入度表示以此顶点为终点的边的数目。
· 连通图:任意两个顶点都相互连通的图。
· 极大连通子图:包含竟可能多的顶点(必须是连通的),即找不到另外一个顶点,使得此顶点能够连接到此极大连通子图的任意一个顶点。
· 连通分量:极大连通子图的数量。
· 强连通图:此为有向图的概念,表示任意两个顶点a,b,使得a能够连接到b,b也能连接到a 的图。
· 连通图的生成树:一个极小连通子图,它含有原图中全部定点,但只有足以构成一棵树的 n-1 条变,这样的连通子图称为连通图的生成树。
· 最小生成树:此生成树的边的权重之和是所有生成树中最小的。
(3)图的两种遍历方式:
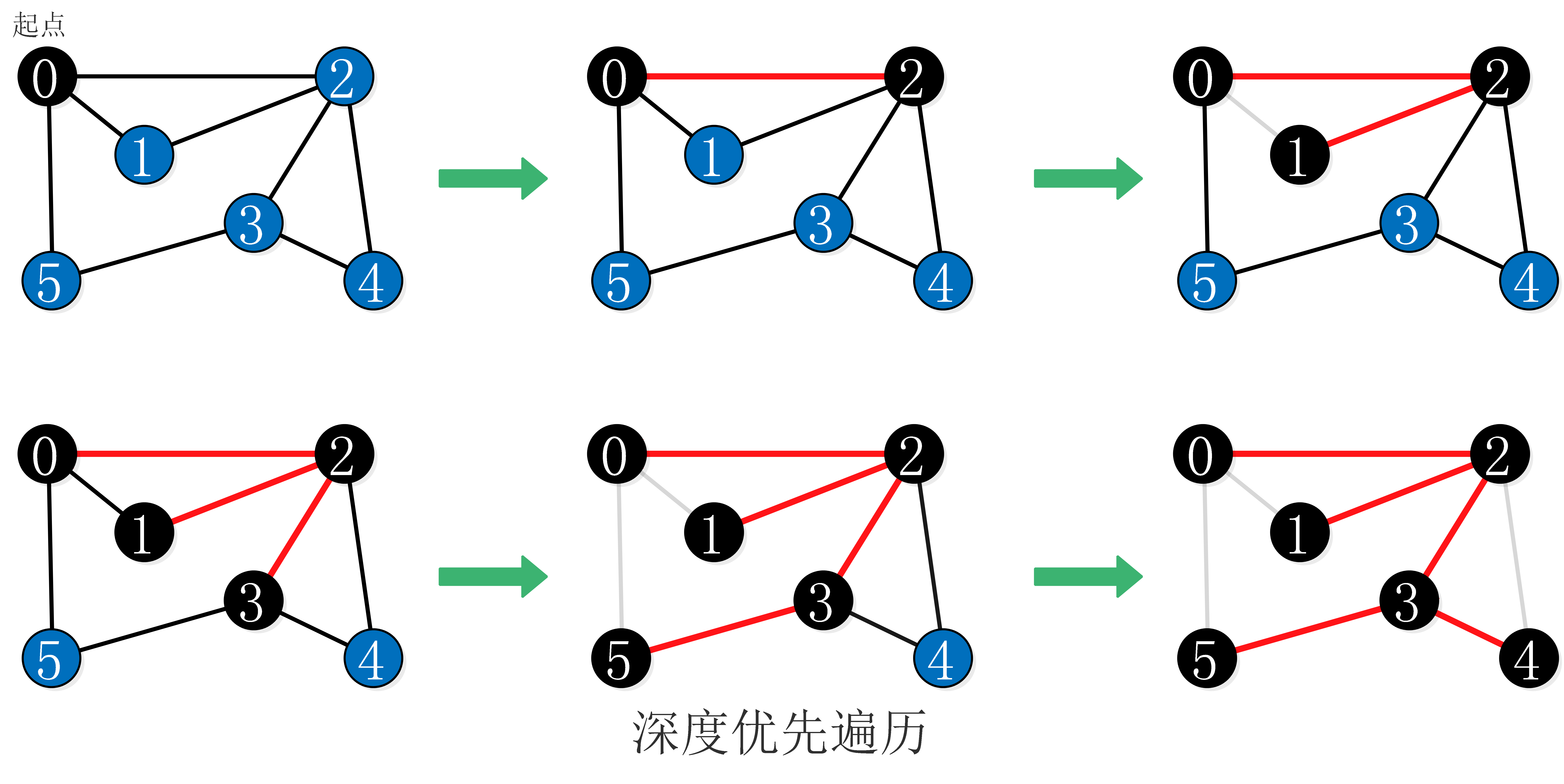
· 深度优先遍历:(DFS常利用递归思想)
首先从图中某个顶点v0出发,访问此顶点,然后依次从v相邻的顶点出发深度优先遍历,直至图中所有与v路径相通的顶点都被访问了;若此时尚有顶点未被访问,则从中选一个顶点作为起始点,重复上述过程,直到所有的顶点都被访问。
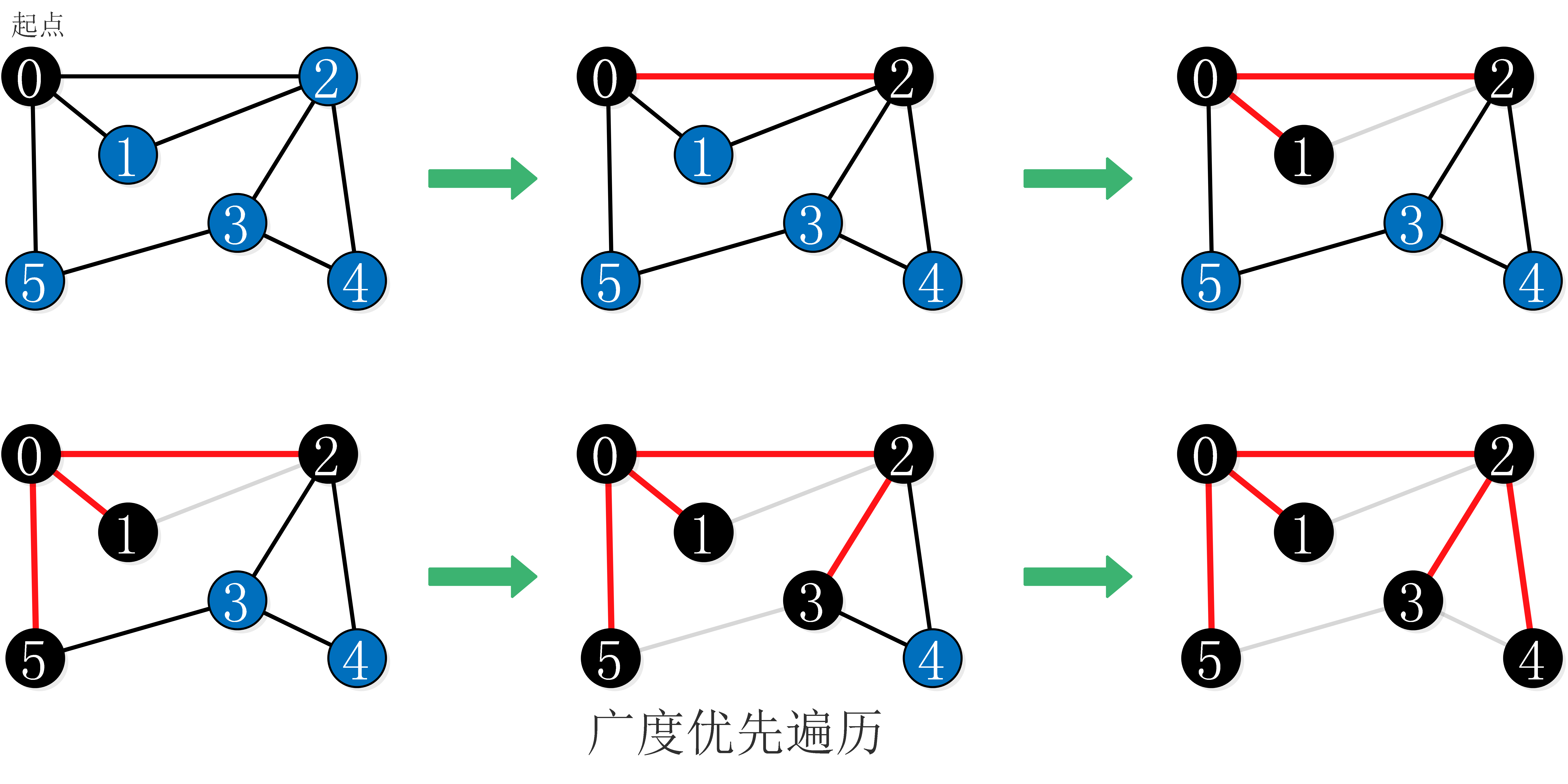
· 广度优先遍历:(BFS常利用队列+队列不为空循环思想)
首先,从图的某个顶点v0出发,访问了v0之后,依次访问与v0相邻的未被访问的顶点,然后分别从这些顶点出发,广度优先遍历,直至所有的顶点都被访问完。
二、图的重中之重 —— 已学习的两种存储结构:
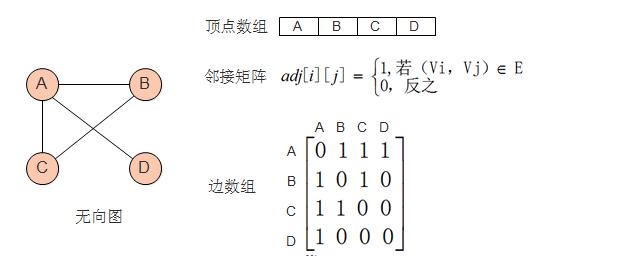
(1)邻接矩阵:
图的邻接矩阵的存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称邻接矩阵)存储图中的边或弧的信息。
优缺点:
· 优点:结构简单,操作方便
· 缺点:对于稀疏图,这种实现方式将浪费大量的空间。
(2)邻接表:
邻接表是一种将数组与链表相结合的存储方法。其具体实现为:将图中顶点用一个一维数组存储,每个顶点Vi的所有邻接点用一个单链表来存储。这种方式和树结构中孩子表示法一样。
对于有向图其邻接表结构如下:
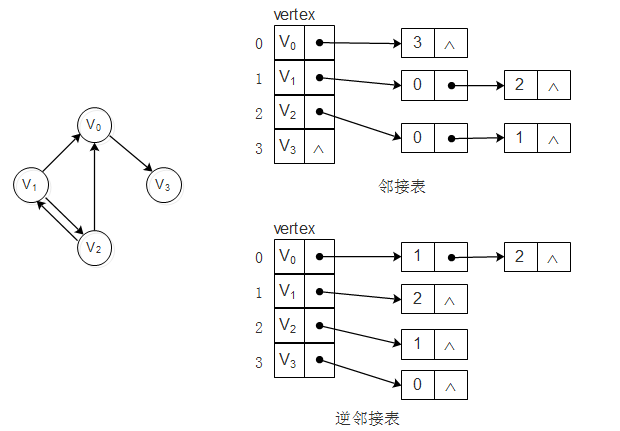
优缺点:
· 优点:本算法的时间复杂度为 O(N + E),其中N、E分别为顶点数和边数,邻接表实现比较适合表示稀疏图。
· 缺点:操作繁琐
注:还有一种十字链表存储结构,暂未教学,等学习熟练之后再单独拿来写博
三、图的升级拓展之一:最小生成树 (贪心算法):
(1)最小生成树的概念:
图的生成树是它的一棵含有所有顶点的无环连通子图。一棵加权图的最小生成树(MST)是它的一棵权值(所有边的权值之和)最小的生成树。
(2)最小生成树的两种实现算法:
· 普里姆算法(Prim)
实现过程:
从顶点0开始,首先将顶点0加入到树中(标记),顶点0和其它点的横切边(这里即为顶点0的邻接边)加入优先队列,将权值最小的横切边出队,加入生成树中。此时相当于也向树中添加了一个顶点2,接着将集合(顶点1,2组成)和另一个集合(除1,2的顶点组成)间的横切边加入到优先队列中,如此这般,直到队列为空。
· 克鲁斯卡尔算法(Kruskal)
实现过程:
按照边的权重顺序来生成最小生成树,首先将图中所有边加入优先队列,将权重最小的边出队加入最小生成树,保证加入的边不与已经加入的边形成环,直到树中有V-1到边为止。
注:具体实现代码暂未学习,仅了解实现过程,后续增加。
四、本章习题练习:
拯救007:(DFS)

在老电影“007之生死关头”(Live and Let Die)中有一个情节,007被毒贩抓到一个鳄鱼池中心的小岛上,他用了一种极为大胆的方法逃脱 —— 直接踩着池子里一系列鳄鱼的大脑袋跳上岸去!(据说当年替身演员被最后一条鳄鱼咬住了脚,幸好穿的是特别加厚的靴子才逃过一劫。) 设鳄鱼池是长宽为100米的方形,中心坐标为 (0, 0),且东北角坐标为 (50, 50)。池心岛是以 (0, 0) 为圆心、直径15米的圆。给定池中分布的鳄鱼的坐标、以及007一次能跳跃的最大距离,你需要告诉他是否有可能逃出生天。 输入格式: 首先第一行给出两个正整数:鳄鱼数量 N(≤100)和007一次能跳跃的最大距离 D。随后 N 行,每行给出一条鳄鱼的 (x,y) 坐标。注意:不会有两条鳄鱼待在同一个点上。 输出格式: 如果007有可能逃脱,就在一行中输出"Yes",否则输出"No"。 输入样例 1: 14 20 25 -15 -25 28 8 49 29 15 -35 -2 5 28 27 -29 -8 -28 -20 -35 -25 -20 -13 29 -30 15 -35 40 12 12 输出样例 1: Yes 输入样例 2: 4 13 -12 12 12 12 -12 -12 12 -12 输出样例 2: No
题目有一点点小坑,刚开始还过了五个测试点,只差一个测试点,但还好一两小时肝一下debug出来了,下面简单说一下题意:
有一个人在一个圆内,半径为7.5(这是个坑,不是15噢)单位,然后可以从圆内往外跳,但只有固定的几个点可以跳,而且能不能跳过去看这个人的最大跳跃距离。只要能跳出100*100的大矩形则说明可以逃生输出Yes,否则No
题目大意就是这样啦,简单拟定一下思路:
1、对于每一个点,用一个struct去实现其存储结构,存储其x、y坐标、能够跳到的点的编号、能够跳到点的数目、能否成为起跳点、能否成为终止点。
2、输入完x、y坐标点之后,扫一遍全点,链接能跳的点,并且判断能否成为起跳点,能否成为终止点。
3、特判一下当最大可跳距离大于42.5时,可以不用跳到鳄鱼,可以直接跳出矩形。
4、实现DFS深搜递归,打上vis数组。
现在我们来动手试一下吧~
首先,头文件,因为是ACMer选手,习惯了C语言的写法,各位小伙伴不必在意噢,只需要把scanf输入的东西换成cin,printf输出的东西换成cout就搞定了
#include<stdio.h> #include<math.h> #include<string.h> #define MAX 999
第二步,开始建立图结点的结构体:按上面我思路说的,存储其x、y坐标、能够跳到的点的编号、能够跳到点的数目、能否成为起跳点、能否成为终止点。
typedef struct ArcNode{ int x; int y; int num; int Next[MAX]; bool out = false; bool in = false; }ArcNode;
第三步,基本变量申明以及函数原型申明:
int N,maxJump,ans,vis[MAX]; void DFS(ArcNode *p,int i); void buildGraph(ArcNode *&p); void buildArc(ArcNode *&p); void searchInOut(ArcNode *&p);
第四步,对Main主函数进行模块化函数构建:
int main() { ArcNode *G; //建立结点 buildGraph(G); //导入结点内容 if(maxJump >= 42.5) //特判 { printf("Yes\n"); return 0; } buildArc(G); //扫一遍所有点,构造边,使能互相跳的点结合起来 searchInOut(G); //扫一遍所有点,判断是否能够成为起跳点和终止点 ans = -1; //答案初始化 for(int i = 1;i<=N;i++) if(G[i].in) //如果这个点是起跳点 { memset(vis,0,sizeof(vis)); //重置vis数组 DFS(G,i); //开始深搜 } if(ans == -1) printf("No\n"); //打印答案 else printf("Yes\n"); return 0; }
第五步,导入结点,比较简单:一个输入导入就可以了。
void buildGraph(ArcNode *&p) { scanf("%d %d",&N,&maxJump); p = new ArcNode[N+1]; for(int i = 1;i<=N;i++) scanf("%d %d",&p[i].x,&p[i].y); }
第六步,链接各点,实现保存可以互跳的点,这里需要两层for循环的遍历,可能效率优点不高,但简单粗暴
void buildArc(ArcNode *&p) { for(int i = 1;i<=N;i++) { for(int u = 1;u<=N;u++) { if(u == i) continue; if((maxJump * maxJump) >= (p[i].x-p[u].x)*(p[i].x-p[u].x)+(p[i].y-p[u].y)*(p[i].y-p[u].y)) //这里除了用sqrt还可以直接用平方比较,误差会小一点 { p[i].num++; p[i].Next[p[i].num] = u; //将可互跳的边导入 } } } }
第七步,搜索起始点和终止点,也是比较简单的,一个距离公式就好了。
void searchInOut(ArcNode *&p) { for(int i = 1;i<=N;i++) { if((maxJump + 7.5)*(maxJump + 7.5) >= p[i].x*p[i].x+p[i].y*p[i].y) p[i].in = true; if(maxJump >= 50 - abs(p[i].x) || maxJump >= 50 - abs(p[i].y)) p[i].out = true; } }
第八步,嵌套一下DFS递归就好了,注意递归的终止条件。
void DFS(ArcNode *p,int i) { vis[i] = 1; if(p[i].out == true) //如果搜到了这个点是终止点,说明这个人可以跳出去,那么就给答案变量做个标记。 ans = 1; if(p[i].num == 0) //递归终止条件 return; for(int u = 1; u<=p[i].num; u++) if(!vis[p[i].Next[u]])//防止递归循环需要一个标记数组 DFS(p,p[i].Next[u]); }
这样整个程序就完成啦~ 完整代码贴上:

1 #include<stdio.h> 2 #include<math.h> 3 #include<string.h> 4 #define MAX 999 5 6 typedef struct ArcNode{ 7 int x; 8 int y; 9 int num; 10 int Next[MAX]; 11 bool out = false; 12 bool in = false; 13 }ArcNode; 14 15 int N,maxJump,ans,vis[MAX]; 16 void DFS(ArcNode *p,int i); 17 void buildGraph(ArcNode *&p); 18 void buildArc(ArcNode *&p); 19 void searchInOut(ArcNode *&p); 20 int main() 21 { 22 ArcNode *G; 23 buildGraph(G); 24 if(maxJump >= 42.5) 25 { 26 printf("Yes\n"); 27 return 0; 28 } 29 buildArc(G); 30 searchInOut(G); 31 ans = -1; 32 for(int i = 1;i<=N;i++) 33 if(G[i].in) 34 { 35 memset(vis,0,sizeof(vis)); 36 DFS(G,i); 37 } 38 if(ans == -1) printf("No\n"); 39 else printf("Yes\n"); 40 return 0; 41 } 42 void buildGraph(ArcNode *&p) 43 { 44 scanf("%d %d",&N,&maxJump); 45 p = new ArcNode[N+1]; 46 for(int i = 1;i<=N;i++) 47 scanf("%d %d",&p[i].x,&p[i].y); 48 } 49 void buildArc(ArcNode *&p) 50 { 51 for(int i = 1;i<=N;i++) 52 { 53 for(int u = 1;u<=N;u++) 54 { 55 if(u == i) continue; 56 if((maxJump * maxJump) >= (p[i].x-p[u].x)*(p[i].x-p[u].x)+(p[i].y-p[u].y)*(p[i].y-p[u].y)) 57 { 58 p[i].num++; 59 p[i].Next[p[i].num] = u; 60 } 61 } 62 } 63 } 64 void searchInOut(ArcNode *&p) 65 { 66 for(int i = 1;i<=N;i++) 67 { 68 if((maxJump + 7.5)*(maxJump + 7.5) >= p[i].x*p[i].x+p[i].y*p[i].y) 69 p[i].in = true; 70 if(maxJump >= 50 - abs(p[i].x) || maxJump >= 50 - abs(p[i].y)) 71 p[i].out = true; 72 } 73 } 74 void DFS(ArcNode *p,int i) 75 { 76 vis[i] = 1; 77 if(p[i].out == true) 78 ans = 1; 79 if(p[i].num == 0) 80 return; 81 for(int u = 1; u<=p[i].num; u++) 82 if(!vis[p[i].Next[u]]) 83 DFS(p,p[i].Next[u]); 84 }
下面将具体的导入结点和DFS搜索过程打印出来,大家可以看看他的步骤流程:
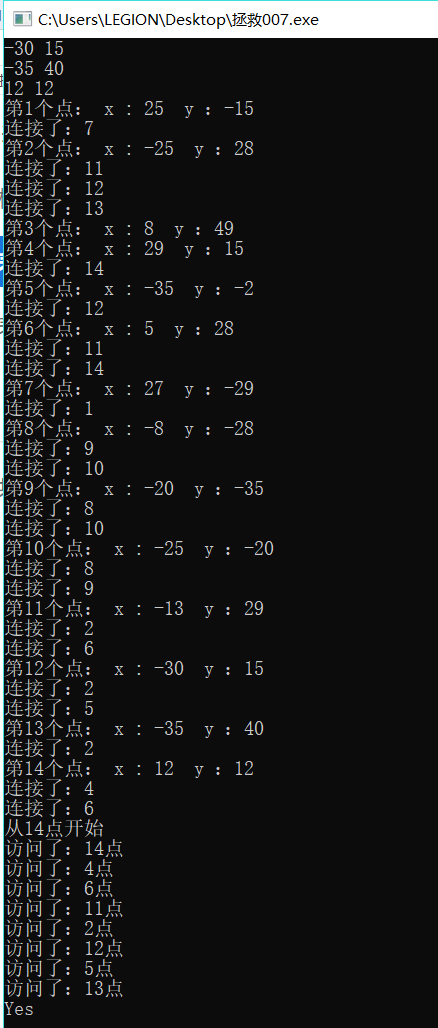
五、个人反思及未来计划:
有一天老师跟我说了一句话,让我一直留着比较深的印象:

是啊,从开学到现在一直有不少人告诉我,大家能够专心干一件事,你真的就是很棒的人了。
而我,在上学期加了五个社团,Quanta、Eddy、数挖、ACM、招协,拖着班长,拖着五个兼职,我也不知道我怎么活下来的,大概是想把自己忙成狗 吧,把一些伤心的事情忘得一干二净。
下学期收了收心,退了几个社团,仅留ACM和数挖,班长的事情随着英剧的结束事情也少了不少,兼职也拖剩了一个,慢慢收心,大概上学期各个方面的接触,也让我逐步摸清了未来的发展方向。
就这样吧,努力计划做好每天该干的事情,不负身边人对我的期望,好好对待每一个人,去努力的带给他们快乐,带给自己快乐,带来更多的动力。
大二,大概有了方向了,嗯,努力干下去。
(1)图比较抽象的数据结构上基础有些不牢,进一步学习普里姆算法、克鲁斯卡尔算法、迪杰斯特拉算法等,特别是碰到链式存储的指针使用的时候,需要找时间给自己多加强这方面的学习。
(2)ACM集训队每天几道题,每周写一篇博客。
(3)完成论文标解并准备好论文演讲『Improving patch-based scene text script identification with ensembles of conjoined networks』
(4)完成论文标解并准备好论文演讲『汉老双语命名实体识别及对齐方法研究_韩锐』






