『嗨威说』数据结构 - 第五章学习内容小结

本文主要内容：

　　一、树的概念

　　二、树的重中之重——二叉树

　　三、树的升级应用：哈夫曼树

　　四、本节应用习题

　　五、个人反思与未来计划

一、树的基本概念：

　　　　（1）树的定义：

　　　　　　　　树（Tree）：n(n >= 0)个节点构成的有限集合。

- - - 当n = 0时，称为空树；
    - 对任意一棵空树(n > 0)，它具备以下性质：
    - 树中有一个称为**根(Root)**的特殊节点，用r(root)表示；
    - 其余节点可分为m(m > 0)个互不相交的有限集T1,T2,...Tm，其中每个集合本省又是一棵树，称为原来树的子树（SubTree）

　　　　　　　　注意：　　　①子树不能相交

　　　　　　　　　　　　　　②除了根节点外，每个节点有且仅有一个父节点

　　　　　　　　　　　　　　③一个N个节点的树有N-1条边

　　　　（2）树的基本术语：

- - - 节点的度（Degree）：节点的子树个数。
    - 树的度：树的所有节点中最大的度数（树的度通常为节点个数的N-1）。
    - 叶节点（Leaf）：度为0的节点（也称叶子节点）。
    - 父节点（Parent）：有子树的节点是其子树的父节点。
    - 子节点（Child）：若A节点是B节点的父节点，则称B节点是A节点的子节点。
    - 兄弟节点（Sibling）：具有同一个父节点的各节点彼此是兄弟节点。
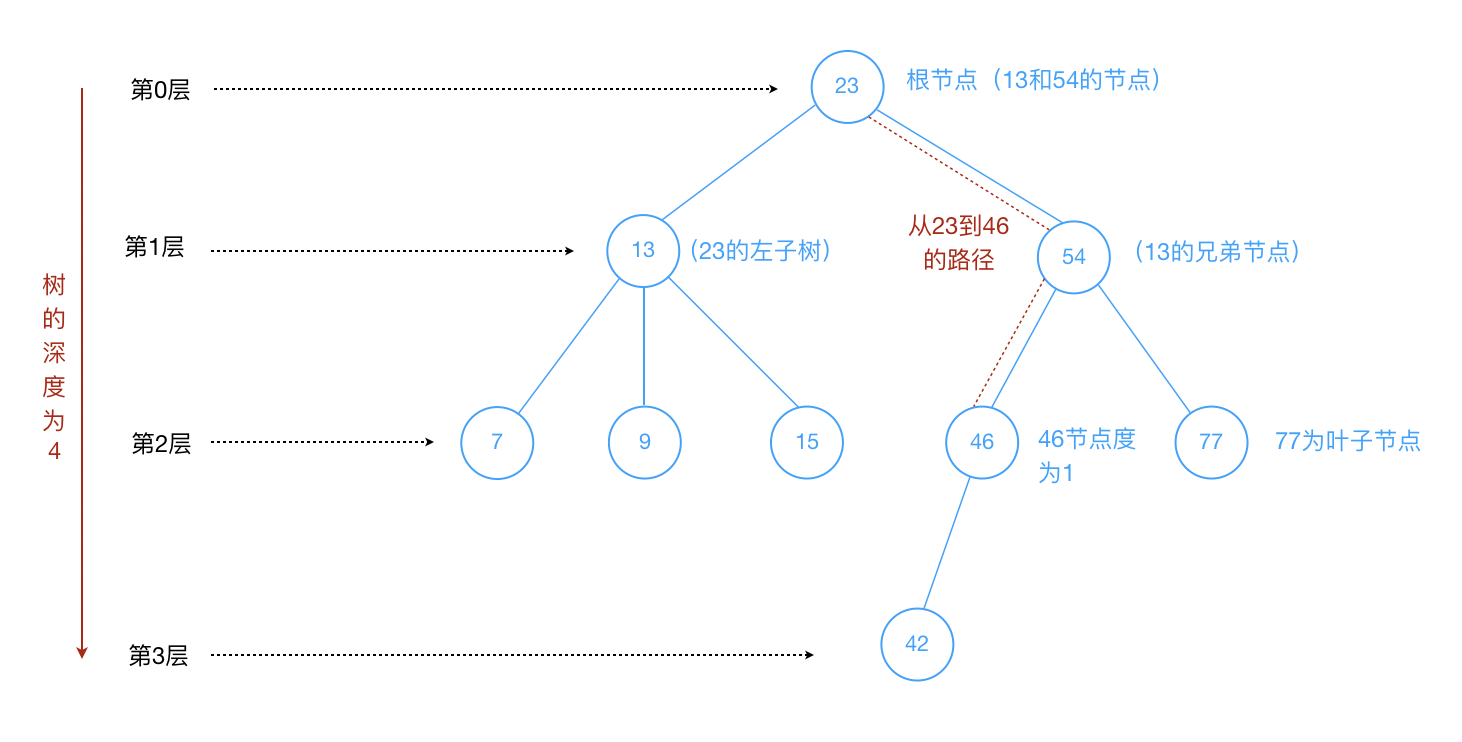
    - 路径和路径长度：从节点n1到nk的路径为一个节点序列n1,n2,n3,...,nk，ni是ni+1的父节点。路径所包含边的个数为路径长度。
    - 节点的层次（Level）：规定根节点在第0层，它的子节点是第1层，子节点的子节点是第2层，以此类推。
    - 树的深度（Depth）：树中所有节点中的最大层次是这棵树的深度（因为上面是从第0层开始，深度 = 第最大层数 + 1）

　　　　（3）树的四种遍历方式：

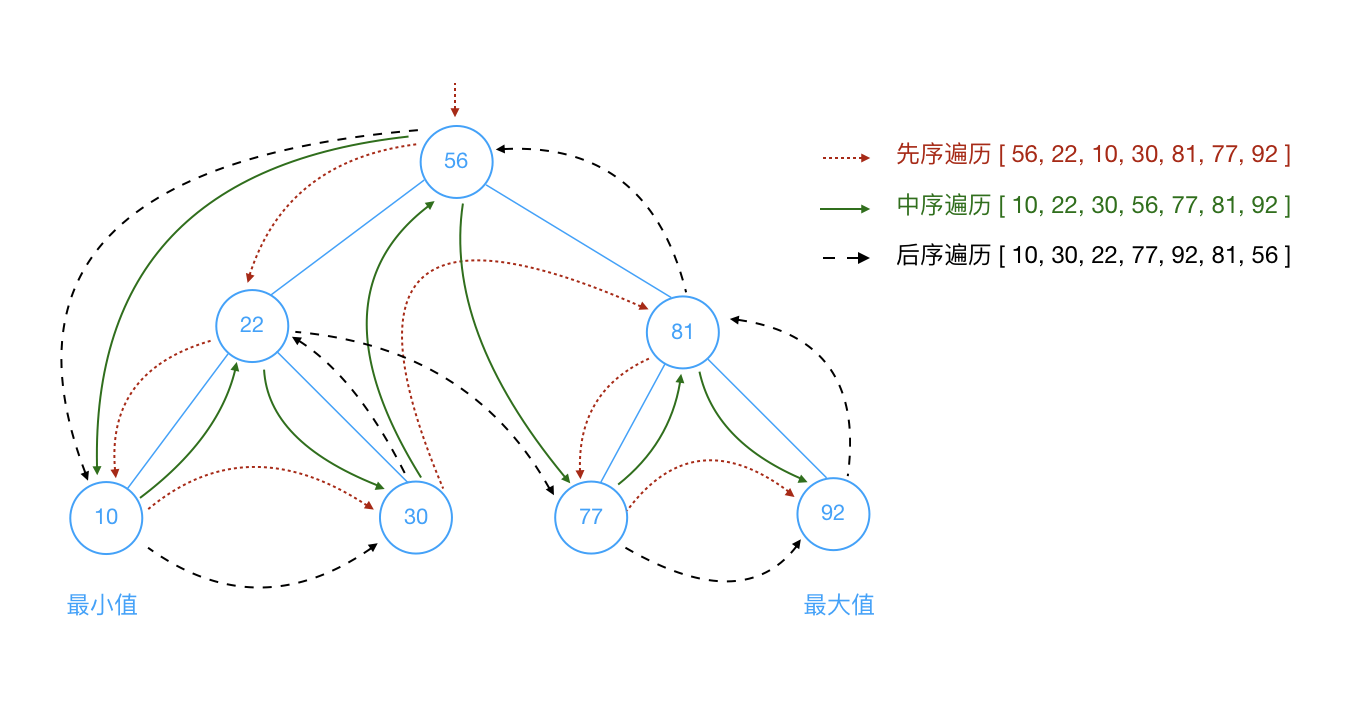
　　　　　　　　　　先序遍历、中序遍历、后序遍历、层次遍历。

　　　　　　　　　　前三种遍历方式都是以根的遍历先后为基准，层次遍历就比较简单了，按深度层次遍历，不再赘述。先中后序遍历做了一张图，可以用下面这张图来清晰解释：

二、树的重中之重——二叉树：

　　（1）二叉树的性质：

　　　　　　二叉树的每个结点至多有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。

　　　　　　① 在二叉树的第K层上，最多有 2k-1 (K >= 1）个结点
　　　　　　② 深度为K的二叉树，最多有 2k - 1 个结点（K>=1）
　　　　　　③ 对于任何一棵二叉树，如果其叶子结点的个数为K，度为2的结点数为M,则K=M+1
　　　　　　④ 对于一棵有 n 个结点的完全二叉树的结点按层次进行编号（如上图，从第一层到第（log 2n 向下取整），每层从左到右），对任意结点 i （1<i<n）,有：
　　　　　　　　→如果i=1，则结点i无父结点，是二叉树的根，如果i>1,则父结点为 i/2 向下取整
　　　　　　　　→如果2i>n,则结点i为叶子结点，无左子结点，否则，其左子结点为2i
　　　　　　　　→如果2i+1>n，则结点i无右子结点，否则，其右子结点是结点2i+1

　　（2）二叉树的存储结构表示方法：

　　　　　　① 孩子表示法：用指针指出每个节点的孩子节点

　　　　　　　　#优点：寻找一个节点的孩子节点比较方便。

　　　　　　　　#缺点：寻找一个节点得双亲节点很不方便。

　　　　　　② 双亲表示法：用指针表示出每个节点的双亲节点

　　　　　　　　#优点：寻找一个节点得双亲节点操作实现很方便

　　　　　　　　#缺点：寻找一个节点的孩子节点很不方便

　　　　　　③ 孩子双亲表示法：用指针既表示出每个节点得双亲节点，也表示出每个节点的孩子节点

　　　　　　　　#优点：找某个节点的双亲节点和孩子节点非常方便

　　　　　　④ 孩子兄弟表示法：即表示出每个节点的第一个孩子节点，也表示出每个节点的下一个兄弟节点

　　　　　　　　#优点：找某个节点的兄弟结点节点和孩子节点非常方便

　　（3）二叉树的基本建立与使用：

　　　　　　此处应用老师作业1的编程例题进行讲解——List Leaves

　　　　　　题目：

Given a tree, you are supposed to list all the leaves in the order of top down, and left to right.

Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤10) which is the total number of nodes in the tree -- and hence the nodes are numbered from 0 to N−1. Then N lines follow, each corresponds to a node, and gives the indices of the left and right children of the node. If the child does not exist, a "-" will be put at the position. Any pair of children are separated by a space.

Output Specification:
For each test case, print in one line all the leaves' indices in the order of top down, and left to right. There must be exactly one space between any adjacent numbers, and no extra space at the end of the line.

Sample Input:
8
1 -
- -
0 -
2 7
- -
- -
5 -
4 6
Sample Output:
4 1 5

7-1 List Leaves (30 分)题目

　　　　　　①首先：二叉树的基本数据结构的建立

　　　　　　　　对于树的建立，主要以打包结构体来实现，可打包加入左右孩子、数据data、编号等，这里以最简单的只保留左右孩子编号的结构体进行初涉讲解。

struct BiTree{
    int l;
    int r;
};

　　　　　　②其次：建树，找出根节点编号返回

int buildTree(BiTree tree[])
{
    //标记节点是否出现 
    bool number[MAX] = {false};
    
    //输入节点数 
    int times;
    scanf("%d",&times);
    
    //存储节点 
    for(int i = 0;i<times;i++)
    {
        char a,b;
        int Ta,Tb;
        getchar();
        scanf("%c %c",&a,&b);
        Ta = changeLegal(a);
        Tb = changeLegal(b);
         tree[i].l = Ta;
         tree[i].r = Tb;
         number[Ta] = true;
        number[Tb] = true;    
    }
    
    //搜索根节点 
    for(int i = 0;i<times;i++)
        if(number[i] == false)
            return i;
}

　　　　　　③对简单二叉树的应用：实现本题目的要求——找叶子节点

void findLeaves(BiTree tree[],int rt)
{
    //输出空格标记 
    int mark = 0;
    
    //申请队列并让根节点入队 
    queue<int> temp;
    temp.push(rt);
    
    //队列循环 
    while(!temp.empty())
    {
        //输出队列出队首个元素 
        int T = temp.front();
        temp.pop();
        
        //节点入队 
        if(tree[T].l!=-1) temp.push(tree[T].l);
        if(tree[T].r!=-1) temp.push(tree[T].r);
        //如果搜到左右孩子都是空的，那就是叶子节点了 直接输出即可 因为是层序遍历 
        if(tree[T].l == -1 && tree[T].r == -1) 
        {
            if(mark == 0)
            {
                printf("%d",T);
                mark = 1;
            }
            else printf(" %d",T);
        }
    }
}

　　　　　　完整代码展示：

#include<stdio.h>
#include<queue> 
#define MAX 11
using namespace std;

//结构体树节点建立 
struct BiTree{
    int l;
    int r;
};

//函数原型声明 
int buildTree(BiTree tree[]);
void findLeaves(BiTree tree[],int rt);

int main()
{
    //建立基于数组的树 
    BiTree tree[MAX];
    //存储树节点并识别根节点 
    int root = buildTree(tree);
    //搜索叶子节点并输出 
    findLeaves(tree,root);
    return 0;
}

//转换输入的内容，将char类型转为int 
int changeLegal(char x)
{
    if(x == '-') return -1;
    else return x - '0';
}

int buildTree(BiTree tree[])
{
    //标记节点是否出现 
    bool number[MAX] = {false};
    
    //输入节点数 
    int times;
    scanf("%d",&times);
    
    //存储节点 
    for(int i = 0;i<times;i++)
    {
        char a,b;
        int Ta,Tb;
        getchar();
        scanf("%c %c",&a,&b);
        Ta = changeLegal(a);
        Tb = changeLegal(b);
         tree[i].l = Ta;
         tree[i].r = Tb;
         number[Ta] = true;
        number[Tb] = true;    
    }
    
    //搜索根节点 
    for(int i = 0;i<times;i++)
        if(number[i] == false)
            return i;
}
 
void findLeaves(BiTree tree[],int rt)
{
    //输出空格标记 
    int mark = 0;
    
    //申请队列并让根节点入队 
    queue<int> temp;
    temp.push(rt);
    
    //队列循环 
    while(!temp.empty())
    {
        //输出队列出队首个元素 
        int T = temp.front();
        temp.pop();
        
        //节点入队 
        if(tree[T].l!=-1) temp.push(tree[T].l);
        if(tree[T].r!=-1) temp.push(tree[T].r);
        //如果搜到左右孩子都是空的，那就是叶子节点了 直接输出即可 因为是层序遍历 
        if(tree[T].l == -1 && tree[T].r == -1) 
        {
            if(mark == 0)
            {
                printf("%d",T);
                mark = 1;
            }
            else printf(" %d",T);
        }
    }
}

本题作者答案写法

三、树的升级拓展之一：哈夫曼树：

　　（1）定义：

　　　　　　哈夫曼树，又称最优树，是一类带权路径长度最短的树。首先有几个概念需要清楚：

　　　　　　1、路径和路径长度

　　　　　　从树中一个结点到另一个结点之间的分支构成两个结点的路径，路径上的分支数目叫做路径长度。树的路径长度是从树根到每一个结点的路径长度之和。

　　　　　　2、带权路径长度

　　　　　　结点的带权路径长度为从该结点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和，通常记作WPL。

　　　　　　若有n个权值为w1,w2,...,wn的结点构成一棵有n个叶子结点的二叉树，则树的带权路径最小的二叉树叫做哈夫曼树或最优二叉树。

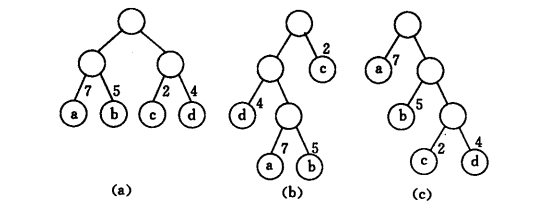
　　　　　　在上图中，3棵二叉树都有4个叶子结点a、b、c、d，分别带权7、5、2、4，则它们的带权路径长度为

　　　　　　（a）WPL = 7*2 + 5*2 + 2*2 + 4*2 = 36

　　　　　　（b）WPL = 4*2 + 7*3 + 5*3 + 2*1 = 46

　　　　　　（c）WPL = 7*1 + 5*2 + 2*3 + 4*3 = 35

　　　　　　其中（c）的WPL最小，可以验证，（c）恰为哈夫曼树。

　　（2）创建哈夫曼树：

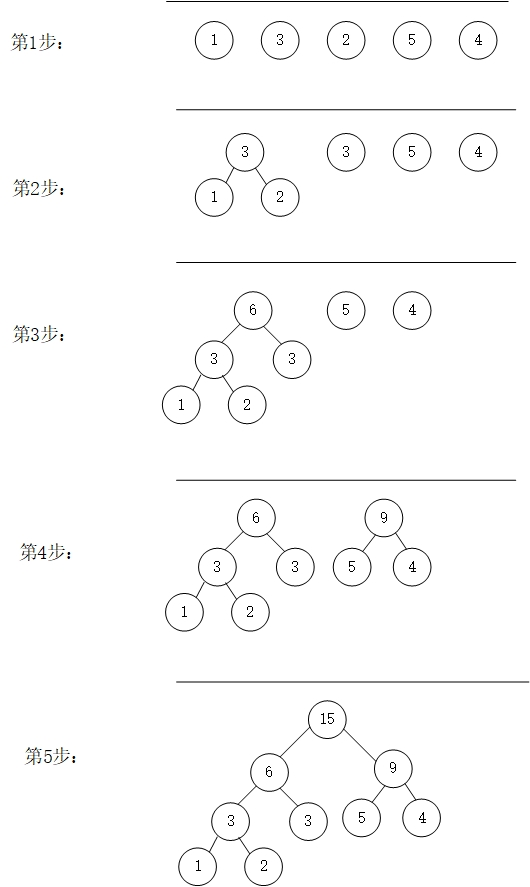
　　　　　　假设有n个结点，n个结点的权值分别为w1,w2,...,wn，构成的二叉树的集合为F={T1,T2,...,Tn}，则可构造一棵含有n个叶子结点的哈夫曼树。步骤如下：

　　　　　　（1）从F中选取两棵根结点权值最小的树作为左右子树构造一棵新的二叉树，其新的二叉树的权值为其左右子树根结点权值之和；

　　　　　　（2）从F中删除上一步选取的两棵二叉树，将新构造的树放到F中；

　　　　　　（3）重复（1）（2），直到F只含一棵树为止。

　　（3）哈夫曼编码：

　　　　　　我们约定左分支表示字符'0'，右分支表示字符'1'，在哈夫曼树中从根结点开始，到叶子结点的路径上分支字符组成的字符串为该叶子结点的哈夫曼编码。上面代码所创建的哈夫曼树如下所示：

　　　　　　可以看出3被编码为00，1为010，2为011,4为10,5为11。在这些编码中，任何一个字符的编码均不是另一个字符编码的前缀。

　　　注：因本内容在本学期要求仅理解创建过程和哈夫曼编码即可，故具体代码实现暂未总结。

四、本章习题练习：

　　　　（1）深入虎穴：

深入虎穴 (30 分)
著名的王牌间谍 007 需要执行一次任务，获取敌方的机密情报。已知情报藏在一个地下迷宫里，迷宫只有一个入口，里面有很多条通路，每条路通向一扇门。每一扇门背后或者是一个房间，或者又有很多条路，同样是每条路通向一扇门…… 他的手里有一张表格，是其他间谍帮他收集到的情报，他们记下了每扇门的编号，以及这扇门背后的每一条通路所到达的门的编号。007 发现不存在两条路通向同一扇门。

内线告诉他，情报就藏在迷宫的最深处。但是这个迷宫太大了，他需要你的帮助 —— 请编程帮他找出距离入口最远的那扇门。

输入格式：
输入首先在一行中给出正整数 N（<10
5
 ），是门的数量。最后 N 行，第 i 行（1≤i≤N）按以下格式描述编号为 i 的那扇门背后能通向的门：

K D[1] D[2] ... D[K]
其中 K 是通道的数量，其后是每扇门的编号。

输出格式：
在一行中输出距离入口最远的那扇门的编号。题目保证这样的结果是唯一的。

输入样例：
13
3 2 3 4
2 5 6
1 7
1 8
1 9
0
2 11 10
1 13
0
0
1 12
0
0
输出样例：
12

深入虎穴-题目

　　　　　　　　简单级难度，理清思路一个dfs就搞定了，关键部分：

void dfs(int rt,int step)
{
    if(step>step_max) {
        ans=rt;
        step_max=step;
    }
    for(int i=0;i<E[rt].size();++i){
        int to=E[rt][i];
        dfs(to,step+1);
    }    
}

　　　　　　　　完整代码展示：干净整洁

#include <iostream>
#include <queue>
#include <stdio.h>
#include <vector>
using namespace std;
const int maxn = 1e5+10;
queue<int>q;
vector<int>E[maxn];
int N,to,ans=0,step_max=0;
void dfs(int rt,int step)
{
    if(step>step_max) {
        ans=rt;
        step_max=step;
    }
    for(int i=0;i<E[rt].size();++i){
        int to=E[rt][i];
        dfs(to,step+1);
    }    
}
int main()
{
    int step=1;
    scanf("%d",&N);
    for(int i=1;i<=N;++i){
        int num;
        scanf("%d",&num);
        while(num--)
        {
            scanf("%d",&to);
            E[i].push_back(to);
        }
    }
    dfs(1,1);
    printf("%d",ans);
    return 0;
}

　　（2）树的同构：

树的同构 (30 分)
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。
图1
图2
现给定两棵树，请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:
如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
输出样例1:
Yes
输入样例2（对应图2）：
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
输出样例2:
No

树的同构 - 题目

　　　　　　本题的难度主要在于如何判断两个树是否同构，一开始给自己挖坑了，想用迭代法去写，结果发现越写越复杂，后来换了一种骚递归的方法居然发现是如此的简单，把握好老师说的：停留在本层的方法，一切就很容易了。

　　　　　　①首先：搜索到当前的节点没有孩子，即自己是叶子，那他的两个孩子一定是判为相等的，true返回

　　　　　　②其次：如果当前节点两边都有孩子，并且当前两棵树的孩子一样，那么就继续往下搜，并且搜索有四种方向：

　　　　　　　　A树左孩子与B树左孩子、A树左孩子与B树右孩子、A树右孩子与B树左孩子、A树右孩子与B树右孩子

　　　　　　因此关键的判定函数就可以写出来了：

//judge function
bool isEqual(Tree *a,int root_a,Tree *b,int root_b)
{
    if(root_a == -1 && root_b == -1)
        return true;
        
    if((root_a != -1 && root_b !=-1))
        if(a[root_a].name == b[root_b].name)
        {
            if(isEqual(a,a[root_a].lchild,b,b[root_b].lchild) && isEqual(a,a[root_a].rchild,b,b[root_b].rchild))
                return true;
            if(isEqual(a,a[root_a].lchild,b,b[root_b].rchild) && isEqual(a,a[root_a].rchild,b,b[root_b].lchild))
                return true;
        }
    return false;
}

　　　　　　完整代码展示：（时刻提醒自己模块化书写）

#include<stdio.h>

//define Node
typedef struct{
    char name;
    int lchild;
    int rchild;
}Tree;

//define variable
int times1,times2;

//define function
int buildTree(Tree *&t,int node);
bool isEqual(Tree *a,int root_a,Tree *b,int root_b);

//MAIN
int main()
{
    //create Tree
    Tree *a,*b;
    
    //build Tree
    scanf("%d",&times1);
    int root_a = buildTree(a,times1);
    scanf("%d",&times2);
    int root_b = buildTree(b,times2);
    
    //find equal Tree
    if(isEqual(a,root_a,b,root_b)) printf("Yes");
    else printf("No");
    
    return 0;
}

//build Tree Function
int buildTree(Tree *&t,int node)
{
    t = new Tree[node];
    bool* mark = new bool[node];
    for(int i = 0;i<node;i++) mark[i] = false;
    for(int i = 0;i<node;i++)
    {
        //Warning!↓ 
        getchar();
        //Warning!↑
         
        char temp_n,temp_l,temp_r;
        scanf("%c %c %c",&temp_n,&temp_l,&temp_r);
        t[i].name = temp_n;
        if(temp_l != '-') 
        {
            t[i].lchild = temp_l - '0';
            mark[temp_l - '0'] = true;
        }
        else t[i].lchild = -1;
        if(temp_r != '-') 
        {
            t[i].rchild = temp_r - '0';
            mark[temp_r - '0'] = true;
        }
        else t[i].rchild = -1;
    }
    for(int i = 0;i<node;i++)
        if(mark[i] != true)
            return i;
    return -1;
}

//judge function
bool isEqual(Tree *a,int root_a,Tree *b,int root_b)
{
    if(root_a == -1 && root_b == -1)
        return true;
        
    if((root_a != -1 && root_b !=-1))
        if(a[root_a].name == b[root_b].name)
        {
            if(isEqual(a,a[root_a].lchild,b,b[root_b].lchild) && isEqual(a,a[root_a].rchild,b,b[root_b].rchild))
                return true;
            if(isEqual(a,a[root_a].lchild,b,b[root_b].rchild) && isEqual(a,a[root_a].rchild,b,b[root_b].lchild))
                return true;
        }
    return false;
}

五、个人反思及未来计划：

　　　　（1）对树和图比较抽象的数据结构上基础有些不牢，特别是碰到链式存储的指针使用的时候，需要找时间给自己多加强这方面的学习。

　　　　（2）2019年5月12日即将参加CCPC广东省ACM省赛，在此之前熟练学习『BFS』『DFS』『双搜』『启发式搜索』『A*』『迭代加深搜索』『IDA*』『回溯法』

　　　　（3）为树蛙预备队员转型树蛙正式成员准备复习高数以及Python　　　　

　　　　（4）完成论文标解『Improving patch-based scene text script identification with ensembles of conjoined networks』

posted @ 2019-05-04 14:52 嗨威er 阅读(366) 评论(5) 编辑收藏举报

刷新页面返回顶部

嗨威er

『嗨威说』数据结构 - 第五章学习内容小结

一、树的基本概念：

（1）树的定义：

（2）树的基本术语：

（3）树的四种遍历方式：

二、树的重中之重——二叉树：

（1）二叉树的性质：

（2）二叉树的存储结构表示方法：

（3）二叉树的基本建立与使用：

三、树的升级拓展之一：哈夫曼树：

（1）定义：

（2）创建哈夫曼树：

（3）哈夫曼编码：

四、本章习题练习：

（1）深入虎穴：

（2）树的同构：

五、个人反思及未来计划：

公告

　　　　（1）树的定义：

　　　　（2）树的基本术语：

　　　　（3）树的四种遍历方式：

　　（1）二叉树的性质：

　　（2）二叉树的存储结构表示方法：

　　（3）二叉树的基本建立与使用：

　　（1）定义：

　　（2）创建哈夫曼树：

　　（3）哈夫曼编码：

　　　　（1）深入虎穴：

　　（2）树的同构：