快速排序算法

　　对于包含n个数的输入数组来说，快速排序是一种最坏情况时间复杂度为θ(n²)的排序算法。虽然最坏情况时间复杂度很差，但是快速排序通常是实际排序应用中最好的选择，因为它的平均性能非常好：期望时间复杂度是θ(nlgn)，且θ(nlgn)中隐含的常数因子非常小。

 ① 分解：数组A[p..r]被划分为两个（可能为空）子数组A[p..q-1]和A[q+1..r]，使得A[p..q-1]中的每一个元素都小于等于A[q]，而A[q]也小于等于A[q+1..r]中的每个元素。其中，计算下标q也是划分过程的一部分。

② 解决：对子数组A[p..q-1]和A[q+1..r]递归的调用快速排序。

③ 合并：因为子数组都是原址排序的，所以不需要合并操作，此时的A数组已经有序。

　　第一种写法

---

    　【注】详情参见《算法导论》第3版第96页

　　   伪代码如下：

　　 QUICKSORT(A,p,r)

if p<r
    q = PARTITION(A,p,r)
    QUCIKSORT(A,p,q-1)
    QUICKSORT(A,q+1,r)

　　 PARTITION(A,p,r)

x = A[r]
i = p-1
for j=p to r-1
    if A[j]≤x
        i = i + 1
        exchange A[i] with A[j]
exchange A[i+1] with A[r]
return i+1

　　具体工作过程如图1所示：

　　

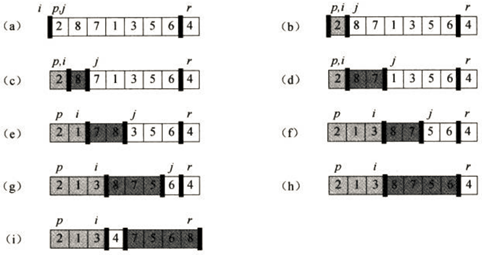
　　 图1：在一个样例数组上的PARTITION过程。数组项A[r]是主元x。

　　Python实现代码：

def quicksort(ar, p, r):
    if p < r:
        q = partition(ar, p, r)
        quicksort(ar, p, q - 1)
        quicksort(ar, q + 1, r)
    else:
        return


def partition(ar, p, r):
    x = ar[r]
    i = p-1
    for j in range(p, r):
        if ar[j] <= x:
            i = i + 1
            ar[i], ar[j] = ar[j], ar[i]
    ar[i+1], ar[r] = ar[r], ar[i+1]
    print ar
    return i+1


arr = [2, 8, 7, 1, 3, 5, 6, 4]
print "initial array:\n", arr
print "***************************"
quicksort(arr, 0, len(arr) - 1)
print "***************************"
print "result array:\n", arr

 

　　第二种写法

---

　　【注】详情参见《算法设计与分析（第2版）》屈婉玲、刘田等编著 清华大学出版社 第37页

 　　伪代码如下：

 　　Quicksoft(A,p,r)

if p<r
then q←Partition(A, p, q-1) //划分数组，找到首元素A[p]在排好序后的位置q
     A[p]←→A[q]
     Quicksort(A, p, q-1)
     Quicksort(A,q+1,r)

　　Partition(A,p,r)

x←A[p]
i←p
j←r+1
while true do
    repeat j←j-1
    util A[j]≤x
    repeat i←i+1
    until A[i]>x
    if i < j
     then A[i]←→A[j]
     else return j

 

　　划分过程如图2所示：

　　

　　　图2 划分过程

　　　Python实现代码：

def quicksort(ar, p, r):
    if p < r:
        q = partition(ar, p, r)
        arr[p], arr[q] = ar[q], arr[p]
        quicksort(ar, p, q - 1)
        quicksort(ar, q + 1, r)
    else:
        return


def partition(ar, p, r):
    x = ar[p]
    i = p
    j = r
    while 1:
        while ar[j] > x:
            j = j - 1
        while i <= r and ar[i] <= x:　#不可调换顺序。加入i<=r这个条件是为了防止“A[p]为最大数”时出现A[r+1]越界的情况
            i = i + 1
        if i < j:
            ar[i], ar[j] = ar[j], ar[i]
        else:
            return j


arr = [65, 56, 72, 99, 86, 25, 34, 66]

print "initial array:\n", arr
quicksort(arr, 0, len(arr) - 1)
print "result array:\n", arr

　　利用Python的特性，更为简单的实现代码如下：

x=[166,13,51,76,81,26,57,69,23]

def qs(array):
    if len(array)<2:
        return array
    else:
        f = array[0]
        left = [i for i in array[1:] if i <= f]
        right = [j for j in array[1:] if j >= f]
        return qs(left) + [f] + qs(right)
    
print qs(x)

 

快速排序算法性能分析

---

 　　快速排序的运行时间是跟划分密切相关的，因为划分影响着子问题的规模。

　　(1) 最坏情况划分

    当每次划分把问题分解为一个规模为n-1的问题和一个规模为0的问题时，快速排序将产生最坏的情况（以后给出这个结论的证明，目前可以想象的出）。由于划分操作的时间复杂度为θ(n)；当对一个长度为0的数组进行递归操作时，会直接返回，时间为T(0) = θ(1)。于是算法总运行时间的递归式为：

T(n) = T(n-1) + T(0) + θ(n) = T(n-1) + θ(n) 。

　　可以解得，T(n) = θ(n²)。

    由此可见，在划分都是最大程度不平均的情况下，快速排序算法的运行时间并不比插入排序好，甚至在某些情况下（比如数组本身已按大小排好序），不如插入排序。

　　(2) 最好情况划分

    当每次划分都是最平均的时候（即问题规模被划分为[n/2]和[n/2]-1时），快速排序性能很好，总运行时间的递归式为：

T(n) = 2T(n/2) + θ(n)

　　可以解得，T(n) = θ(nlg n)。

 

　　(3) 平均划分

    快速排序算法的平均运行时间，更接近于最好情况划分时间而非最坏情况划分时间。理解这一点的关键就是理解划分的平均性是如何反映到描述运行时间的递归式上的。

    我们举个例子，对于一个9:1的划分，乍一看，这种划分是很不平均的。此时的运行时间递归式为：

T(n)  = T(9n/10) + T(n/10) + cn，

 　 可以用如下递归树来更加形象地描述运行时间：

　　

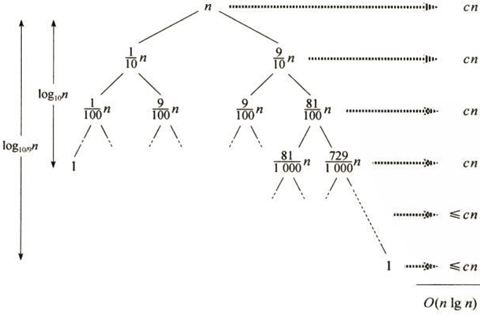
　　递归会在深度为log10/9n = θ(lg n )处终止，因此，快速排序的总代价为O(nlgn)。可见，在直观上看起来非常不平均的划分，其运行时间是接近最好情况划分的时间的。事实上，对于任何一种常数比例的划分，其运行时间总是O(nlgn)。