泰勒级数&傅立叶级数(通信层面)
(#977)
泰勒级数的基本公式.
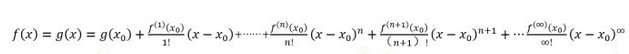
这个方程相当于是待解析曲线在求解点附近做了一条切线,并进行迭代法累加(n阶导数)。迭代次数越多,越接近原始曲线。举例用泰勒级数来分解sin(t),相当于把一个光滑的函数(三角函数)变成一些列有楞有角的波形的叠加.
而n阶导数可以理解为不同的相互独立的维. 相互之间是天然的正交关系. (这个需要专业证明啊).
傅立叶级数的基本公式
![]()
这个方程相当于是待解析周期曲线用n阶三角函数进行累加, 用傅立叶级数表达周期方波, 相当于把一个有棱有角的曲线变成一些光滑的波形的叠加(不总是如此,因为也可以是光滑的周期曲线). sin(nx),cos(nx)的正交关系是LZ在之前的连载中早就说明了的.
两者之间实际上还是有很大区别的. 泰勒级数主要作用是将不可计算的无理数对象分解为若干的可计算的有机数对象, 其性能考察包括收敛性. 收敛性越好,计算效率就越高(不需要太多逼近就能够计算出足够精度的结果)
而傅立叶级数主要是针对周期信号的(傅立叶变换是假设周期T为无穷大,引申出来的,不在此讨论),
且用三角函数进行分解.高收敛性肯定不是评价其性能的标尺.
通过欧拉公式及e常数(e常数的一个主要特点是其导数特性,太特别了(e^x)'=e^x), 可以正如LZ所讲解的那样,
傅立叶级数将周期信号分解成若干的旋转向量. 将指数运算变成乘积运算及相位的相加运算.
更深刻的只能期待数学专家的出场了!
(#1840)
所谓正交是指两个信号,经过乘法和[-T/2,T/2]的积分运算之后,结果为零。以物理的观点来看,正交的两个信号是不相关的。
我们也可以把乘法和[-T/2,T/2]的积分运算定义为相关运算,任何两个信号,经相关运算后不为零,说明他们互相关,否则为不相关。
同一个信号分成两路,其中一路经过时延后再与另一路作相关运算,得到的结果如果越大,则自相关性越好,否则就是自相关性越差。自相关性体现了信号随时间变化的随机性。可以想象,对随机码作自相关运算(时延不为零),结果为零。
相关性放到光频中,就是相干性。大家可以回顾一下大学做双缝衍射实验的时候,条纹可见度与两个狭缝距离、光源特性的关系。
(#2965)
对于周期函数用的傅里叶级数展开,求得傅里叶系数,即得到线频谱。系数Cn的长度(高度)随频率增加而逐渐减小
而当周期函数的周期慢慢增大时,系数的长度相对于原来也逐渐减小,
当周期无限增大时,系数Cn高度趋于无限小,而其实在各个频率分量之间它的高度仍有差异
此时我们将每个系数都除以一个无穷小,即△f.然后用这种相对高度去刻画这种分布的趋势
从而将其定义为频率密度。
自己想的时候觉得太巧合了,为什么刚好在求Cn的积分表达的式的右端刚好有一个1/T,即△f(无穷小),然后得到Cn/△f(即频谱密度)
通信行业做研发需要哪些技能,和具体做的工作有关。如果你做软件开发,一般要求掌握C语言;你做硬件开发,一般要求掌握单片机/DSP相关电路设计、原理图编辑工具等;如果你做预研,对matlab/Simulink等仿真工具的要求就比较高;如果你做基站基带、中射频部分的开发,对通信原理的要求就比较高。等等。虽然都是在通信行业做研发,要求掌握的技能差别还是挺大的。
对于多径效应,OFDM和CDMA采用了完全不同的四路来解决:
OFDM将高速的串行码流转换为低速的并行码流,同时利用循环前缀消除多径引起的码间串扰和子载波间干扰;
CDMA通过扩频将低速的码流转换为高速的码流,同时利用Rake接收技术对多径信号进行接收和合并,变害为利。
Ref: http://www.txrjy.com/thread-394879-49-1.htm
傅里叶变换交互式入门:http://www.jezzamon.com/fourier/zh-cn.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号