深入浅出通信原理连载145-389(Python代码版)
深入浅出通信原理Python代码版
本文跨度比较大,因为项目需求突然催的紧了,所以草草了事,有空再详细补充说明吧
深入浅出通信原理是陈爱军的心血之作,于通信人家园连载,此处仅作python代码笔记训练所用
陈老师的连载从多项式乘法讲起,一步一步引出卷积、傅立叶级数展开、旋转向量、三维频谱、IQ调制、数字调制等一系列通信原理知识
采样详解
模/数转换(ADC)
模拟信号f(t) -- 采用抽样脉冲p(t) --> 抽样信号f_s(t) -- 量化编码 --->数字信号f[n]
(ADC内部结构----连载149)
理想抽样
时域上->模拟信号与抽样脉冲相乘得到抽样信号:\(f(t)p(t)=f_s(t)\)
频域上->模拟信号傅里叶变换与抽样信号傅里叶变换卷积的结果
抽样脉冲\(p(t)=\sum_{n=-\infin}^{+\infin}\delta(t-nT_s)\)
抽样脉冲频域\(F[p(t)]=\sum_{k=-\infty}^{+\infty}2\pi c_k\delta(w-kw_0)=\frac{2\pi}{T_s}\sum_{k=-\infty}^{+\infty}\delta(w-kw_0)\)
抽样脉冲频谱密度是一系列间隔为\(\omega_0=\frac{2\pi}{T_s}\)的强度为\(\frac{2\pi}{T_s}\)的冲激信号
因此在时域进行抽样,即在频域以采样频率为间隔对频谱作周期性延拓
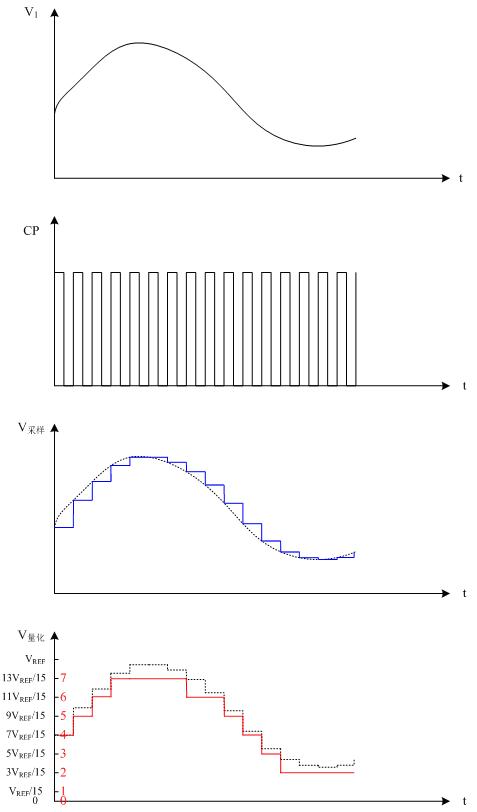
平顶采样
采样输出\(V_{采样}=f_s(t)=f(nT_s)\neq f(t)p(t)\)
平顶采样=理想采样+脉冲成型滤波器(连载152)
脉冲成型滤波器:
输入理想脉冲 \(x(t)=f(t)p(t)=\sum_{n=-\infty}^{+\infty}f(nT_s)\delta(t-nT_s)\)
输出平顶采样 \(y(t)=x(t)*h(t)=\sum_{n=-\infty}^{+\infty}f(nT_s)h(t-nT_s)\)
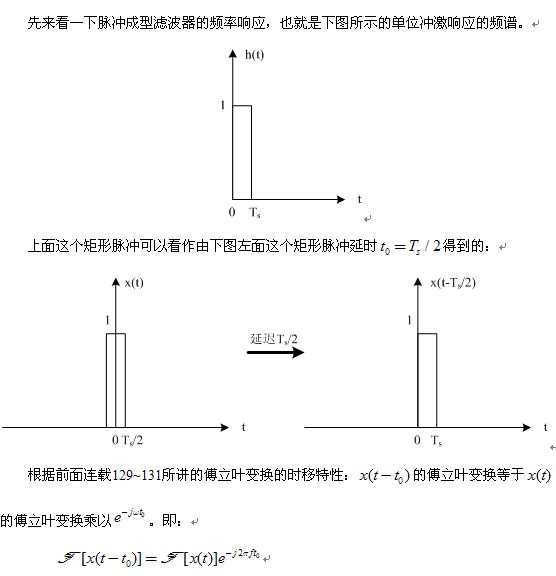
脉冲成型滤波器的单位冲激响应的傅里叶变换称为脉冲成型滤波器的频率响应
频率响应\(T_s sinc(T_sf)\)=幅频响应+相频响应
# 脉冲程序滤波器的频率响应|H(f)|=Ts*|sinc(Ts*f)| f=np.arange(-30,30.1,0.1) Ts=0.1 y=abs(Ts*np.sinc(Ts*f)) plt.plot(f,y) plt.title("脉冲信号幅频响应",fontproperties='stsong') plt.show()
平顶采样信号恢复
(连载180)
由于通过频率响应是H(f)的脉冲成型滤波器可得平顶抽样信号频谱,因此接收端也通过1/H(f)的滤波器即可得到理想抽样信号频谱,再通过理想低通滤波器即可恢复原模拟信号
若没通过频率响应是1/H(f)的滤波器,会造成孔径失真的现象
采样用途
PCM系统(连载160):
语音信号以8kHz采样,每个采样值进行量化编码成8bit,传输一路语音信号需64kbps
奈奎斯特采样定理
从 抽样信号中无失真恢复原信号,抽样频率需要大于2倍信号最高频率
对 频率kfs+f的余弦信号进行采样频率fs的采样,恢复出频率f的余弦信号(连载164、165)
因为DAC通常选择接近零频的混淆频率转换成模拟信号
折叠频率
把采样频率的一半(fs/2)称为折叠频率,因为频率高于fs/2低于-fs/2都会折叠到区间[-fs/2, fs/2]
因此采用抗混叠滤波器(低通滤波器通带[-fs/2, fs/2])将区间外的信号滤去防止混叠
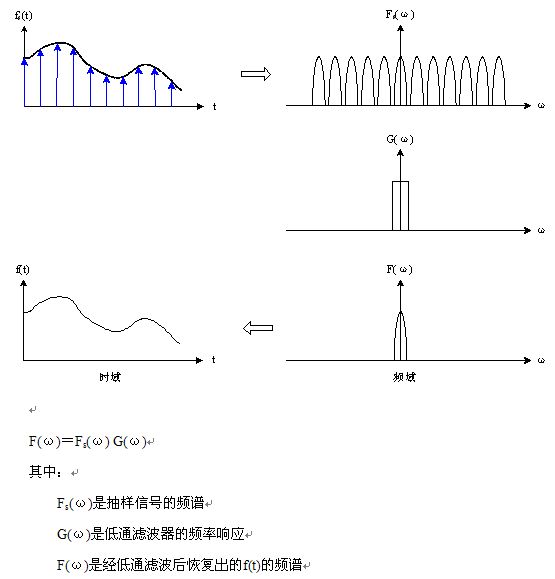
频域理解采样恢复信号:
在时域进行抽样,即在频域以采样频率为间隔对频谱作周期性延拓,即得到抽样信号后进行傅里叶变换,再通过低通滤波器将周期延拓后的频谱的一个周期取出,再进行逆傅里叶变换即可
时域理解采样恢复信号:
抽样信号卷积sinc信号(低通滤波器的单位冲激响应)所得即原始模拟信号
抽样信号的多个冲激以抽样时间间隔依次送入低通滤波器,低通滤波器以抽样时间间隔输出多个sinc信号,其叠加结果是原始模拟信号
带通信号采样定理
(连载182)
中心频率是\(f_0\),带宽是B的带通信号,其截至频率分别是\(f_H=f_0+B/2\)和\(f_L=f_0-B/2\)
则采样频率应满足\(\frac{2f_H}{m}\leq f_s\leq \frac{2f_L}{m-1}\)
其中:m=1,2,...,max, max指的是不大于f_H/B的最大整数
当信号频率正好是带宽的整数倍时,其最低采样频率正好是带宽2倍,其余情况均大于2倍带宽
但是当信号最高频率远大于带宽时,只需要以略大于2倍带宽的采样频率进行采样即可
因此设计信号时往往将信号最高频率设计成带宽的整数倍(连载189)
由此需要抗混叠滤波器(带通滤波器通带带宽B)将所需频带外的信号滤除
要实现无码间串扰,所需的最小带宽只要码元速率的一半
通常情况下都取码元宽度为整数倍个载波周期,具体取多少取决于如下因素:
1、载波周期取决于你所用的频段和具体的中心频率,载波周期=1/中心频率。
2、码元宽度取决于你所用的带宽和脉冲成型滤波器。码元宽度=1/码元速率。根据奈奎斯特第一准则,码元速率最大不能超过基带带宽的两倍。如果是双边带调制,射频带宽等于基带带宽的2倍,也就是码元速率不能超过射频带宽。码元速率有最大值也就是意味着码元宽度存在最小值,码元宽度的最小值等于1/(2倍基带带宽),对于双边带调制来说就是1/射频带宽。
综上所述,码元宽度/载波周期>=中心频率/2倍基带带宽
对于双边带调制来讲,码元宽度/载波周期>=中心频率/射频带宽
相位相关
连载212、213:
相位失真——信号若要无失真通过延时系统,不同频率成分的相移必须与频率成正比
无失真延时系统的相频曲线应当是一条经过原点,斜率是-t0的直线
波的干涉:若频率相同相位差恒定且震动方向相同的波在媒介中相遇,则会在叠加区域某些位置震动持续加强(相长干涉),某些区域始终减弱甚至抵消(相消干涉)。
相干解调/非相干解调:接收机需要一个与发送载波同频同相的载波副本进行解调称相干解调,只需要同频的副本则称非相干解调
载波副本通过同步电路获取,同步电路核心是锁相环PLL(Phase-Locked Loop)
码间串扰相关
奈奎斯特第一准则:
在带宽是B的信道传送码元时,若想实现无码间串扰,码元速率R不大于两倍带宽。若使用奈奎斯特速率2B传输码元,必须使用带宽是B的理想低通滤波器对数据进行滤波。
因此基带系统单位频带利用率:\(\eta=R/B=2Band/Hz\)
但由于理想低通滤波器时域的单位冲激响应是sinc信号,衰减较慢,当时间同步不精确时易造成较大码间串扰,因此采用升余弦滚降滤波器
若以码元传输速率最大速率2B传输,升余弦滚降滤波器所需信道带宽是2B
# 连载221,222 升余弦滚降滤波器与理想低通滤波器频域频率响应与时域单位冲激响应对比 plt.subplot(2,1,1) f=np.arange(-1.0,1.01,0.01) x = [-1.5,-0.5,-0.5,0.5,1.5] y = [0,0,1,1,0] plt.plot(x,y,drawstyle='steps-pre',label='low_pass_filter') y2 = 0.5*(1+np.cos(np.pi*f)) plt.plot(f,y2,label='raised_cosine_FIR') plt.title('滤波器频率响应',fontproperties='stsong') plt.legend() plt.show() # 单位冲激响应,B=0.5 plt.subplot(2,1,2) t = np.arange(-4,4.01,0.01) y1 = np.sinc(t)*np.cos(np.pi*t)/(1-4*t*t) plt.plot(t,y1,color='r',label='raised_cosine_FIR') y2 = np.sinc(t) plt.plot(t,y2,label='low_pass_filter') plt.title('滤波器单位冲激响应',fontproperties='stsong') plt.legend() plt.plot() plt.tight_layout()
当滚降系数a=0时是理想低通滤波器,占用信道带宽最小,频带利用率最高,但易码间串扰
脉冲成型滤波器/基带滤波器(BBF):就是指升余弦滚降滤波器或者理想低通滤波器
若使用升余弦滚降滤波器,滚降系数是a,则基带带宽B=R(1+a)/2
基带带宽有基带信号速率与脉冲成型滤波器相关(连载231)
双边带调制的频带传输系统的频带带宽是基带带宽的2倍(连载233)
单边带调制是按照双边带调制方式调制但只发送一个边带,因此只占用一半带宽
OFDM系统只发送实部是两倍射频带宽,虚实部都发送是只发送实部下的一半带宽(连载268)
已调信号通过非线性功率放大器会失真,且失真程度与频带信号的包络起伏有关,包络起伏越大失真越大。
因为I(t)与Q(t)同时过零时信号包络\(\sqrt{I^2(t)+Q^2(t)}\)会过零,因此只需错开半个码元信号便不再过零,这便是OQPSK设计思想,从QPSK的非恒包络发展为OQPSK的恒包络,便于使用非线性功放。
IFFT后通过“加窗“来减小带外的拖尾之后进行上变频
数字调制方式是MPSK或MQAM,子载波数是N,则OFDM符号速率是串行比特速率的: \(1/Nlog_2M\)
OFDM调制方式只采用BPSK,QPSK,QAM等,不采用OQPSK
OFDM调制通过IFFT实现,解调通过FFT实现
基带信号、采样判决情况下的码间串扰(ISI)
相同多径时延的情况下,码元周期越长,采样时刻相对来说越靠后,多径效应影响越小,码间串扰可能性越小(连载283)
而增大码元周期的手段就是串并转换,将串行的高速码流(码元周期短)转换成多行并行的低速码流
增大码元周期减小多径效应干扰,而在码元之间加入保护间隔可彻底消除多径效应的干扰,保护间隔长度应当大于最大多径时延。
OFDM符号时长\(T_s\)取最低频率\(f_0\)载波的一个完整周期,即\(T_s=1/f_0=1/\Delta f\)
子载波间干扰(ICI)
加入保护间隔后子载波之间由于多径时延无法同步因此不再正交,子载波之间积分不是0,出现干扰
采用OFDM循环前缀的方式消除子载波间干扰,把OFDM符号最后部分搬移到保护间隔时间处
只要循环前缀(保护间隔)长度大于多径时延,不管有几个多径时延,均可以保证正交关系
时延越小的路径,距离越短,对应信号越强。而时延越大的径,对应信号越弱
CDMA通过扩频将低速码流转换成高速码流,同时利用Rake接受技术对多径信号进行接受和合并。
表面上是对整个信号作FFT,实际上要先以一定采样频率对信号进行采样再作FFT变换,采样频率一定,FFT得到的频谱一定是对应一段时间的时域信号
-->为什么时域的点数和频域的点数是相同的呢?
离散傅里叶变换的公式,当时域采样N个点,频域如果大于N则周期重复不需要了,小于N不能把所有频带都包进去。所以都是N
DFT变换的两个序列X(k)和x(n)的长度是相等的,都是N。
做数字变换的时候,总是讲这是两个序列,从一定程序上掩盖了两个序列的N究竟代表什么意思。
对于一个连续的时间信号,对其时域采样后,频域周期拓展,成为周期性的连续频谱形状。
对于这样一个周期性的连续频谱形状进行频域采样,时域发生周期拓展,成为周期而离散的时域形状。
至此,时域和频域都成为周期而离散的状态。分别取其一个主值区间,对应的变换关系就是DFT/IDFT。对于x(n),它来源于对一个有限长连续信号x(t),时长为T,以间隔为Ts的抽样信号对其进行采样,T时长内会产生N个样点,即N*Ts=T。由连续信号傅里叶变换的性质可以知道,采样后的离散信号的频域,其实是对原信号x(t)频域的周期扩展,频域中的一个周期长度F=1/Ts=N/T(以后形成频域主值区间)。
那么在频域内谱线的间隔f0是多少呢?原则可以随意定。根据傅里叶逆变换性质可知,频域采样间隔f0决定着时域信号周期扩展后一个周期的长度,即f0=1/Tp.
可见,只有在Tp>>T时,才会使周期拓展后的时域信号不发生重叠,对于Tp-T这段多出来的时间内,原信号为零,这就是常说的频域过采样时域补0。
反之,如果f0选择的值比较大,造成Tp=1/f0<<T,相当于对原有的信号发生了截短效应。
无论如何,现在时域内一个主值区间的长度是Tp了。频域内有多少个点呢?
频域宽度F=1/Ts=N/T, 频域采样间隔f0=1/Tp, Nf=F/f0=N*Tp/T.再来看时域,信号周期的长度由T扩展/压缩到Tp,那么Tp时长内会产生多少时域样点呢?Nt=Tp/Ts=Tp/(T/N)=N *Tp/T.
可见,Nt=Nf,即时域序列的点数和频域序列的点数总是相等的。
如果f0的选取使得Tp=T,即对原信号即不补0,也不截短,这时Nt=Nf=N。
连载361
当时域采样频率是fs时,频域周期性拓展的周期就是fs,N点DFT得到的就是以fs为周期的频谱的N个样本点,频域样点之间的频率间隔时fs/N
连载382
截断的过程又称“加窗”,加矩形窗时域信号突然被截断,因此旁瓣泄露较大,若加入缓变的窗函数,对数据进行缓慢阶段可实现减小旁瓣泄露的目的





 浙公网安备 33010602011771号
浙公网安备 33010602011771号