深入浅出通信原理连载75-95(Python代码版)
深入浅出通信原理Python代码版
目录
傅里叶变换与反变换
Fourier Transform:
\[X(f) = \int_{-\infty}^{+\infty}x(t)e^{-j2\pi ft}dt \\
X(\omega)= \int_{-\infty}^{+\infty}x(t)e^{-j\omega t}dt
\]
Fourier inverse Transform:
\[x(t)=\int_{-\infty}^{+\infty}X(f)e^{j2\pi ft}df
\]
傅里叶变换性质
| 时域 | 频域 |
|---|---|
| \(x(t)\) | \(X(\omega)\) |
| \(x(t)e^{j\omega_0t}\) | \(X(\omega-\omega_0)\) |
| \(x(t)e^{-j\omega_0t}\) | \(X(\omega+\omega_0)\) |
信号x(t)在时域乘上\(e^{j\omega_0t}\), 相当于频谱X(w)右移\(\omega_0\);信号在时域乘上\(e^{-j\omega_0t}\), 相当于频谱左移\(\omega_0\);
信号x(t)调制载波\(cos\omega_0t\), 相当于频谱X(w)一分为二并分别左移右移\(w_0\)
# coswt频谱搬移作用 x = np.arange(-np.pi/2,np.pi/2,0.01) y = np.cos(x) plt.plot(x,y,':') # y1 = np.cos(x-np.pi)/2 plt.plot(x-3*np.pi,y/2,color='b') plt.plot(x+3*np.pi,y/2,color='b') plt.xticks([-3*np.pi,0,3*np.pi],['$-\omega_0$','0','$-omega_0$']) plt.yticks([1],['$X(\omega)$']) plt.show()
# 矩形脉冲调制余弦载波 # 矩形脉冲 # x = np.arange(-1.5,1.5,0.1) # y = [0 for x in x if x <= -0.5] # y.extend([1 for x in x if x>-0.5 and x<=0.5]) # y.extend([0 for x in x if x>0.5]) # plt.plot(x,y) plt.subplot(3,2,1) x = [-1.5,-0.5,0.5,1.5] y = [0,1,0,0] plt.plot(x,y,drawstyle='steps-post') # cos(2\pi*5t),5Hz plt.subplot(3,2,3) x = np.arange(-1.5,1.6,0.1) y = np.cos(2*np.pi*5*x) plt.plot(x,y) # time zone modulation plt.subplot(3,2,5) y = [0 for x in x if x <= -0.4] y.extend([ np.cos(2*np.pi*5*x) for x in x if x>=-0.5 and x<=0.6]) y.extend([0 for x in x if x>=0.5]) x = np.sort(np.append(x,[0.5,-0.5])) plt.plot(x,y) plt.plot() # 矩形脉冲 Spectrum plt.subplot(3,2,2) f = np.arange(-4,4,0.1) y = np.sinc(f) plt.plot(f,y) # cos wave spectrum plt.subplot(3,2,4) f = [-5,5] y = [0.5,0.5] plt.stem(f,y) # modulation Spectrum plt.subplot(3,2,6) f = np.arange(-10,10,0.1) X = 0.5*np.sinc(f-5)+0.5*np.sinc(f+5) plt.plot(f,X) plt.tight_layout() plt.show()
无论信号经过多少处理,最终都会被转换成一连串脉冲(如矩形脉冲),再调制到载波发射出去
正脉冲与负脉冲的幅度谱和相位谱
# 正脉冲与负脉冲的幅度谱和相位谱
f = np.arange(-4,4,0.1)
plt.subplot(3,2,1)
X = abs(np.sinc(f))
plt.plot(f,X)
plt.title('postive pulse magnitude')
plt.subplot(3,2,3)
f = np.arange(-4,5,1)
P = [np.pi,0,np.pi,0,0,-np.pi,0,-np.pi,0]
plt.plot(f,P,drawstyle='steps-post')
plt.title('postive pulse phase')
f = np.arange(-4,4,0.1)
plt.subplot(3,2,2)
X = abs(-np.sinc(f))
plt.plot(f,X)
plt.title('negative pulse magnitude')
plt.subplot(3,2,4)
f = np.arange(-4,5,1)
P = [0,np.pi,0,np.pi,-np.pi,0,-np.pi,0,-np.pi]
plt.plot(f,P,drawstyle='steps-post')
plt.title('negative pulse phase')
plt.subplot(3,2,5)
x = np.arange(-1.5,2,0.5)
y=[0,0,0,1,1,0,0]
plt.plot(x,y,drawstyle='steps-pre')
plt.subplot(3,2,6)
y=[-1*t for t in y]
plt.plot(x,y,drawstyle='steps-pre')
plt.tight_layout()
plt.show()

# 连载84:采用对数坐标的矩形脉冲频谱
plt.subplot(2,1,1)
x = np.arange(-1.5,2,0.5)
y=[0,0,0,1,1,0,0]
plt.plot(x,y,drawstyle='steps-pre')
plt.subplot(2,1,2)
f=np.arange(-4,4.1,0.1)
X=abs(np.sinc(f))
plt.semilogy(f,X)
# plt.set_yscale('log')
plt.ylim([1.1*10**-6,1.1])
# plt.yticks([1.1,1.1*10**-2,1.1*10**-4,1.1*10**-6],['0','-20','-40','-60'])
# plt.ylabel('Aplitude(dB)')

BPSK调制解调频谱
# BPSK调制频谱
# input signal
plt.subplot(3,1,1)
t = np.arange(0,9,1)
d = [0,1,1,0,1,1,0,0,0]
plt.plot(t,d,drawstyle='steps-post')
plt.ylim([-0.5,1.5])
plt.annotate('0',xy=(0.5,1.2))
plt.text(1.5,1.2,'1',fontdict={'size':'8'})
# plt.annotate(['1','0'],xy=[(2.5,1.2),(3.5,1.2)]) #无法同时进行标注
# 基带调制信号(映射+基带调制)
plt.subplot(3,1,2)
t = np.arange(0,9,1)
d = [1,-1,-1,1,-1,-1,1,1,1]
plt.plot(t,d,drawstyle='steps-post')
plt.ylim([-1.5,1.8])
plt.annotate('1',xy=(0.5,1.2))
plt.annotate('-1',xy=(1.5,1.2))
# 频带调制信号(5Hz Cosine Wave)
plt.subplot(3,1,3)
t = np.arange(0,8.1,0.01)
y = [np.cos(2*np.pi*5*t) for t in t if t<1.1]
y.extend([np.cos(2*np.pi*5*t+np.pi) for t in t if 1.1<=t<3.1])
y.extend([np.cos(2*np.pi*5*t) for t in t if 3.1<=t<4.1])
y.extend([np.cos(2*np.pi*5*t+np.pi) for t in t if 4.1<=t<6.1])
y.extend([np.cos(2*np.pi*5*t) for t in t if 6.1<=t<8.1])
plt.plot(t,y)
plt.ylim([-1.8,1.8])
plt.annotate('0',xy=(0.5,1.2))
plt.annotate('$\pi$',xy=(1.5,1.2))
plt.tight_layout()

# 连载91 BPSK解调频域分析
# 时域采用cosine wave调制,便采用cosine wave解调,频域处理直观来看将频谱搬回原点便可采用低通滤波解调,时域处理直观来看在一个码元周期积分便可
# BPSK调制频谱
imgnum = 6
plt.figure(figsize=(5,10))
# input signal
plt.subplot(imgnum,1,1)
t = np.arange(0,9,1)
d = [0,1,1,0,1,1,0,0,0]
plt.plot(t,d,drawstyle='steps-post')
plt.ylim([-0.5,1.5])
plt.annotate('0',xy=(0.5,1.2))
plt.text(1.5,1.2,'1',fontdict={'size':'8'})
# plt.annotate(['1','0'],xy=[(2.5,1.2),(3.5,1.2)]) #无法同时进行标注
plt.title('input')
# 基带调制信号(映射+基带调制)
plt.subplot(imgnum,1,2)
t = np.arange(0,9,1)
d = [1,-1,-1,1,-1,-1,1,1,1]
plt.plot(t,d,drawstyle='steps-post')
plt.ylim([-1.5,1.8])
plt.annotate('1',xy=(0.5,1.2))
plt.annotate('-1',xy=(1.5,1.2))
plt.title('BPSK Base Band Modulation')
# 频带调制信号(5Hz Cosine Wave)
plt.subplot(imgnum,1,3)
t = np.arange(0,8.1,0.01)
y = [np.cos(2*np.pi*5*t) for t in t if t<1.1]
y.extend([np.cos(2*np.pi*5*t+np.pi) for t in t if 1.1<=t<3.1])
y.extend([np.cos(2*np.pi*5*t) for t in t if 3.1<=t<4.1])
y.extend([np.cos(2*np.pi*5*t+np.pi) for t in t if 4.1<=t<6.1])
y.extend([np.cos(2*np.pi*5*t) for t in t if 6.1<=t<8.1])
plt.plot(t,y)
plt.ylim([-1.8,1.8])
plt.annotate('0',xy=(0.5,1.2))
plt.annotate('$\pi$',xy=(1.5,1.2))
plt.title('BPSK Frequency Band Modulation')
# 频带解调信号,乘上cos(2*np.pi*5*t)
plt.subplot(imgnum,1,4)
t = np.arange(0,8.1,0.01)
y = y*np.cos(2*np.pi*5*t)
plt.plot(t,y)
plt.ylim([-1.8,1.8])
plt.title('BPSK Frequency Band Demodulation')
# 积分
plt.subplot(imgnum,1,5)
y = [1,-1,-1,1,-1,-1,1,1,1]
plt.plot(y,drawstyle='steps-post')
plt.axhline(color='black')
plt.title('Intergration')
# 会付出输入信号
plt.subplot(imgnum,1,6)
x = np.arange(1,9,1)
y = [1,-1,-1,1,-1,-1,1,1]
plt.stem(x,y,use_line_collection=True)
plt.xlim(0,8.2)
plt.ylim(-1.5,1.5)
plt.axhline(color='b')
plt.title('Recover Bits')
plt.tight_layout()

连载93 BPSK解调
法1(时域):接收信号乘上\(\cos\omega_0t\)再对码元周期内进行积分便可会付出传输信号x(t)
法2 (频域) :接收信号乘上\(\cos\omega_0t\)再进行傅里叶变换(进入频域)得到频谱后进行低通滤波滤除高频分类后再进行傅里叶逆变换(回到时域)恢复出传输信号x(t)
DSP使得快速傅里叶变得应用广泛,使得频域处理简单
连载86 正负矩形脉冲调制正余弦载波
# 连载86 三维频谱:包含幅度和相位信息
f = np.arange(1,9.01,0.01)
x = 0.5*np.sinc(f-5)
fig = plt.figure()
# ax = fig.gca(projection='3d')
ax = fig.add_subplot(1,2,1,projection='3d')
ax.plot(f,x,0*x,label='positive side',color='r')
f = np.arange(-9.01,-1,0.01)
x = 0.5*np.sinc(f+5)
ax.plot(f,x,0*x,label='negative side',color='r')
# ax.legend()
ax.set_title('正矩形脉冲调制余弦载波', fontproperties='stsong')
# fig = plt.figure()
ax2 = fig.add_subplot(1,2,2,projection='3d')
f2 = np.arange(-9.01,-1,0.01)
x2 = -0.5*np.sinc(f2+5)
ax2.plot(f2,x2,0*x2,label='positive side',color='r')
f2 = np.arange(1,9.01,0.01)
x2 = -0.5*np.sinc(f2-5)
ax2.plot(f2,x2,0*x2,label='negative side',color='r')
# ax2.set_title('$\\tau$=1 negative Square wave to modulate the cosine wave spectrum')
ax2.set_title('负矩形脉冲调制余弦载波', fontproperties='stsong')
plt.tight_layout()

# 连载88
f = np.arange(1,9.01,0.01)
x = 0.5*np.sinc(f-5)
fig = plt.figure()
# ax = fig.gca(projection='3d')
ax = fig.add_subplot(1,2,1,projection='3d')
ax.plot(f,x,0*x,label='positive side',color='r')
f = np.arange(-9.01,-1,0.01)
x = 0.5*np.sinc(f+5)
ax.plot(f,x,0*x,label='negative side',color='r')
# ax.legend()
ax.set_title('正矩形脉冲调制余弦载波', fontproperties='stsong')
ax2 = fig.add_subplot(1,2,2,projection='3d')
f2 = np.arange(-9.01,-1,0.01)
y = 0.5*np.sinc(f2+5)
ax2.plot(0*f2,f2,y,label='positive side',color='r')
f2 = np.arange(1.01,9,01.01)
y = -0.5*np.sinc(f2-5)
ax2.plot(0*f2,f2,y,label='negative side',color='r')
# ax.legend()
ax2.set_title('正矩形脉冲调制正弦载波', fontproperties='stsong')
ax2.set_xlabel('x')
ax2.set_ylabel('f')
ax2.set_zlabel('y')
ax2.view_init(30,20)
plt.tight_layout()
plt.show()

QPSK调制解调
# 连载94: QPSK 时域 调制解调
imgnum = 6
a = 1/np.sqrt(2)
plt.figure(figsize=(5,10))
# input signal
plt.subplot(imgnum,1,1)
# t = np.arange(0,8.5,0.5)
# d = [0,1,1,0,1,1,0,0,0,1,1,0,1,1,0,0,0]
t = np.arange(0,4.5,0.5)
d = [0,1,1,0,1,1,0,0,0]
plt.plot(t,d,drawstyle='steps-post')
plt.ylim([-0.5,1.5])
# plt.annotate('0',xy=(0.5,1.2))
# plt.text(1.5,1.2,'1',fontdict={'size':'8'})
plt.title('QPSK input')
# I signal
plt.subplot(imgnum,1,2)
x = np.arange(0,5,1)
d = [-a,a,-a,a,a]
plt.plot(x,d,drawstyle='steps-post')
plt.ylim([-1.5,1.5])
plt.annotate('$-\\sqrt{2}$',xy=(0.5,1))
plt.annotate('$\\sqrt{2}$',xy=(1.5,1))
plt.title('Q signal')
# Q signal
plt.subplot(imgnum,1,3)
x = np.arange(0,5,1)
d = [a,-a,-a,a,a]
plt.plot(x,d,drawstyle='steps-post')
plt.ylim([-1.5,1.5])
plt.annotate('$\\sqrt{2}$',xy=(0.5,1))
plt.annotate('$-\\sqrt{2}$',xy=(1.5,1))
plt.title('Q signal')
# 频带调制信号
plt.subplot(imgnum,1,4)
t = np.arange(0,4.1,0.01)
y = [np.cos(2*np.pi*5*t+3/4*np.pi) for t in t if t<1.1]
y.extend([np.cos(2*np.pi*5*t+7/4*np.pi) for t in t if 1.1<=t<2.1])
y.extend([np.cos(2*np.pi*5*t+5/4*np.pi) for t in t if 2.1<=t<3.1])
y.extend([np.cos(2*np.pi*5*t+1/4*np.pi) for t in t if 3.1<=t<4.1])
# t = np.arange(0,8.2,0.1)
# y = y*2
# y.extend([np.cos(2*np.pi*5*t) for t in t if 6.1<=t<8.1])
plt.plot(t,y)
plt.ylim([-1.8,1.8])
# plt.annotate('0',xy=(0.5,1.2))
# plt.annotate('$\pi$',xy=(1.5,1.2))
plt.title('QPSK Frequency Band Modulation')
# I Signal
plt.subplot(imgnum,1,5)
yI = y*np.cos(2*np.pi*5*t)
plt.plot(t,yI)
# Q Signal
plt.subplot(imgnum,1,6)
yQ = y*-np.sin(2*np.pi*5*t)
plt.plot(t,yQ)
plt.tight_layout()

[连载95]是QPSK频域解调3维形式
[连载238]加入升余弦滚降滤波器后的QPSK波形
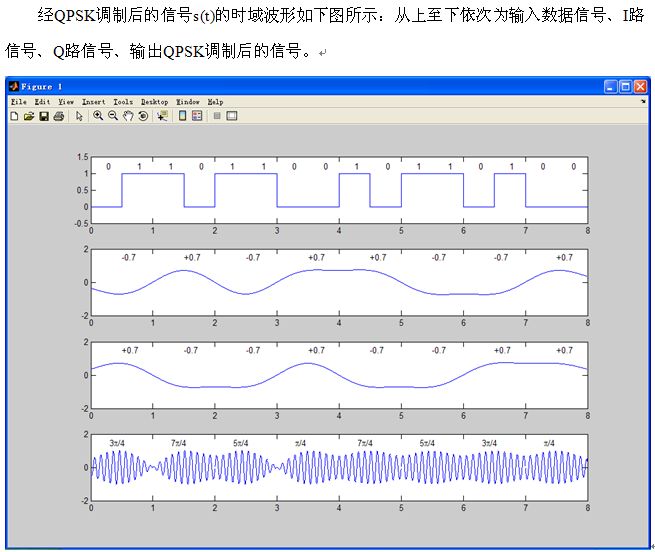
当前一码元与后一码元的相位差相差pi时,信号包络会穿过零点
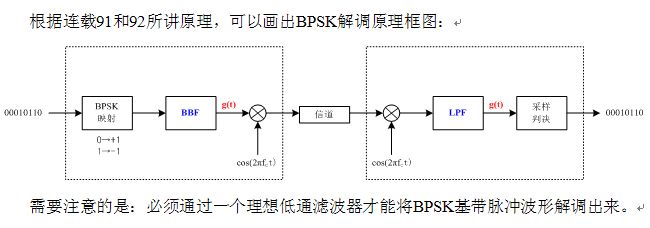
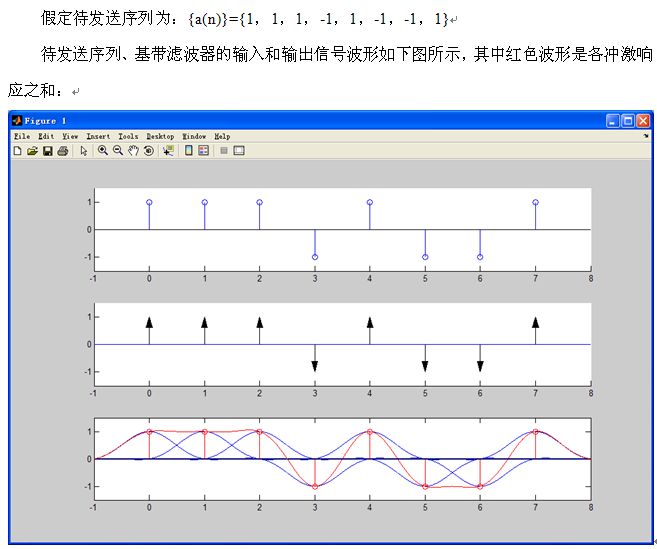
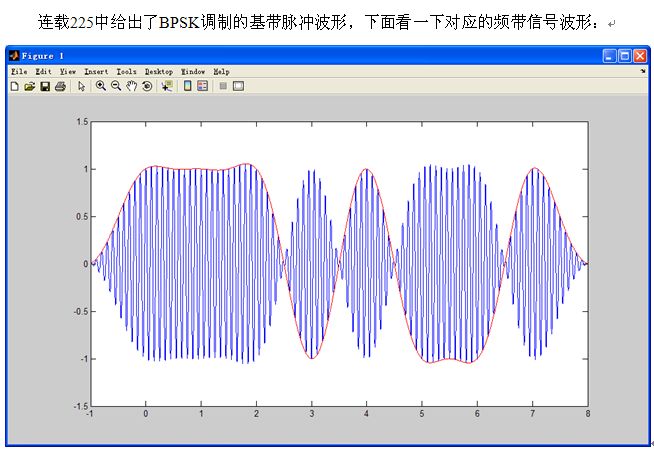
连载226 BPSK完整调制解调
本博客由博主原创,链接:https://www.cnblogs.com/WindyZ/




 浙公网安备 33010602011771号
浙公网安备 33010602011771号