noip模拟67
考试过程:读一遍题觉得比较有难度,就从看起来比较可做的T1开始。
我以为这是个树形DP,但是想了想没什么思路,只想到一个复杂度可以达到\(o(n^2)\)的做法,但是我不会\(o(n)\)对子树信息进行合并,就放了。
后面几个题同样是没什么思路,就打了几个暴搜。
但是T3,T4我忘了取模,导致我没有拿到那一部分暴力分。
总结:考试中的暴力分一定不能白丢,做完题之后可以再读一遍题面进行检查。
T1 数据恢复
思路:先从菊花图说起,假如我们不考虑父节点的影响,想使得总价值最大,那么我们可以对于每个物品按照\(a/b\)排序后从小到大选。证明:假设\(j<i\)要让\(i\)在\(j\)后面被选的条件是\(b_j\times a_i >a_j\times b_i\),化简一下即可。

这里说一下合并操作,我们可以给每个点一个\(id\)和\(pos\),这个\(pos\)是不断自加的,在将儿子合并到父亲的过程中将新的点的编号设为pos,那么当前点在操作完后就被\(pop\)了,我们可以不管。对于这个点的\(fa\),我们将他的\(no[pos]=1\),以后再遇到直接\(continue\)即可。
代码如下:
AC_code
#include<bits/stdc++.h>
#define int long long
#define re register int
#define ii inline int
#define iv inline void
#define f() cout<<"fuck"<<endl
#define head heeead
#define next neet
using namespace std;
const int N=3e5+10;
int n,ans,jb,timi;
int fa[N*30],be[N*30];
bool vis[N*30],no[N*30];
struct node
{
int a,b,id,pos;
friend bool operator < (node x,node y) {return x.a*y.b>x.b*y.a;}
}cun[N*30];
priority_queue<node> q;
ii read()
{
int x=0;char ch=getchar();bool f=1;
while(ch<'0' or ch>'9')
{
if(ch=='-') f=0;
ch=getchar();
}
while(ch>='0' and ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f?x:(-x);
}
ii gett(int x) {return x==be[x]?x:be[x]=gett(be[x]);}
signed main()
{
freopen("data.in","r",stdin),freopen("data.out","w",stdout);
n=read();
for(re i=2;i<=n;i++)
fa[i]=read();
for(re i=1;i<=n;i++) cun[i]=(node){read(),read(),i,i};
for(re i=2;i<=n;i++) q.push(cun[i]);
for(re i=1;i<=n;i++) be[i]=i;
int cnt=n;
vis[1]=1;
timi=n;
jb=cun[1].b;
while(q.size())
{
++timi;
int y=q.top().pos,x=q.top().id;
if(no[y]) {q.pop();continue;}
int fx=gett(fa[x]);
if(vis[fx])
{
vis[x]=1,--cnt,ans+=jb*q.top().a,jb+=q.top().b;
q.pop();
}
else
{
be[x]=fx;
ans+=cun[fx].b*q.top().a;
no[cun[fx].pos]=1;
cun[fx]=(node){cun[fx].a+q.top().a,cun[fx].b+q.top().b,cun[fx].id,timi};
q.pop();
q.push(cun[fx]);
--cnt;
}
}
printf("%lld\n",ans);
return 0;
}
T2 下落的小球
前置芝士 :可重集排列
若\(\sum^{n}_{i=1}x_i==K\),\(x_i\)是每种元素的\(size\),那么对于这些数组成的序列的排列方案数为\(\frac{K!}{\prod^{n}_{i=1}(x_i)!}\)
思路:因为\(\sum^{n}_{i=1}a_i==n\),所以若使得所有球都被取出,那么就要让每个点跑满。
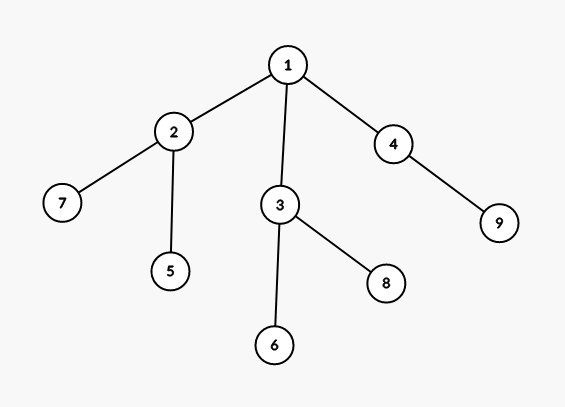
对于这张图,我们以\(1\)为跟,那么我们可以得到以\(2,3,4\)为跟的子树的\(size\)和\(a_i\)之和,为了满足题意,每个子树需要上面补的球的数量为\(\sum a_i-size\),所以从上面往下掉球的方案数为可重集排列的方案数。
接下来考虑子树之间的方案,因为子树内部掉球顺序可变,所以这些\(size\)还要做一个可重集排列,最后再将这些方案相乘即可。
代码如下:
AC_code
#include<bits/stdc++.h>
#define int long long
#define re register int
#define ii inline int
#define iv inline void
#define f() cout<<"fuck"<<endl
#define head heeead
#define next neet
using namespace std;
const int N=1e6+10;
const int mo=1e9+7;
int n,tot,ans=1;
int fa[N],a[N],size[N],sum[N],v[N];
int to[N<<1],next[N<<1],head[N];
int jc[N],inv[N],pos[N];
ii read()
{
int x=0;char ch=getchar();bool f=1;
while(ch<'0' or ch>'9')
{
if(ch=='-') f=0;
ch=getchar();
}
while(ch>='0' and ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f?x:(-x);
}
iv add(int x,int y)
{
to[++tot]=y;
next[tot]=head[x];
head[x]=tot;
}
ii ksm(int d,int z)
{
int out=1;
while(z)
{
if(z&1) out=out*d%mo;
z>>=1;
d=d*d%mo;
}
return out;
}
iv dfs(int st,int f)
{
size[st]=1;
sum[st]=a[st];
int dn1=1,dn2=1;
for(re i=head[st];i;i=next[i])
{
int p=to[i];
if(p==f) continue;
dfs(p,st);
size[st]+=size[p];dn1=dn1*jc[size[p]]%mo;
sum[st]+=sum[p];dn2=dn2*jc[(sum[p]-size[p])]%mo;
}
dn1=ksm(dn1,mo-2),dn2=ksm(dn2,mo-2);
if(head[st]) ans=ans*jc[size[st]-1]%mo*dn1%mo*jc[sum[st]-size[st]+1]%mo*dn2%mo;
}
signed main()
{
freopen("ball.in","r",stdin),freopen("ball.out","w",stdout);
n=read();
jc[0]=1;
for(re i=1;i<N;i++) jc[i]=jc[i-1]*i%mo;
inv[N-1]=ksm(jc[N-1],mo-2)%mo;
for(re i=N-2;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mo;
for(re i=2;i<=n;i++) fa[i]=read(),add(fa[i],i);
for(re i=1;i<=n;i++) a[i]=read();
dfs(1,0);
printf("%lld\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号