noip模拟测试12
老样子,还是先写一下自己的考试经过,首先看题面,觉得开题顺序1 2 3,同时,注意到T2为一个类似于退式子的题,吸取v上次的教训,给他留出足够时间。
首先是 T1,我又想到了线段树,但是没有想到正解,但是我想到一个 n^n/2 的分组算法,但是比较麻烦,没有分出来,就打了个暴力,一共用时一小时左右
第二题,一看就是个跟平时数学文化课作业难度差不多的一个概率题,但是我当时看错了 n,m 的输入顺序,导致我的结果和样例一个都对不上,用了差不多一个小时才发现自己把 m,n 看反了
发现之后就很好说了,五分钟左右就推出了式子,但是这个式子要求取模并约分,我当时就怀疑直接取模计算的正确性,但是没什么好的想法,就直接打了
T3,我当时想到了贪心,但是我的贪心思路没有正确性,正解的贪心思路真是妙,接下来我对每道题进行详细解析:
T1:这道题思路来自: https://www.cnblogs.com/hzoi-fengwu
这道题类似与昨天的T3,同样的,我们可以利用单调队列求出每个 a[i] ,当作最大值的左右区间,区间没有交集,并利用启发式合并的思想,暴力枚举小的区间,理智处理较大区间,
这样就可以省去枚举左右端点。利用入阵曲的思路,若 a ,b,在 %p 意义下同余,(设 a>b ) 则 (a-b) 可以被 p 整除。
那么我们就可以利用一个vector数组,第一维存模,第二维存元素的位置,以上就是预处理的过程
接下来就是一个非常秒的计算,我们以左区间小于右区间为例,我们从 [L,p],枚举每一个sum[i-1],因为满足条件的右端点 x 必定满足 ,sum[x]==((sum[i-1]+a[p])%k),
我们设 X=((sum[i-1]+a[p])%k),那么我们通过计算Y=lower_bound(v[X].begin(),v[X].end(),p)-v[X].begin(),和Z=upper_bound(v[X].begin(),v[X].end(),R)-v[X].begin();做差即可求出满足条件的右端点个数
最后 ans+=Z-Y即可
注意,当左区间大于右区间时,因为我们要查询 Y=lower_bound(v[X].begin(),v[X].end(),L-1)-v[X].begin(),当 L==1时,会查到0,所以我们对于 v[0].push_back(0),意思就是前0位的前缀和为 0,%p后余数也为零
代码如下:
1 #include<bits/stdc++.h>
2 #define int long long
3 #define re register int
4 #define iv inline void
5 #define ii inline int
6 #define lc rt<<1
7 #define rc rt<<1|1
8 #define mid ((l+r)>>1)
9 using namespace std;
10 const int N=5e6+10;
11 int n,k;
12 int a[N],l[N],r[N],sum[N],ans;
13 stack <pair<int,int> > s;
14 vector <int> v[N];
15 ii read()
16 {
17 int x=0,f=1;
18 char ch=getchar();
19 while(ch<'0'||ch>'9')
20 {
21 if(ch=='-')
22 f=0;
23 ch=getchar();
24 }
25 while(ch>='0'&&ch<='9')
26 {
27 x=(x<<1)+(x<<3)+(ch^48);
28 ch=getchar();
29 }
30 return (f)?x:(-x);
31 }
32 void in()
33 {
34 for(re i=1;i<=n;i++)
35 {
36 while(!s.empty()&&a[i]>=s.top().first)
37 {
38 r[s.top().second]=i-1;
39 s.pop();
40 }
41 s.push(make_pair(a[i],i));
42 }
43 int L=s.top().second;
44 while(!s.empty())
45 {
46 r[s.top().second]=L;
47 s.pop();
48 }
49 for(re i=n;i;i--)
50 {
51 while(!s.empty()&&a[i]>s.top().first)
52 {
53 l[s.top().second]=i+1;
54 s.pop();
55 }
56 s.push(make_pair(a[i],i));
57 }
58 int R=s.top().second;
59 while(!s.empty())
60 {
61 l[s.top().second]=R;
62 s.pop();
63 }
64 }
65 iv workk(int p,int L,int R)
66 {
67 if(p-L<R-p)
68 {
69 int X,Y,Z;
70 for(re i=L;i<=p;i++)
71 {
72 X=(sum[i-1]+a[p])%k;
73 Y=lower_bound(v[X].begin(),v[X].end(),p)-v[X].begin();
74 Z=upper_bound(v[X].begin(),v[X].end(),R)-v[X].begin();
75 ans+=max(0*1ll,Z-Y);
76 }
77 }
78 else
79 {
80 int X,Y,Z;
81 for(re i=p;i<=R;i++)
82 {
83 X=(sum[i]-a[p]%k+k)%k;
84 Y=lower_bound(v[X].begin(),v[X].end(),L-1)-v[X].begin();
85 Z=upper_bound(v[X].begin(),v[X].end(),p-1)-v[X].begin();
86 ans+=max(0ll,Z-Y);
87 }
88 }
89 }
90 #undef int
91 int main()
92 {
93 #define int long long
94 n=read();
95 k=read();
96 for(re i=1;i<=n;i++)
97 a[i]=read();
98 in();
99 for(re i=0;i<k;i++)
100 v[i].push_back(0);
101 for(re i=1;i<=n;i++)
102 sum[i]=(sum[i-1]+a[i])%k;
103 for(re i=1;i<=n;i++)
104 v[sum[i]%k].push_back(i);
105 for(re i=1;i<=n;i++)
106 workk(i,l[i],r[i]);
107 ans-=n;
108 printf("%lld\n",ans-());
109 return 0;
110 }
T2
这道题式子很好推,就是 ( ( C^m,(2^n) ) *m! )/2^(n*m), == ( ((2^n)!) / (((2^n)-m)!) )/(2^(n*m));
上面的部分就是 (2^n) *((2^n) -1) *((2^n)-2)* ..... *((2^n)-m+1) , 也就是m 个连续的数相乘
那么显然,当 m>mo 时,分子就是 0
接下来我们考虑约分,这道题麻烦的地方就在于不能用 gcd ,因为模了一个数后结果会不对
有这样一个结论,

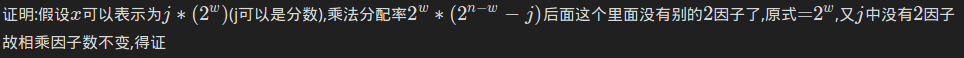
那么分子就转化成求 (m-1)! 中的2的因子数
可以这样求:
for(re i=2;i<m;i<<=1) ans+=(m-1)/i;

最后,我们利用逆元的性质求出答案即可
代码如下:
#include<bits/stdc++.h>
#define int long long
#define re register int
#define iv inline void
#define ii inline int
#define lc rt<<1
#define rc rt<<1|1
#define mid ((l+r)>>1)
using namespace std;
int m,n,sum,U,D;
int mo=1e6+3;
inline long long read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
f=0;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return (f)?x:(-x);
}
ii ksm(int d,int z)
{
int out=1;
while(z)
{
if(z&1)
out=out*d%mo;
z>>=1;
d=d*d%mo;
}
return out%mo;
}
#undef int
int main()
{
#define int long long
n=read();
m=read();
if(log2(m)>n)
{
printf("1 1\n");
return 0;
}
U=1,D=1;
int base=ksm(2,n),ans=0,inv;
D=ksm(base,m-1);
for(re i=2;i<m;i<<=1)
ans+=(m-1)/i;
inv=ksm(ksm(2,ans),mo-2);
if(m<=mo)
for(re i=1;i<m;i++)
U=U*(base-i)%mo;
else
U=0;
U=(U%mo*inv%mo+mo)%mo;
D=(D%mo*inv%mo+mo)%mo;
printf("%lld %lld\n",((D-U+mo)%mo+mo)%mo,(D+mo)%mo);
return 0;
}
T3
一道思路非常妙的贪心题

那么我们就开两个二元组,up,down,按照上述思路操作即可
具体来说,我们先正着扫一遍,先不考虑是否当前位置有数,继承up 和 down
up两位一进,down五位一进
考虑已经填的,先考虑上界,若a[i]>up,比上界大肯定不合法,若a[i]=up,不管,若a[i]<up,则将up调整到a[i]次数变为2,下界类似,若a[i]<down,比下界小不合法,若a[i]>down,将down调整到a[i],统计答案时反着扫
最后输出的时候记得右端点特判
代码如下:
1 #include<bits/stdc++.h>
2 #define int long long
3 #define re register int
4 #define iv inline void
5 #define ii inline int
6 #define lc rt<<1
7 #define rc rt<<1|1
8 #define mid ((l+r)>>1)
9 using namespace std;
10 const int N=2e5+10;
11 int n,ans=-1,maxn;
12 int a[N],vis[N],v[N],cun[N];
13 pair<int,int> up[N],down[N];
14 ii read()
15 {
16 int x=0,f=1;
17 char ch=getchar();
18 while(ch<'0'||ch>'9')
19 {
20 if(ch=='-')
21 f=0;
22 ch=getchar();
23 }
24 while(ch>='0'&&ch<='9')
25 {
26 x=(x<<1)+(x<<3)+(ch^48);
27 ch=getchar();
28 }
29 return (f)?x:(-x);
30 }
31 #undef int
32 int main()
33 {
34 #define int long long
35 n=read();
36 for(re i=1;i<=n;i++)
37 a[i]=read(),vis[a[i]]++;
38 up[1].first=up[1].second=down[1].first=down[1].second=1;
39 bool noo=0;
40 for(re i=2;i<=n;i++)
41 {
42 if(up[i-1].second==2)
43 {
44 up[i].first=up[i-1].first+1;
45 up[i].second=1;
46 }
47 else
48 {
49 up[i].first=up[i-1].first;
50 up[i].second=up[i-1].second+1;
51 }
52 if(down[i-1].second==5)
53 {
54 down[i].first=down[i-1].first+1;
55 down[i].second=1;
56 }
57 else
58 {
59 down[i].first=down[i-1].first;
60 down[i].second=down[i-1].second+1;
61 }
62 if(a[i])
63 {
64 if(a[i]>up[i].first)
65 {
66 noo=1;
67 break;
68 }
69 if(a[i]<down[i].first)
70 {
71 noo=1;
72 break;
73 }
74 if(a[i]<up[i].first)
75 {
76 up[i].first=a[i];
77 up[i].second=2;
78 }
79 if(a[i]>down[i].first)
80 {
81 down[i].first=a[i];
82 down[i].second=1;
83 }
84 }
85 }
86 if(noo)
87 {
88 printf("-1\n");
89 return 0;
90 }
91 if(a[n])
92 cun[n]=a[n];
93 else
94 {
95 cun[n]=up[n-1].first;
96 ++vis[cun[n]];
97 }
98 for(re i=n-1;i;i--)
99 {
100 if(a[i])
101 cun[i]=a[i];
102 else
103 {
104 int tmp=min(up[i].first,cun[i+1]);
105 while(vis[tmp]==5)
106 --tmp;
107 cun[i]=tmp;
108 ++vis[cun[i]];
109 }
110 }
111 printf("%lld\n",cun[n]);
112 for(re i=1;i<=n;i++)
113 printf("%lld ",cun[i]);
114 return 0;
115 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号