遥远的国度 (树链剖分换根),洛谷P3979
析:显然,若没有换根操作,则为树链剖分板子题,但是这道题我们考虑换根操作
考虑这样一个性质:在一棵树上,两点的距离路径是唯一的!!
也就是说,我们在修改路径上的点权时,不必考虑根在哪里,直接利用模板修改即可
麻烦的地方在于查询操作,我分了三种情况来讨论:(设 root 为当前的根,id 为当前要查询的编号)
1.若 deep[id]>=deep[root] ,则跟对他没有影响,直接查询即可
2.若 deep[id]<deep[root] ,刚开始我是求出两点的 LCA ,然后查询 (1,num[lca]) 和 (num[root]+size[root],n)
但是,这样会出现一些问题,比如这张图:
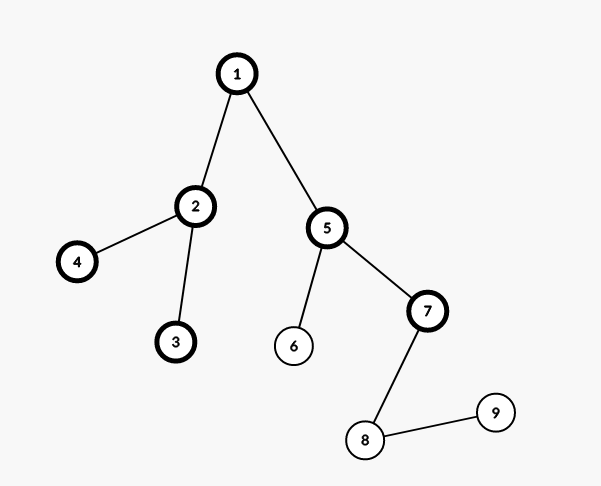
当 root=7,id==5 时,我们这样查询就会漏掉 6
那么我们能不能这样写呢 ? 查询(1,num[root]-1) 和(num[root]+size[root],n);
显然也是不能的(虽然这数据比较水,这样写会多得几分),如下图:
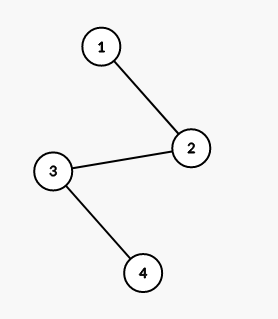
当 root==4 ,id==2 时,这样查询就会多出来一个点 3
这...........可如何是好?
其实,应该有大佬已经发现了,无论是什么情况,我们查询的边界始终是 (1,num[son[lca]]-1)和 (num[son[lca]+size[son[lca]]] , n)
所以,我们只需查询 root 和 id 的 lca 的重儿子即可(保证在同一条链上)
代码如下:
#include<bits/stdc++.h>
#define re register int
#define next nett
#define lc rt<<1
#define rc rt<<1|1
#define mid ((l+r)>>1)
#define ii inline int
#define iv inline void
using namespace std;
const int N=1e6+10;
struct CUN
{
int minn,lazy;
}use[N<<4];
int n,m,root,timi,tot,lcas;
int to[N<<1],next[N<<1],head[N],num[N],top[N],son[N],deep[N],fa[N],size[N],chu[N],zh[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
f=0;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return (f)?x:(-x);
}
ii add(int x,int y)
{
to[++tot]=y;
next[tot]=head[x];
head[x]=tot;
}
iv dfs1(int st,int f)
{
size[st]=1;
fa[st]=f;
deep[st]=deep[f]+1;
for(re i=head[st];i;i=next[i])
{
int p=to[i];
if(p==f)
continue;
dfs1(p,st);
size[st]+=size[p];
son[st]=(size[son[st]]>size[p])?son[st]:p;
}
}
iv dfs2(int st,int t)
{
top[st]=t;
num[st]=++timi;
zh[timi]=chu[st];
if(!son[st])
return;
dfs2(son[st],t);
for(re i=head[st];i;i=next[i])
{
int p=to[i];
if(p==fa[st]||p==son[st])
continue;
dfs2(p,p);
}
}
iv pp(int rt)
{
use[rt].minn=min(use[lc].minn,use[rc].minn);
}
iv build(int rt,int l,int r)
{
if(l==r)
{
use[rt].minn=zh[l];
return;
}
build(lc,l,mid);
build(rc,mid+1,r);
pp(rt);
}
ii gett(int x,int y)
{
int fx=top[x],fy=top[y];
while(fx!=fy)
{
if(deep[fx]<deep[y])
swap(x,y),swap(fx,fy);
if(fa[fx]==y)
return fx;
x=fa[fx];
fx=top[x];
}
if(deep[x]>deep[y])
swap(x,y);
return son[x];
}
iv pd(int rt,int l,int r)
{
if(use[rt].lazy)
{
use[lc].minn=use[rt].lazy;
use[rc].minn=use[rt].lazy;
use[lc].lazy=use[rc].lazy=use[rt].lazy;
use[rt].lazy=0;
}
}
iv change(int rt,int l,int r,int L,int R,int z)
{
if(R<l||r<L||L>R) return ;
if(L<=l&&r<=R)
{
use[rt].minn=z;
use[rt].lazy=z;
return;
}
pd(rt,l,r);
if(mid>=L)
change(lc,l,mid,L,R,z);
if(mid<R)
change(rc,mid+1,r,L,R,z);
pp(rt);
}
ii query(int rt,int l,int r,int L,int R)
{
if(R<l||r<L||L>R) return 999999999;
if(L<=l&&r<=R)
return use[rt].minn;
pd(rt,l,r);
if(mid>=R)
return query(lc,l,mid,L,R);
if(mid<L)
return query(rc,mid+1,r,L,R);
return min(query(lc,l,mid,L,R),query(rc,mid+1,r,L,R));
}
iv upd(int x,int y,int z)
{
int fx=top[x],fy=top[y];
while(fx!=fy)
{
if(deep[fx]<deep[fy])
swap(x,y),swap(fx,fy);
change(1,1,n,num[fx],num[x],z);
x=fa[fx];
fx=top[x];
}
if(deep[x]>deep[y])
swap(x,y);
change(1,1,n,num[x],num[y],z);
}
int main()
{
n=read();
m=read();
int a,b,c,d,lca;
for(re i=1;i<n;i++)
{
a=read();
b=read();
add(a,b);
add(b,a);
}
for(re i=1;i<=n;i++)
chu[i]=read();
root=1;
dfs1(root,root);
dfs2(root,root);
build(1,1,n);
root=read();
while(m--)
{
a=read();
if(a==1)
{
root=read();
continue;
}
if(a==2)
{
b=read();
c=read();
d=read();
upd(b,c,d);
}
if(a==3)
{
b=read();
if(b==root)
{
printf("%d\n",query(1,1,n,1,n));
continue;
}
lcas=gett(b,root);
if(deep[b]>=deep[root])
printf("%d\n",query(1,1,n,num[b],num[b]+size[b]-1));
else if(fa[lcas]==b)
printf("%d\n",min(query(1,1,n,1,num[lcas]-1),query(1,1,n,num[lcas]+size[lcas],n)));
else
printf("%d\n",query(1,1,n,num[b],num[b]+size[b]-1));
continue;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号