最短母串
E. 最短母串
内存限制:512 MiB 时间限制:1000 ms 标准输入输出
题目类型:传统 评测方式:文本比较
题目描述
原题来自:HNOI 2006
给定n个字符串 ,要求找到一个最短的字符串s ,使得这 n个字符串都是s的子串。
输入格式
第一行是一个正整数n,表示给定的字符串的个数;
以下的n行,每行有一个全由大写字母组成的字符串。
输出格式
只有一行,为找到的最短的字符串。
在保证最短的前提下,如果有多个字符串都满足要求,那么必须输出按字典序排列的第一个。
样例
样例输入
2
ABCD
BCDABC
样例输出
ABCDABC
析:这是道AC自动机好题,同时利用了状压的思想,我们将 flag 置为 (1<<(i-1)) ,那么当我们搜索到的状态 s==((1<<n)-1) 时,即为满足条件的最短母串 (状压??,没错,就是个比较不一样的状压题)
这道题的 bfs 相当妙,我们首先开两个队列,Q1, Q2 ,Q1用来存储当前的位置,Q2用来枚举状态,那么我们的边界条件就是 Q2.top()==(1<<n)-1;
下面我详细的说一下 bfs 的过程,首先,若以当前点为起点的 son[i] 没有被遍历过,那么我们首先将他的 vis 数组=1,然后将其 (包括其更新的状态 ) 放入队列,这里同时用到了两个数组,fa 用来记录每次连边的 father,这个在最后输出结果时有用,net 用来记录每次连边的字符,
(显然,我们如果直接存储一段字符串是很难处理的,那么我们就存储字符), my 表示当前的层数,在每一次搜寻结束后累加;
接下来是我们输出答案的过程,这里可能有些难理解,建议自己手模一下,首先,我们要理解 get_fail() 中的操作: if(!v)
use[u].son[i]=use[Fail].son[i];
这里的操作就是我们利用 bfs 计算的正确性所在,如果我们现在的节点没有这个儿子,那么他的儿子就是他的 Fail 指针的儿子,如图:
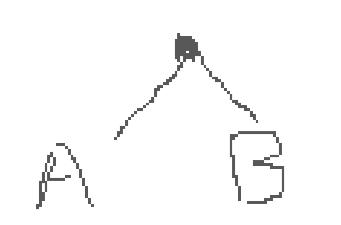
这样我们就可以在遍历到 A 的时候将 B 的状态加入队列;
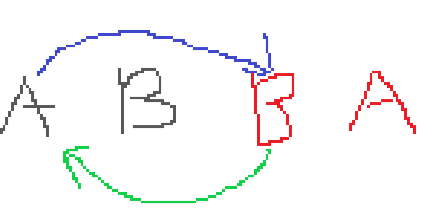
蓝色箭头表示 在遍历到 A 的时候将 B 加入了队列,并更新了状态
绿色箭头表示输出时回溯的过程
看一下输出的过程:
void pr(int x)
{
if(!x)
return;
pr(fa[x]);
putchar(net[x]+'A');
}
if(t==((1<<n)-1))
{
pr(my);
return;
}
但是我们注意到我们在存储的过程中:
if(!vis[use[now].son[i]][t|use[use[now].son[i]].flag]&&use[now].son[i]>1)
{
vis[use[now].son[i]][t|use[use[now].son[i]].flag]=1;
fa[++tot]=my;
net[tot]=i;
Q1.push(use[now].son[i]);
Q2.push(t|use[use[now].son[i]].flag);
}
这里为什么不用 tot,要用 my 呢?
首先我们要明确一个事情,每次我们将一个字符 Push 进队列的时候,都相当于从这个点向外连了一条边,但是,有些边可能是重复的,那么我们最终需要的答案就是当 t==(1<<n)-1 时,这是很显然当前的字符为最终答案的末尾,那么我们就要从当前这个点连边的 father
不停向上回溯,最终输出答案。最后再解释一下为什么从 my 开始回溯,因为我已知当前点为末尾,那么我当前的 my 一定与我的最后一条连我的边的编号相同!!,到这里应该解释的比较清楚了;
哦,最后还有一点,就是可能会有重复的单词,那我们在初始化的时候就要:
use[now].flag|=(1<<(pos-1));
这样无论如何我们都能将其加入计算
代码:
#include<bits/stdc++.h>
#define re register int
using namespace std;
const int N=700;
int n,num=1,ed,tot,cnt,my;
int fa[N*(1<<13)],net[N*(1<<13)];
char s[N];
bool vis[N*30][1<<14];
queue<int> q;
queue<int> Q1,Q2;
struct CUN
{
int fail,flag;
int son[30];
}use[N*30];
void insert(char ss[],int pos)
{
int now=1;
int l=strlen(ss);
for(re i=0;i<l;i++)
{
int p=ss[i]-'A';
if(!use[now].son[p])
use[now].son[p]=++num;
now=use[now].son[p];
}
use[now].flag|=(1<<(pos-1));
}
void get_fail()
{
for(re i=0;i<26;i++)
use[0].son[i]=1;
use[1].fail=0;
q.push(1);
while(!q.empty())
{
int u=q.front();
q.pop();
int Fail=use[u].fail;
for(re i=0;i<26;i++)
{
int v=use[u].son[i];
if(!v)
{
use[u].son[i]=use[Fail].son[i];
continue;
}
use[v].fail=use[Fail].son[i];
use[v].flag|=use[use[v].fail].flag;
q.push(v);
}
}
}
void pr(int x)
{
if(!x)
return;
pr(fa[x]);
putchar(net[x]+'A');
}
void bfs()
{
Q1.push(1); //位置
Q2.push(0); //状态
vis[1][0]=1;
for(re i=0;i<(1<<n);i++)
vis[0][i]=1;
while(!Q1.empty())
{
int now=Q1.front();
int t=Q2.front();
Q1.pop();
Q2.pop();
if(t==((1<<n)-1))
{
pr(my);
return;
}
for(re i=0;i<26;i++)
{
if(!vis[use[now].son[i]][t|use[use[now].son[i]].flag]&&use[now].son[i]>1)
{
vis[use[now].son[i]][t|use[use[now].son[i]].flag]=1;
fa[++tot]=my;
net[tot]=i;
Q1.push(use[now].son[i]);
Q2.push(t|use[use[now].son[i]].flag);
}
}
++my;
}
}
int main()
{
scanf("%d",&n);
for(re i=1;i<=n;i++)
{
scanf("%s",s);
insert(s,i);
}
get_fail();
bfs();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号