noip模拟测试7
A. 匹配
题目描述

一道比较水的模板题,理论上应该考场AC,但由于数组开小了,导致WA了一个测试点。。。(惨痛的教训)
这道题大概思路有两种,第一种就是用 hash ,o(n)的复杂度判断,我就是这样做的,第二种就是用 kmp ,计算 A 的 net 数组,然后用 B 去比较
代码:
#include<bits/stdc++.h>
#define re register int
typedef unsigned long long ull;
using namespace std;
const int N=1e6+10;
const int mo=131;
int t,la,lb;
ull f1[N],f2[N],use[N];
long long maxx;
char s1[N],s2[N];
char ch;
bool pd(int t1,int e1,int t2,int e2)
{
if(((ull)f2[e1]-f1[t1-1]*use[e1-t1+1])==((ull)f1[e2]-f1[t2-1]*use[e2-t2+1]))
return true;
return false;
}
int main()
{
scanf("%d",&t);
use[0]=1;
for(re i=1;i<=N-5;i++)
use[i]=use[i-1]*mo;
while(t--)
{
maxx=0;
memset(f1,0,sizeof(f1));
memset(f2,0,sizeof(f2));
scanf("%d%d",&la,&lb);
scanf("%s",s1+1);
for(re i=1;i<=lb;i++)
{
s2[i]=s1[i];
f2[i]=f2[i-1]*mo+(ull)s2[i];
}
for(re i=1;i<=la;i++)
f1[i]=f1[i-1]*mo+(ull)s1[i];
cin>>ch;
++lb;
s2[lb]=ch;
f2[lb]=f2[lb-1]*mo+(ull)s2[lb];
for(re i=lb;i;i--)
{
int L=lb-i+1;
if(pd(i,lb,1,L)==true)
{
maxx=max(maxx,L*1ll);
if((L==lb)||(L==la))
break;
}
}
printf("%lld\n",maxx);
}
return 0;
}
B. 回家
题目描述



这道题很有迷惑性,乍一看以为就是个 tarjan 求割点的板子(至少我在考场上是这样想的,成功收获了 0 分的好成绩),但其实仔细想想,割点和必经点是有区别的,
如图:
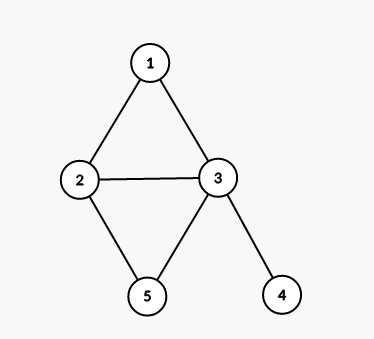
若从1到5,我们注意到 3 为割点,但是不是必经点!!
所以,这道题思路(PTY大佬想出来的)类似于一个双指针,在从 1 号节点 dfs 的同时从 n 号节点往上更新自己属于那颗子树,(因为只有 n 号节点属于的那个子树上的割点才是我们必经点)
具体实现看代码:
#include<bits/stdc++.h>
#define re register int
#define ll long long
#define next net
using namespace std;
const int N=2e6+10;
int t,n,m,tot,top,num,root,gd,out,TOT,col_num,cnt;
int to[N<<1],head[N<<1],next[N<<1],col[N];
int TO[N<<1],HEAD[N<<1],NEXT[N<<1];
int dfn[N],low[N],vis[N],st[N],fa[N][30];
bool ge[N],ge_col[N];
inline int read()
{
char ch=getchar();
int x=0;
while(ch<'0'||ch>'9')
ch=getchar();
while(ch>='0'&&ch<='9')
{
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return x;
}
inline void add(int x,int y)
{
to[++tot]=y;
next[tot]=head[x];
head[x]=tot;
}
inline void tarj(int x)
{
dfn[x]=low[x]=++num;
for(re i=head[x];i;i=next[i])
{
int p=to[i];
if(!dfn[p])
{
tarj(p);
low[x]=min(low[x],low[p]);
if(vis[p]==1)
vis[x]=1;
if(low[p]>=dfn[x]&&vis[p]&&x!=1) //注意此处是 vis[p],而不是 vis[x],以为只有从下面回溯回来的才是正确的,或者,这个节点已经被更新过了,不能再次参与计算!!
{
++cnt;
ge[x]=1;
}
}
else
low[x]=min(low[x],dfn[p]);
}
}
inline void in()
{
memset(to,0,sizeof(to));
memset(head,0,sizeof(head));
memset(next,0,sizeof(next));
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
memset(vis,0,sizeof(vis));
memset(ge,0,sizeof(ge));
num=0;
tot=0;
out=0;
cnt=0;
}
int main()
{
t=read();
//cin>>t;
while(t--)
{
in();
n=read();
m=read();
int a,b;
for(re i=1;i<=m;i++)
{
a=read();
b=read();
add(a,b);
add(b,a);
}
vis[n]=1;
tarj(1);
if(!cnt)
{
printf("0\n");
printf("\n");
continue;
}
printf("%d\n",cnt);
for(re i=2;i<n;i++)
if(ge[i])
printf("%d ",i);
printf("\n");
}
return 0;
}
C. 寿司
题目描述


考场上看到这道题,没什么好思路,只想到一种贪心做法,就是将相邻的字母合并,计算 size 然后将小的合并到大的上去,得了15分;
这道题正解应该是考虑这样一个式子,我们以 R 为例,令 l[i] 表示 R 左边的 B 的数量, r[i] 表示 R 右边的 B 的数量 ,
以 R 为例,那么我们要求 $min\sum\limits_{i=1}^{tot_R}\min(l_i,r_i)$
我们对这个式子进行化简,可得$min\sum\limits_{i=1}^{tot_R}(\frac{(l[i]+r[i]-|l[i]-r[i]|)}{2})$
进一步 $((l[i]+r[i])/2)-\sum\limits_{i=1}^{tot_R}\max(\frac{(|l[i]-r[i]|)}{2})$
简单来说,就是如下式子:
$$tot_R*tot_B-\sum\limits_{i=1}^{tot_R}\max(\dfrac{|l[i]-r[i]|}{2})$$
所以,我们就把这个 (|l[i]-r[i]|)/2 , 拎出来搞一搞,如何求出最大值?
我们针对一个给出的序列,如 BBRBBRBBBRRR ,那么我们就让它动起来(感性理解一下),首先计算出每个 R 左右两侧的 B 的个数,然后通过一个小根堆维护一个 (l[i]-r[i])的值,计算出 (l[i]-r[i]) 为正的个数 zh ,非正数(包括零)的个数为 fu,
我们按顺序枚举每一位 s ,将其放到序列末尾
若 s[i]==B ,则 ++use (记录移动的 B 的数量),sum(记录最大值) sum+=fu*2,
(这里应该比较好理解,将一个 B 放到了末尾,左边的贡献 -1,右边的贡献 +1,所以 sum 保存的是绝对值 ,要+=2),然后进入队列进行更新,最后 sum-=(zh*2),这里同理,因为他们的差值的绝对值在减小,更新 maxx ;
若 s[i]==R,则 q.push(tot_B+2*use), 解释一下就是我放进队列的都是每个 R 左右两侧的贡献,这个 R 放到了最右面那么贡献就是 tot_B ,还要加上 2*use ,因为计算时要累乘 use ,到这里应该解释的差不多了,
结合代码应该可以理解透彻
#include<bits/stdc++.h>
#define re register int
#define ll long long
using namespace std;
const ll N=1e6+10;
ll t,len,sum,maxx;
ll rs,bs,use,zh,fu;
ll l[N],r[N];
char s[N];
priority_queue<ll,vector<ll>,greater<ll> > q;
void in()
{
zh=0;
fu=0;
bs=0;
rs=0;
sum=0;
maxx=0;
use=0;
memset(l,0,sizeof(l));
memset(r,0,sizeof(r));
while(!q.empty())
q.pop();
}
int main()
{
scanf("%lld",&t);
while(t--)
{
scanf("%s",s+1);
len=strlen(s+1);
in();
for(re i=1;i<=len;i++)
{
l[i]=l[i-1];
if(s[i]=='R')
{
l[i]=bs;
++rs;
}
else
++bs;
}
for(re i=1;i<=len;i++)
{
if(s[i]=='R')
{
r[i]=bs-l[i];
if(l[i]-r[i]>0)
{
q.push(l[i]-r[i]);
//cout<<(l[i]-r[i])<<" i="<<i<<" l[i]="<<l[i]<<" r[i]="<<r[i]<<endl;
++zh;
}
else
++fu;
sum+=abs(l[i]-r[i]);
}
}
/*for(re i=1;i<=len;i++)
cout<<l[i]<<" "<<r[i]<<endl;*/
maxx=sum;
for(re i=1;i<=len;i++)
{
if(s[i]=='B')
{
++use;
sum+=fu*2;
while(!q.empty())
{
if(q.top()-(use<<1)>0)
break;
if(q.top()-(use<<1)==0)
sum-=2;
fu++;
zh--;
q.pop();
}
sum-=(zh<<1);
maxx=max(maxx,sum);
}
else
{
q.push(bs+(use<<1));
++zh;
--fu;
}
}
printf("%lld\n",(bs*rs-maxx)>>1);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号