内存限制:64 MiB 时间限制:1000 ms 标准输入输出
题目类型:传统 评测方式:文本比较
辣鸡ljh NOI之后就退役了,然后就滚去学文化课了。
然而在上化学课的时候,数学和化学都不好的ljh却被一道简单题难住了,受到了大佬的嘲笑。
题目描述是这样的:
在一个二维平面上有一层水分子,请问形成了多少个氢键?
这个二维平面可以看做一个类似棋盘的东西,每个格子可以容纳一个水分子,左下角的格子为(0,0),这个格子右边的格子为(1,0),上方格子为(0,1),以此类推。
辣鸡ljh当然不会做了,所以他来求助JeremyGou,JeremyGou一眼就看穿了真相,并想用这道题来考一考正在做NOIP模拟赛的你。
注:在本题中,我们认为一个水分子能与和它曼哈顿距离为2且直线距离小于2的其他格子形成氢键。
一个整数n
接下来n行,每行给出四个整数x1,y1,x2,y2
表示以(x1,y1)为左下角,(x2,y2)为右上角的矩形中每个格子都有一个水分子。
给出的所有矩形没有交集。
样例输入1
3
0 0 0 0
0 1 1 2
2 2 2 3
样例输出1
样例1解释
左图为水分子的排布,右图中的绿色线条表示氢键。

样例输入2
10
1 8 8 9
0 3 10 7
0 0 7 0
0 2 9 2
4 10 8 10
10 0 10 2
0 10 0 10
8 0 9 1
0 8 0 9
9 8 10 8
样例输出2
析:刚开始看到这道题,不知道什么是曼哈顿距离,解释一下:在平面上,坐标(x1,y1)的i点与坐标(x2,y2)的j点的曼哈顿距离为:d(i,j)=|X1-X2|+|Y1-Y2|.
所以,我们要求的就是四个方向上可以连成的氢键;
在考场上,我看到一个N=1的测试点,找到了规律:一个矩形内部的氢键个数为 (x2-x1)*(y2-y1)*2,5分到手。。。。。。。
当时我还打了个暴力dfs,应该是边界条件问题打假了;
正解为大模拟,将答案分为四部分:1.每个矩形内部的氢键。2.矩形左右相邻的氢键。3.矩形上下相邻的氢键。4.矩形对角线相邻的氢键,利用sort排序后模拟即可
上代码:
#include<bits/stdc++.h>
#define re register int
#define ll long long
#define int long long
using namespace std;
const int N=1e9+5;
int n,cnt,sum,ans;
map<pair<int,int>,bool> p;
struct CUN
{
int x1,y1,x2,y2;
}use[2000010];
int my(CUN a,CUN b)
{
if(a.x1==b.x1)
return a.y1<b.y1;
return a.x1<b.x1;
}
#undef int
int main()
{
#define int long long
scanf("%lld",&n);
int x1,y1,x2,y2;
for(re i=1;i<=n;i++)
{
scanf("%lld%lld%lld%lld",&x1,&y1,&x2,&y2);
ans+=((x2-x1)*(y2-y1))<<1;
use[i].x1=x1;
use[i].y1=y1;
use[i].x2=x2;
use[i].y2=y2;
}
sort(use+1,use+n+1,my);
for(re i=1;i<n;i++)
{
for(re j=i+1;j<=n;j++)
{
if(use[j].x1-use[i].x2>1)
break;
if(use[j].y2<use[i].y1-1||use[j].y1>use[i].y2+1)
continue;
if(use[j].x1<=use[i].x2) //上下相邻
{
if(use[i].x1==use[j].x1)
{
if(use[i].x2==use[j].x2)
ans+=use[i].x2-use[i].x1;
else if(use[j].x2>use[i].x2)
ans+=((use[i].x2-use[i].x1)<<1)+1;
else if(use[i].x2>use[j].x2)
ans+=((use[j].x2-use[j].x1)<<1)+1;
}
else if(use[i].x2==use[j].x2)
{
if(use[i].x1==use[j].x1)
ans+=use[i].x2-use[i].x1;
else if(use[i].x1>use[j].x1)
ans+=((use[i].x2-use[i].x1)<<1)+1;
else if(use[j].x1>use[i].x1)
ans+=((use[j].x2-use[j].x1)<<1)+1;
}
else if(use[i].x2>use[j].x2)
ans+=(use[j].x2-use[j].x1+1)<<1;
else
ans+=(use[i].x2-use[j].x1+1)<<1;
}
else //左右
{
if(abs(use[j].y1-use[i].y2)==1)//对角线
++ans;
else if(use[i].y1==use[j].y1)
{
if(use[i].y2==use[j].y2)
ans+=use[i].y2-use[i].y1;
else if(use[j].y2>use[i].y2)
ans+=((use[i].y2-use[i].y1)<<1)+1;
else if(use[i].y2>use[j].y2)
ans+=((use[j].y2-use[j].y1)<<1)+1;
}
else if(use[i].y2==use[j].y2)
{
if(use[i].y1==use[j].y1)
ans+=use[i].y2-use[i].y1;
else if(use[i].y1>use[j].y1)
ans+=((use[i].y2-use[i].y1)<<1)+1;
else if(use[j].y1>use[i].y1)
ans+=((use[j].y2-use[j].y1)<<1)+1;
}
else if(use[i].y2>use[j].y2)
ans+=(use[j].y2-use[j].y1+1)<<1;
else
ans+=(use[i].y2-use[j].y1+1)<<1;
}
}
}
printf("%lld\n",ans);
return 0;
}
内存限制:512 MiB 时间限制:1000 ms 标准输入输出
题目类型:传统 评测方式:文本比较
辣鸡ljh NOI之后就退役了,然后就滚去学文化课了。
他每天都被katarina大神虐,仗着自己学过一些姿势就给katarina大神出了一道题。
有一棵 n 个节点的以 1 号节点为根的树,每个节点上有一个小桶,节点u上的小桶可以容纳
个小球,ljh每次可以给一个节点到根路径上的所有节点的小桶内放一个小球,如果这个节点的小桶满了则不能放进这个节点,在放完所有小球之后就企图去刁难katarina大神,让katarina大神回答每个节点的小桶内的小球有多少种颜色。
然而katarina大神一眼就秒掉了,还说这就是一道傻逼模板题。
现在katarina大神想考考即将参加NOIP2019的你能不能回答上辣鸡ljh的问题。
第一行,一个整数n,树上节点的数量。
接下来n ? 1行,每行两个整数u, v,表示在u, v之间有一条边。
接下来一行n个整数,
~
表示每个节点上的小桶数量。
下一行是一个整数m,表示ljh进行的操作数量。
接下来m行,每行两个整数x, c,分别表示进行操作的节点和小球颜色。
下一行是一个整数Q,表示你需要回答的询问数。
接下来Q行,每行一个整数x,表示一个询问。
样例输入1
5
1 2
2 3
3 4
2 5
2 1 1 1 1
2
2 1
4 2
3
1
3
5
样例输出1
样例输入2
10
3 10
2 5
3 2
2 6
1 9
8 7
7 4
3 8
3 1
15 47 23 22 9 16 45 39 21 13
10
10 7
9 3
5 1
5 2
9 4
10 9
2 4
10 1
2 6
7 9
3
1
2
3
样例输出2
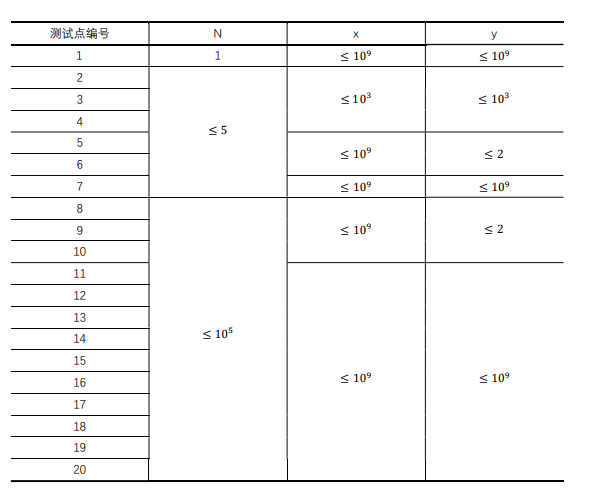
子任务

析:这道题的暴力很好想,在考场上我理论上能拿30分(看错题了。。。,颜色相同的点不算贡献,但是会算空间!!!),正解应该是线段树合并,这个先留着
内存限制:512 MiB 时间限制:1000 ms 标准输入输出
题目类型:传统 评测方式:文本比较
辣鸡ljh NOI之后就退役了,然后就滚去学文化课了。
他发现katarina大佬真是太强了,于是就学习了一下katarina大佬的做题方法。
比如这是一本有n道题的练习册,katarina大佬每天都会做k道题。
第一天做第1~k题,第二天做第
~
题……第
天做第
~
道题。
但是辣鸡 ljh 又不想太累,所以他想知道katarina大佬做完这本练习册的劳累度。
每道题有它的难度值,假设今天katarina大佬做的题目中最大难度为t,那么今天katarina大佬的劳累度就是wt?,做完这本书的劳累值就是每天的劳累值之和。
但是辣鸡ljh一道题都不会,自然也不知道题目有多难,他只知道题目的难度一定在1~m之间随机。
他想让即将参加 NOIP 的你帮他算算katarina大佬做完这本书的劳累值期望
第二行,
个整数表示
样例输入1
样例输出1
样例1解释
有{1,1},{1,2},{2,1},{2,2}四种可能,期望为
子任务

析:很明显的一道概率期望题,在考场上我想了2个小时左右,但是思路想偏了,我当时一直在想第 i 小的值作为最大值的概率,但是正解应该为 第 i 天的值作为最大值的概率 p=(x/m)^k , 具体来说就是 f[1]=(1\m)^k , f[2]=(2\m)^k-f[1] , f[3]=(3/m)^k-f[2]-f[1]......
所以结果为 (i (1->m) sum(w[i]*f[i]) )*(n-k+1);
注意最后取模的时候要先给 ans * inv ,再取模,不然会出错!!
代码:
#include<bits/stdc++.h>
#define re register int
#define D double
#define int long long
#define mo 1000000007
using namespace std;
const int N=610;
int n,m,k,tot,cnt;
int ans,inv,cj,s;
int f[N],w[N],cf[N];
int ksm(int d,int z)
{
int out=1;
while(z)
{
if(z&1)
out=out*d%mo;
z>>=1;
d=d*d%mo;
}
return out;
}
#undef int
int main()
{
#define int long long
scanf("%lld%lld%lld",&n,&m,&k);
for(re i=1;i<=m;i++)
scanf("%lld",&w[i]);
if(k>n)
{
printf("0\n");
return 0;
}
cj=ksm(m,k);
inv=ksm(cj,mo-2);
for(re i=1;i<=m;i++)
{
f[i]=(ksm(i,k)-s)%mo;
s=s+f[i]%mo;
}
for(re i=1;i<=m;i++)
ans=(ans%mo+w[i]*f[i])%mo;
ans=((ans*inv)%mo*((n-k+1)%mo))%mo;
printf("%lld\n",(ans+mo)%mo);
return 0;
}



析:看到数据范围,妥妥的状压dp,但是这道题是 dp+dfs,思路 f[j][(1<<(j-1))|s][deep+1]=min(sum+dis[i]*l[i][j]) , 表示将节点 j 放入集合 s 中,从 i (深度为deep)转移过来的最小值;
注意在dfs 过程中要用两层 for 循环来枚举从哪里转移过来,并保存 dis[x],为经过的节点数,因为从哪个点转移来的不确定,所以这个值不能直接传到函数里!!
注意dfs里四个剪枝优化,看似不起眼但是效果巨大!!
代码:
#include<bits/stdc++.h>
#define re register int
#define next net
using namespace std;
const int N=1010;
const int INF=1e9;
int n,m,tot,ans=INF;
int l[15][15],f[15][1<<13][13];//!!!
int to[15][15],dis[15];
map<int,bool> p[15];
void dfs(int s,int deep,int sum)
{
if(sum>=ans)
return;
if(s==((1<<n)-1))
{
ans=min(ans,sum);
//cout<<"deep="<<deep<<" ans="<<ans<<endl;
return;
}
//int cun=0;
for(re i=1;i<=n;i++)
{
if(!(s&(1<<(i-1))))
continue;
for(re j=1;j<=n;j++)
{
if(s&(1<<(j-1)))
continue;
if(f[j][s|(1<<(j-1))][deep+1]<=sum+dis[i]*l[i][j])
continue;
if(!p[i][j])
continue;
f[j][s|(1<<(j-1))][deep+1]=sum+dis[i]*l[i][j];
//cout<<"i="<<i<<" j="<<j<<" f="<<f[j][s|(1<<(j-1))][deep+1]<<endl;
dis[j]=dis[i]+1;
dfs(s|(1<<(j-1)),deep+1,f[j][s|(1<<(j-1))][deep+1]);
}
}
}
int main()
{
int a,b,c;
scanf("%d%d",&n,&m);
memset(l,127,sizeof(l));
for(re i=1;i<=m;i++)
{
scanf("%d%d%d",&a,&b,&c);
if(!p[a][b])
{
p[a][b]=1;
to[a][++to[a][0]]=b;
p[b][a]=1;
to[b][++to[b][0]]=a;
}
l[a][b]=min(l[a][b],c);
l[b][a]=l[a][b];
}
for(re i=1;i<=n;i++)
{
memset(f,127,sizeof(f));
memset(dis,0,sizeof(dis));
dis[i]=1;
//f[i][1<<(i-1)][1]=0;
dfs((1<<(i-1)),0,0);
}
printf("%d\n",ans);
return 0;
}









 浙公网安备 33010602011771号
浙公网安备 33010602011771号