排序算法 - 计数排序
基本思想
计数排序是一种线性排序算法，它利用了一个数组，因为数组下标的增长是线性的，所以它就把自己的元素转换成新开辟数组的下标。可是下标都是非负数啊？数组当中的值有正有负啊。做一个简单的转化就行了：找到数组中最小元素，用元素值减去，这样一来，所有元素对应的下标就求出来了。（实际上感觉像是个映射函数？）下图中保存的是待排序数组：[-1,-5,-6,-2,1,2,8,2,1,8]
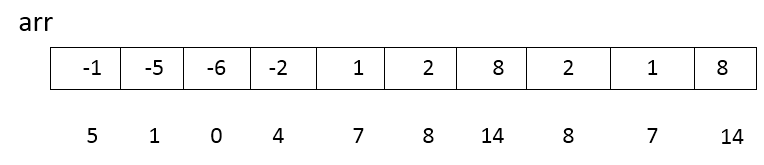
然后跟哈希排序的思路一样：这里。直接开辟一个对应的哈希数组，然后统计每个元素出现的次数。橙色标注出来的表示待排序数组中没有的元素（转换后的元素），自然就没有出现次数。这样可以看出来如果数组中元素差距很大，其实还是很浪费空间的，因为它新开辟数组的大小是待排序数组arr中max-min+1（8+6+1=15）。
最后再将count中的元素放回到arr中，就完成排序了。
算法代码
1 //计数排序 2 void CountSort(int *a, int size) 3 { 4 int max = a[0]; 5 int min = a[0]; 6 for (int i = 0; i < size; ++i) 7 { 8 if (a[i] > max) 9 max = a[i]; 10 if (a[i] < min) 11 min = a[i]; 12 } 13 int range = max - min + 1; //要开辟的数组范围 14 int *count = new int[range]; 15 memset(count, 0, sizeof(int) * range); //初始化为0 16 //统计每个数出现的次数 17 for (int i = 0; i < size; ++i) //从原数组中取数，原数组个数为size 18 { 19 count[a[i] - min]++; 20 } 21 //写回到原数组 22 int index = 0; 23 for (int i = 0; i < range; ++i) //从开辟的数组中读取，开辟的数组大小为range 24 { 25 while (count[i]--) 26 { 27 a[index++] = i + min; 28 } 29 } 30 delete[] count; 31 }
算法分析
计数排序是一种非基于比较的排序算法，其空间复杂度和时间复杂度均为 O(n+k)，其中 k 是整数的范围。
[参考：https://blog.csdn.net/qq_34269988/article/details/90705977]
