排序算法 - 基数排序
基本思想
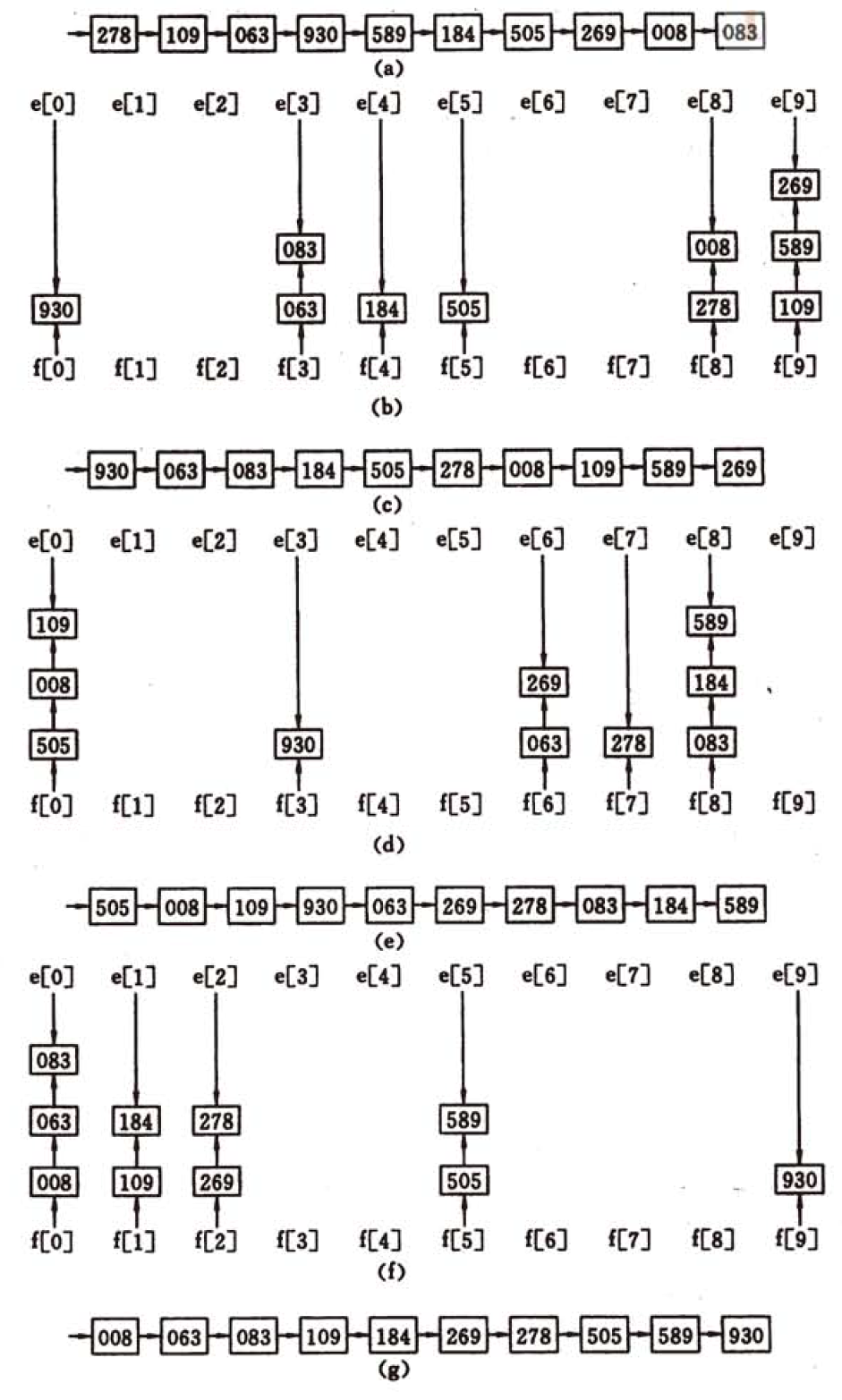
基数排序是借助“分配”和“收集”两种操作对单逻辑关键字进行排序的一种内部排序方法。
数组下标从0-9，每个数组元素是一个链表
比如对一些三位数以内的树排序，先将个位的数值插入对应的下标的链表中，然后再放回原数组，放回的顺序和插入的顺序一致，将链表清空，再将十位的数字插入对应的下标的链表中，依次操作，最终数组中的数据便以完成排序。
算法代码
1 //基数排序 2 int GetKey(int value, int k) //获取一个数的第k位数字 3 { 4 int key; 5 while (k > 0) 6 { 7 key = value % 10; 8 value /= 10; 9 k--; 10 } 11 return key; 12 } 13 14 void Distribube(int *arr, int n, int k, list<int> *lists) //分配 15 { 16 for (int i = 0; i < n; ++i) 17 { 18 int index = GetKey(arr[i], k); 19 lists[index].push_back(arr[i]); 20 } 21 } 22 23 void Collect(int *arr, list<int> *lists) //收集 24 { 25 int index = 0; 26 list<int>::iterator it; 27 for (int i = 0; i < 10; ++i) 28 { 29 it = lists[i].begin(); 30 while (it != lists[i].end()) 31 { 32 arr[index++] = *it; 33 ++it; 34 } 35 lists[i].clear(); //收集完成要清空链表 36 } 37 } 38 39 void RadixSort(int *arr, int n) 40 { 41 int k = 3; //对1000以内的数进行排序 42 list<int> lists[10]; //从0-9共10个链表 43 for (int i = 1; i <= 3; ++i) 44 { 45 Distribube(arr, n, i, lists); //三位数分发三次，每次都会插入对应的链表中 46 Collect(arr, lists); //每一次将链表中的数据都会被重新放在数组中 47 } 48 }
算法分析
基数排序的时间复杂度为O(d(n+r))
其中：分配为O(n)
收集为O(r)（r为“基数”）
d为“分配-收集”的趟数
基数排序的空间复杂度为O(r)
属于稳定的排序算法
