排序算法 - 希尔排序
基本思路
希尔排序也是一种插入排序,又称缩小增量排序,在效率上教其他插入排序有较大的改进。
① d=n/2
②将排序序列分为d个组,在各组内进行直接插入排序
③递减d=d/2,重复② ,直到d=1
算法最后一趟对所有数据进行了直接插入排序,所以结果一定是正确的。
它的基本思想是:先将整个待排记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
一趟希尔排序过程
将记录序列分成若干子序列,分别对每个子序列进行直接插入排序。
例如:将 n 个记录分成 d 个子序列:

例子:
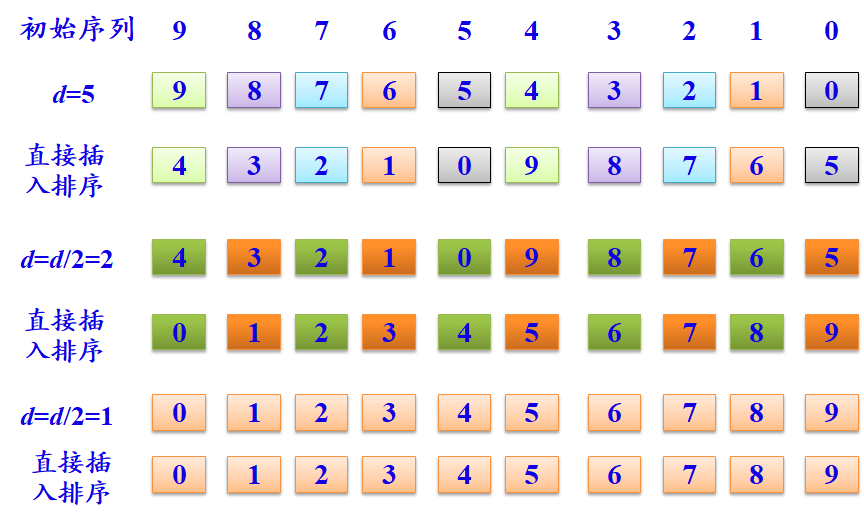
注意:对于d=1的一趟,排序前的数据已将近正序!
希尔排序的分析是一个复杂的问题,因为它的时间是所取“增量”序列的函数,这涉及一些数学上尚未解决的难题。因此,到目前为止尚未有人求得一种最好的增量序列,但大量的研究已得出一些局部的结论。如有人指出,当增量序列为![]() 时,希尔排序的时间复杂度为
时,希尔排序的时间复杂度为![]() ,其中t为排序趟数,
,其中t为排序趟数,![]() 。需注意:应使增量序列中的值没有除1之外的公因子,并且最后一个增量值必须等于1。
。需注意:应使增量序列中的值没有除1之外的公因子,并且最后一个增量值必须等于1。
为了便于阅读,本例增量直接采用除2法。
算法代码
1 //希尔排序 2 void ShellSort(int *arr, int n) 3 { 4 int i, j; 5 int temp; 6 int d = n / 2; //增量初始值 7 while (d > 0) //每次循环减小增量 8 { 9 for (i = d; i < n; i++) //当超过了2*d时候,后面的会继续和前面的组的元素比较,后面不论是多少个元素,是否是倍数都不影响 10 { 11 temp = arr[i]; //对相隔d位置的元素组直接插入排序 12 for (j = i - d; j >= 0 && temp < arr[j]; j -= d) 13 { 14 arr[j + d] = arr[j]; 15 } 16 arr[j + d] = temp; 17 } 18 d = d / 2; //减小增量 19 } 20 }
算法分析
希尔排序是一种不稳定的排序算法,时间复杂度约为O(n1.3)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号