排序算法 - 插入排序

直接插入排序

 基本思路

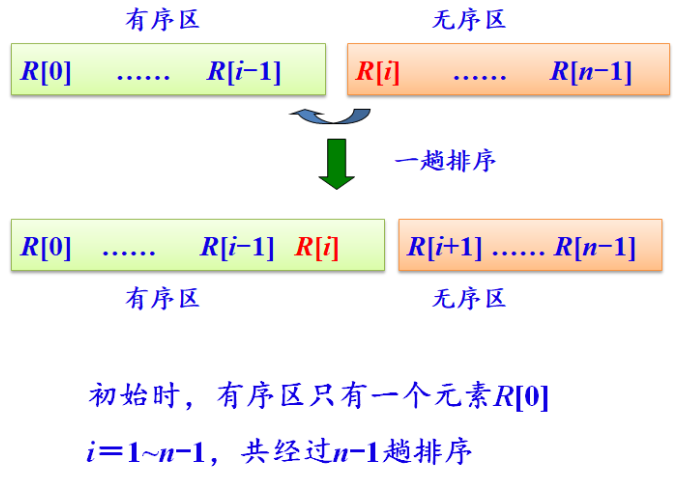
一趟直接插入排序：在有序区中插入R[i]的过程。

 

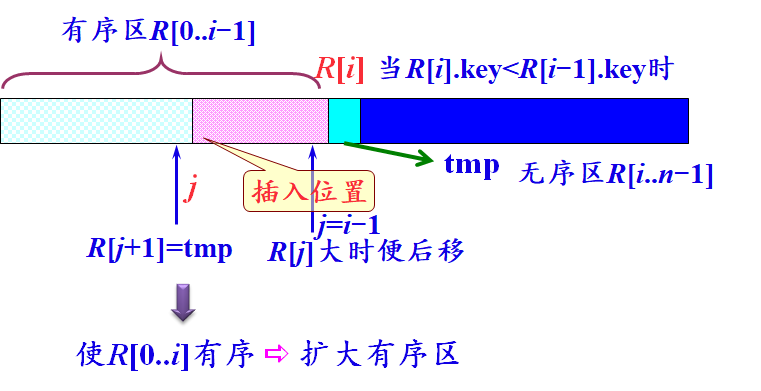
算法代码

//直接插入排序
void InsertSort(int *arr, int n)
{
    int i, j;
    int temp;

    for (i = 1; i < n; i++)
    {
        if (arr[i] < arr[i - 1]) //如果第i个和前面的已排序的最后一个元素反序时,才开始移动
        {
            temp = arr[i]; //记住这个元素
            for (j = i - 1; j >= 0 && arr[j] > temp; j--)
            {
                arr[j + 1] = arr[j]; //将比temp大的元素统一向后移动
            }
            arr[j + 1] = temp; //在条件不满足之前j--了一次，在j+1处放入temp
        }
    }
}

算法分析

折半插入排序

 基本思路

 直接插入排序，当有序区元素太多时，在有序区中寻找插入位置可能比较的次数太多，采用折半插入法，即折半查找到要插入的位置，加快了查找效率，但是要移动的元素仍然和直接插入排序的相同，仅仅提升了查找效率。

 

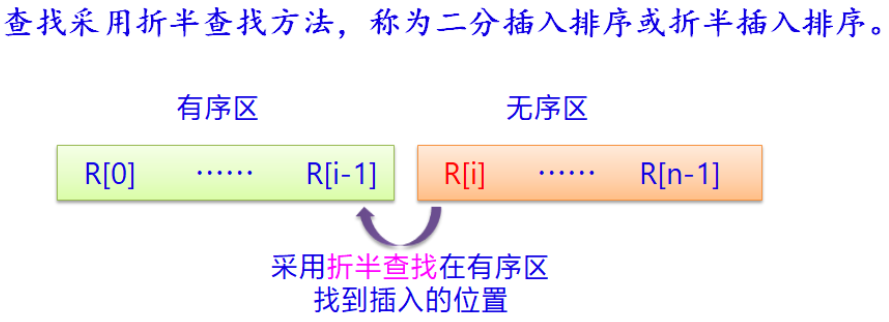
算法代码

//折半插入排序
void BinInsertSort(int *arr, int n)
{
    int i, j;
    int low, high, mid;
    int temp;
    for (i = 1; i < n; i++)
    {
        if (arr[i] < arr[i - 1]) //如果第i个和前面的已排序的最后一个元素反序时,才开始查找
        {
            temp = arr[i]; //将要插入的元素被temp记住
            low = 0;
            high = i - 1;

            while (low <= high)
            {
                mid = (low + high) / 2;
                if (temp < arr[mid])
                    high = mid - 1;
                else
                    low = mid + 1;
            } //找到位置high

            for (j = i - 1; j >= high + 1; j--) //将比temp大的元素统一向后移动
            {
                arr[j + 1] = arr[j];
            }
            arr[high + 1] = temp; //在high+1处放入temp
        }
    }
}

 算法分析

折半插入排序：在R[0..i-1]中查找插入R[i]的位置，折半查找的平均关键字比较次数为log2(i+1)-1，平均移动元素的次数为i/2+2，所以平均时间复杂度为：

 

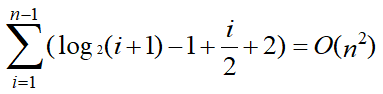
折半插入排序采用折半查找，查找效率提高。但元素移动次数不变，仅仅将分散移动改为集合移动。