【二叉搜索树】的详细实现(C++)
二叉搜索树的概念
从前面讨论折半搜索的性能中可知,如果每次从搜索序列的中间进行搜索,把区间缩小一半,通过有限次迭代,很快就能通近到所要寻找的元素。进一步,如果我们直接输入搜索序列,构造出类似于折半搜索的判定树那样的树形结构,就能实现快速搜索。这种树形结构就是二又搜索树。
二又搜索树(binary search tree)或者是一棵空树,或者是具有下列性质的二又树:
(1)每个结点都有一个作为搜索依据的关键码(key),所有结点的关键码互不相同。
(2)左子树(如果存在)上所有结点的关键码都小于根结点的关键码。
(3)右子树(如果存在)上所有结点的关键码都大于根结点的关键码。
(4)左子树和右子树也是二又搜索树。
关键码事实上是结点所保存元素中的某个域的值,它能够唯一地表示这个结点。因此,如果对一棵二又搜索树进行中序遍历,可以按从小到大的顺序,将各结点关键码排列起来,所以也称二叉搜索树为二又排序树(binary sorting tree)。
二叉搜索树的建立
输入一系列数据,建立一棵二又搜索树。它要求从空树开始建树,输入序列以输入一个结束标志value结束。这个值应当取不可能在输入序列中出现的值,例如输入序列的值都是正整数时,取RefValue为0或负数。
1 //构造BST 2 BST(T value) :root(NULL), RefValue(value) 3 { 4 T x; 5 cin >> x; 6 while (x != RefValue) 7 { 8 Insert(x, root); //新建一个结点,调用Insert插入到树中 9 cin >> x; 10 } 11 }
二叉搜索树的插入
为了向二又搜索树中插入一个新元素,必须先检查这个元素是否在树中已经存在。所以在插入之前,先使用搜索算法在树中检查要插入元素有还是没有。如果搜索成功,说明树中已经有这个元素,不再插入;如果搜索不成功,说明树中原来没有关键码等于给定值的结点,把新元素加到搜索操作停止的地方。当ptr!=NULL时,它一定指向一棵子树的根,可用它所包含的关键码与给定值比较继续搜索插入位置;如果 ptr=NULL,一定是递归到空树的位置,此时将创建的新结点地址送给ptr,因为ptr是引用,新结点的地址自然送入上述某一个指针域,自动将新结点作为叶结点链入二又搜索树中了。每次结点的插入,都要从根结点出发搜索插入位置,然后把新结点作为时结点插入。这样不需移动结点,只需修改某个已有树中结点的一个空指针即可。
1 //以ptr为根的二叉搜索树中插入所含值为e1的结点 2 bool Insert(const T& e1, BSTNode<T>* &ptr) //第二个参数是指针的引用 3 { 4 if (ptr == NULL) 5 { 6 ptr = new BSTNode<T>(e1); //构造新结点 7 if (ptr == NULL) 8 { 9 cout << "Memory allocation failed!" << endl; 10 exit(1); 11 } 12 return true; 13 } 14 else if (e1 < ptr->data) //小于,插入左子树 15 { 16 Insert(e1, ptr->left); 17 } 18 else if (e1 > ptr->data) //大于,插入右子树 19 { 20 Insert(e1, ptr->right); 21 } 22 else //x已在树中,不插入 23 { 24 return false; 25 } 26 }
二叉搜索树的递归搜索
从根结点开始,沿某一个分支逐层向下进行比较判等的过程。它可以是一个递归的过程。假设想要在二又搜索树中搜索关键码为x的元素,搜索过程从根结点开始。如果根指针为NULL,则搜索不成功;否则用给定值x与根结点的关键码进行比较:如果给定值等于根结点的关键码,则搜索成功,返回搜索成功信息,并报告搜索到的结点地址。如果给定值小于根结点的关键码,则继续递归搜索根结点的左子树,否则,递归搜索根结点的右子树。
1 //在ptr为根的二叉搜索树中搜索含x的结点。若找到,返回该结点地址,否则返回NULL 2 BSTNode<T>* Search(T x, BSTNode<T>* ptr) 3 { 4 if (ptr == NULL) 5 { 6 return NULL; 7 } 8 else if (x < ptr->data) 9 { 10 return Search(x, ptr->left); 11 } 12 else if (x > ptr->data) 13 { 14 return Search(x, ptr->right); 15 } 16 else 17 { 18 return ptr; 19 } 20 }
二叉搜索树的删除
在二又搜索树中删除一个结点时,必须将因删除结点而断开的二又链表重新链接起来,同时确保二叉搜索树的性质不会失去。此外,为了保证在执行删除后,树的搜索性能不至于降低,还需要防止重新链接后树的高度不能增加。
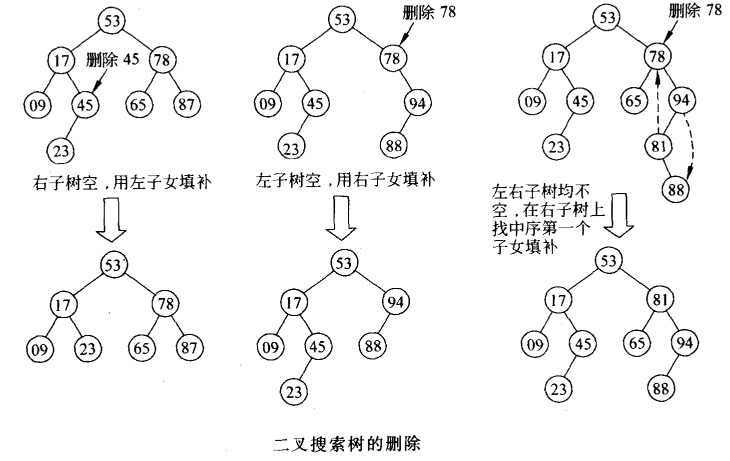
如果想要删除叶结点,只需将其父结点指向它的指针清零,再释放它即可。
如果被删结点右子树为空,可以拿它的左子女结点顶替它的位置,再释放它。
如果被删结点左子树为空,可以拿它的右子女结点顶替它的位置,再释放它。
如果被删结点左、右子树都不空,可以在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删结点中,再来处理这个结点的删除问题,这是一个递归处理。例如,在上图中想要删除关键码为78的结点,它的左、右子树都不空。在它的右子树中找中序下的第一个结点,其关键码为81。把它的值填补到被删结点中去,下面的问题就是删除关键码为81的结点了。这个结点左子树为空,用它的右子女(关键码为88)代替它的位置就可以了。
1 //以ptr为根的二叉搜索树中删除含x的结点 2 bool Remove(T x, BSTNode<T>* &ptr) 3 { 4 BSTNode<T>* temp; 5 if (ptr != NULL) //ptr不为空进行操作 6 { 7 if (x < ptr->data) 8 { 9 Remove(x, ptr->left); 10 } 11 else if (x > ptr->data) 12 { 13 Remove(x, ptr->right); 14 } 15 //找到了要删除的结点 16 //1.要删除的结点ptr同时有左右子树 17 else if (ptr->left != NULL&&ptr->right != NULL) 18 { 19 temp = ptr->right; //在右子树中搜索中序下的第一个结点 20 while (temp->left != NULL) 21 { 22 temp = temp->left; 23 } 24 //用右子树中序下的第一个结点的值填充要删除的结点 25 ptr->data = temp->data; 26 //然后再新填充值ptr的右子树中删除temp的data值 27 Remove(ptr->data, ptr->right); 28 } 29 else //不同时有左右子树 30 { 31 temp = ptr; //temp记住要删除的ptr结点 32 if (ptr->left == NULL) //只有右子树 33 { 34 ptr = ptr->right; 35 } 36 else //只有左子树 37 { 38 ptr = ptr->left; 39 } 40 delete temp; //删除结点 41 temp = NULL; 42 return true; 43 } 44 } 45 else //ptr为空直接返回false 46 { 47 return false; 48 } 49 }
二叉搜索树的销毁
二叉搜索树的销毁与普通二叉树基本相同。
1 //销毁以root为根的二叉树搜索树函数 2 void Destroy(BSTNode<T>* &root) 3 { 4 if (root == NULL) 5 { 6 return; 7 } 8 if (root->left != NULL) 9 { 10 Destroy(root->left); 11 } 12 if (root->right != NULL) 13 { 14 Destroy(root->right); 15 } 16 delete root; 17 root = NULL; 18 }
二叉搜索树的源码

1 //二叉搜索树结点类型 2 template<typename T> 3 struct BSTNode 4 { 5 T data; //数据域 6 BSTNode<T> *left, *right; //左子女、右子女 7 BSTNode() :left(NULL), right(NULL) {} //构造函数 8 //构造函数 9 BSTNode(const T d, BSTNode<T>* L = NULL, BSTNode<T>* R = NULL) :data(d), left(L), right(R) {} 10 }; 11 12 //二叉搜索树的定义 13 template <class T> 14 class BST 15 { 16 public: 17 //普通构造函数 18 BST() :root(NULL) {} 19 //构造BST 20 BST(T value) :root(NULL), RefValue(value) 21 { 22 T x; 23 cin >> x; 24 while (x != RefValue) 25 { 26 Insert(x, root); //新建一个结点,调用Insert插入到树中 27 cin >> x; 28 } 29 } 30 //析构 31 ~BST() { Destroy(root); } 32 33 //插入 34 bool Insert(T x) { return Insert(x, root); } 35 36 //删除 37 bool Remove(T x) { return Remove(x, root); } 38 39 //搜索 40 bool Search(T x) { return (Search(x, root) != NULL) ? true : false; } 41 42 //中序遍历 43 void InOrder() { InOrder(root); } 44 45 protected: 46 47 //以ptr为根的二叉搜索树中插入所含值为e1的结点 48 bool Insert(const T& e1, BSTNode<T>* &ptr) //第二个参数是指针的引用 49 { 50 if (ptr == NULL) 51 { 52 ptr = new BSTNode<T>(e1); //构造新结点 53 if (ptr == NULL) 54 { 55 cout << "Memory allocation failed!" << endl; 56 exit(1); 57 } 58 return true; 59 } 60 else if (e1 < ptr->data) //小于,插入左子树 61 { 62 Insert(e1, ptr->left); 63 } 64 else if (e1 > ptr->data) //大于,插入右子树 65 { 66 Insert(e1, ptr->right); 67 } 68 else //x已在树中,不插入 69 { 70 return false; 71 } 72 } 73 74 //以ptr为根的二叉搜索树中删除含x的结点 75 bool Remove(T x, BSTNode<T>* &ptr) 76 { 77 BSTNode<T>* temp; 78 if (ptr != NULL) //ptr不为空进行操作 79 { 80 if (x < ptr->data) 81 { 82 Remove(x, ptr->left); 83 } 84 else if (x > ptr->data) 85 { 86 Remove(x, ptr->right); 87 } 88 //找到了要删除的结点 89 //1.要删除的结点ptr同时有左右子树 90 else if (ptr->left != NULL&&ptr->right != NULL) 91 { 92 temp = ptr->right; //在右子树中搜索中序下的第一个结点 93 while (temp->left != NULL) 94 { 95 temp = temp->left; 96 } 97 //用右子树中序下的第一个结点的值填充要删除的结点 98 ptr->data = temp->data; 99 //然后再新填充值ptr的右子树中删除temp的data值 100 Remove(ptr->data, ptr->right); 101 } 102 else //不同时有左右子树 103 { 104 temp = ptr; //temp记住要删除的ptr结点 105 if (ptr->left == NULL) //只有右子树 106 { 107 ptr = ptr->right; 108 } 109 else //只有左子树 110 { 111 ptr = ptr->left; 112 } 113 delete temp; //删除结点 114 temp = NULL; 115 return true; 116 } 117 } 118 else //ptr为空直接返回false 119 { 120 return false; 121 } 122 } 123 124 //在ptr为根的二叉搜索树中搜索含x的结点。若找到,返回该结点地址,否则返回NULL 125 BSTNode<T>* Search(T x, BSTNode<T>* ptr) 126 { 127 if (ptr == NULL) 128 { 129 return NULL; 130 } 131 else if (x < ptr->data) 132 { 133 return Search(x, ptr->left); 134 } 135 else if (x > ptr->data) 136 { 137 return Search(x, ptr->right); 138 } 139 else 140 { 141 return ptr; 142 } 143 } 144 145 //中序遍历 146 void InOrder(BSTNode<T>* root) 147 { 148 if (root != NULL) 149 { 150 InOrder(root->left); 151 cout << root->data << " "; 152 InOrder(root->right); 153 } 154 } 155 156 //销毁以root为根的二叉树搜索树函数 157 void Destroy(BSTNode<T>* &root) 158 { 159 if (root == NULL) 160 { 161 return; 162 } 163 if (root->left != NULL) 164 { 165 Destroy(root->left); 166 } 167 if (root->right != NULL) 168 { 169 Destroy(root->right); 170 } 171 delete root; 172 root = NULL; 173 } 174 private: 175 BSTNode<T>* root; //根指针 176 T RefValue; //输入结束标识 177 }; 178 179 int main(int argc, char* argv[]) 180 { 181 //g a e d f h j i l k # 182 BST<char> tree('#'); 183 tree.InOrder(); 184 cout << endl; 185 cout << tree.Search('e') << endl; 186 cout << tree.Insert('z') << endl; 187 tree.InOrder(); 188 cout << endl; 189 cout << tree.Remove('z') << endl; 190 cout << tree.Remove('j') << endl; 191 tree.InOrder(); 192 cout << endl; 193 return 0; 194 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号