欧拉定理 / 费马小定理证明
主要部分转自百度百科：https://baike.baidu.com/item/欧拉定理
内容：
在数论中，欧拉定理,(也称费马-欧拉定理)是一个关于同余的性质。欧拉定理表明，若n,a为正整数，且n,a互质，则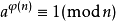
证明：
将1~n中与n互质的数按顺序排布:x1,x2……xφ(n) (显然，共有φ(n)个数)
我们考虑这么一些数:
m1=a*x1;m2=a*x2;m3=a*x3……mφ(n)=a*xφ(n)
说白了就是构造一个群Q,这个群乘上a还是这个群，这样就能做到两个群里的元素相乘相等，约分后得到欧拉定理的那个等式！
(1)
这些数中的任意两个都不模n同余，因为如果有mS≡mR (mod n) (这里假定mS更大一些)，就有:
mS-mR=a(xS-xR)=qn，即n能整除a(xS-xR)。但是a与n互质，a与n的最大公因子是1，而xS-xR<n,因而左式不可能被n整除。也就是说这些数中的任意两个都不模n同余，φ(n)个数有φ(n)种余数。
(2)
这些数除n的余数都与n互质：
我们知道a，xi与n互质，则a × xi 与n互质，根据欧几里得算法，则n与（a × xi） %n也互质 。
那么这些数除n的余数，都在x1,x2,x3……xφ(n)中，因为这是1~n中与n互质的所有数，而余数又小于n.
由(1)和(2)可知，数m1,m2,m3……mφ(n)(如果将其次序重新排列)必须相应地同余于x1,x2,x3……xφ(n).
（解释）因为：m元素都在x元素的基础上乘了a，可能会造成元素互换，但实际上仍然是群里那phi（n）个元素而已
证明：只需证明mi != mj , mi=axi,mj=axj , 因为xi ！= xj ，所以mi != mj
故得出:m1*m2*m3……mφ(n)≡x1*x2*x3……xφ(n) (mod n)
或者说a^[φ(n)]*(x1*x2*x3……xφ(n))≡x1*x2*x3……xφ(n)
或者为了方便:K{a^[φ(n)]-1}≡0 ( mod n ) 这里K=x1*x2*x3……xφ(n)。
可知K{a^[φ(n)]-1}被n整除。但K中的因子x1,x2……都与n互质，所以K与n互质。那么a^[φ(n)]-1必须能被n整除，即a^[φ(n)]-1≡0 (mod n)，即a^[φ(n)]≡1 (mod n)，得证。
费马小定理: 只是取了p为质数的情况，使得容易得出φ(p)==p-1
a是不能被质数p整除的正整数，则有a^(p-1) ≡ 1 (mod p)
证明这个定理非常简单，由于p是质数，所以有φ(p) = p-1，代入欧拉定理即可证明。推论:对于任意正整数a，有a^p ≡ a (mod p)，因为a能被p整除时结论显然成立。
