仙人掌&圆方树
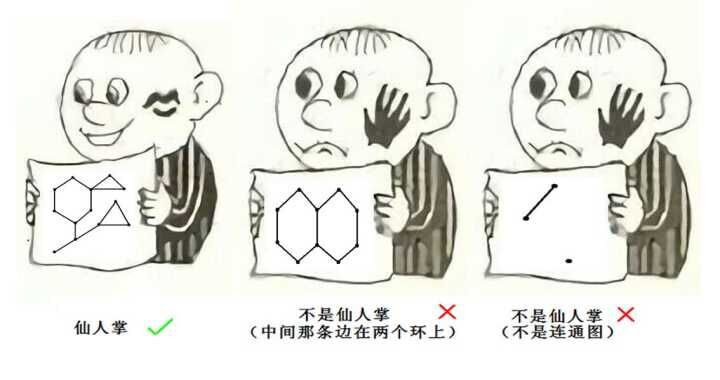
1. 仙人掌
无向连通图,每条边要么不在环里,要么只在一个环里。
2. 圆方树
仙人掌 \(G=(V,E)\) 的圆方树 \(T=(V_T,E_T)\) 为满足以下条件的无向图:
- \(V_T=R_T∪S_T\),\(R_T=V\),\(R_T∩S_T=∅\),其中 \(R_T\) 集合表示圆点,\(S_T\) 集合表示方点;
- \(∀e∈E\),若 \(e\) 不在任何简单环中,则 \(e∈E_T\);
- 对于每个仙人掌中的简单环 \(R\),存在方点 \(p_R∈S_T\),并且 \(∀p∈R\) 满足 \((p_R,p)∈E_T\),即对每个环建方点连所有点
简单来说,就是把所有环拆开,新建一个方点,连向所有环上点

代码:
void dfs(int x, int y) {
dfn[x] = ++tot;
fa[x] = y;
for (int i = head[x][0]; i; i = nxt[i]) {
if (to[i] == y) continue;
if (!dfn[to[i]]) {
mark[x] = 0;
dfs(to[i], x);
if (!mark[x]) add(x, to[i], 1);
} else {
if (dfn[to[i]] > dfn[x]) continue;
int u = x;
++num;
while (u != to[i]) {
add(num, u, 1);
u = fa[u];
mark[u] = 1;
}
add(to[i], num, 1);
}
}
}
3. 题
1. [BZOJ4316] 小 C 的独立集/洛谷U219357 xxqz 的独立集
做法:
考虑树的独立集,树形 dp,\(f[i][1/0]\) 表示节点 \(i\) 选/不选子树最大独立集,暴力转移。
变成仙人掌:圆点和圆点之间正常转移,遇到环直接把与根连接的两端拆开变成链,暴力 dp 把链两端的四种状态求出,再转移到根。
代码:
// Problem: U219357 xxqz 的独立集
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/U219357
// Memory Limit: 128 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
namespace Std {
int n, m, head[100010][2], nxt[400010], to[400010], cnt, dfn[100010],
fa[100010], tot, num, f[100010][2], g[100010][2];
bool mark[100010];
inline void add(int x, int y, bool z) {
to[++cnt] = y;
nxt[cnt] = head[x][z];
head[x][z] = cnt;
}
void dfs(int x, int y) {
dfn[x] = ++tot;
fa[x] = y;
for (int i = head[x][0]; i; i = nxt[i]) {
if (to[i] == y) continue;
if (!dfn[to[i]]) {
mark[x] = 0;
dfs(to[i], x);
if (!mark[x]) add(x, to[i], 1);
} else {
if (dfn[to[i]] > dfn[x]) continue;
int u = x;
++num;
while (u != to[i]) {
add(num, u, 1);
u = fa[u];
mark[u] = 1;
}
add(to[i], num, 1);
}
}
}
void dp(int x) {
f[x][1] = 1;
for (int i = head[x][1]; i; i = nxt[i]) {
if (to[i] <= n) {
dp(to[i]);
f[x][1] += f[to[i]][0];
f[x][0] += max(f[to[i]][1], f[to[i]][0]);
} else {
int u = to[i], f1, f2, f3, f4;
for (int j = head[u][1]; j; j = nxt[j]) dp(to[j]);
tot = 0;
g[0][0] = f[to[head[u][1]]][0];
g[0][1] = 0xc3c3c3c3;
for (int j = head[u][1]; j; j = nxt[j]) {
if (j == head[u][1]) continue;
++tot;
g[tot][1] = f[to[j]][1] + g[tot - 1][0];
g[tot][0] = f[to[j]][0] + max(g[tot - 1][0], g[tot - 1][1]);
}
f1 = g[tot][0];
f2 = g[tot][1];
g[0][0] = 0xc3c3c3c3;
g[0][1] = f[to[head[u][1]]][1];
tot = 0;
for (int j = head[u][1]; j; j = nxt[j]) {
if (j == head[u][1]) continue;
++tot;
g[tot][1] = f[to[j]][1] + g[tot - 1][0];
g[tot][0] = f[to[j]][0] + max(g[tot - 1][0], g[tot - 1][1]);
}
f3 = g[tot][0];
f4 = g[tot][1];
f[x][0] += max(max(f1, f2), max(f3, f4));
f[x][1] += f1;
}
}
}
int main() {
scanf("%d%d", &n, &m);
num = n;
int u, v;
for (int i = 1; i <= m; ++i) {
scanf("%d%d", &u, &v);
add(u, v, 0);
add(v, u, 0);
}
dfs(1, 0);
dp(1);
printf("%d\n", max(f[1][0], f[1][1]));
return 0;
}
} // namespace Std
int main() { return Std::main(); }
2. 洛谷P5236 【模板】静态仙人掌
做法:
树上做法:直接暴力 \(\text{LCA}\) 即可。
转化为仙人掌:先建出圆方树,然后对于 \(\text{LCA}\) 是圆点的情况和树的一样,如果 \(\text{LCA}\) 是方点,重新把每个点跳到所属环,求一下两点的换上距离即可。
代码:
// Problem: P5236 【模板】静态仙人掌
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5236
// Memory Limit: 125 MB
// Time Limit: 300 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
namespace Std {
int n, m, head[20010][2], nxt[80010], to[80010], cnt, dfn[20010], fa[20010],
tot, num, len[80010], q, dep[20010], d[20010][20], f[20010][20], top[20010],
lenh[20010], dis[20010];
bool mark[20010];
inline void add(int x, int y, int z, bool t) {
to[++cnt] = y;
len[cnt] = z;
nxt[cnt] = head[x][t];
head[x][t] = cnt;
}
void dfs(int x, int y) {
dfn[x] = ++tot;
fa[x] = f[x][0] = y;
for (int i = head[x][0]; i; i = nxt[i]) {
if (to[i] == y) continue;
if (!dfn[to[i]]) {
mark[x] = 0;
dis[to[i]] = dis[x] + len[i];
d[to[i]][0] = len[i];
dfs(to[i], x);
if (!mark[x]) add(x, to[i], len[i], 1);
} else {
if (dfn[to[i]] > dfn[x]) continue;
int u = x;
++num;
lenh[num] = dis[x] - dis[to[i]] + len[i];
while (u != to[i]) {
f[u][0] = num;
d[u][0] = min(dis[u] - dis[to[i]], lenh[num] - dis[u] + dis[to[i]]);
add(num, u, d[u][0], 1);
u = fa[u];
mark[u] = 1;
}
f[num][0] = to[i];
d[num][0] = 0;
add(to[i], num, 0, 1);
}
}
}
void dfs2(int x) {
for (int i = head[x][1]; i; i = nxt[i]) {
dep[to[i]] = dep[x] + 1;
dfs2(to[i]);
}
}
void init(void) {
for (int i = 1; i < 20; ++i) {
for (int j = 1; j <= num; ++j) {
f[j][i] = f[f[j][i - 1]][i - 1];
d[j][i] = d[j][i - 1] + d[f[j][i - 1]][i - 1];
}
}
}
int query(int x, int y) {
int u = x, v = y, ans = 0;
if (dep[u] < dep[v]) swap(u, v);
for (int i = 19; ~i; --i) {
if (dep[f[u][i]] < dep[v]) continue;
ans += d[u][i];
u = f[u][i];
}
if (u != v) {
for (int i = 19; ~i; --i) {
if (f[u][i] == f[v][i]) continue;
ans += d[u][i] + d[v][i];
u = f[u][i], v = f[v][i];
}
if (u != v) {
if (dep[u] == dep[v]) {
ans += d[u][0] + d[v][0];
u = f[u][0], v = f[v][0];
} else {
if (dep[u] > dep[v]) {
ans += d[u][0];
u = f[u][0];
} else {
ans += d[v][0];
v = f[v][0];
}
}
}
}
if (u > n) {
ans = 0;
for (int i = 19; ~i; --i) {
if (dep[f[x][i]] > dep[u]) {
ans += d[x][i];
x = f[x][i];
}
if (dep[f[y][i]] > dep[u]) {
ans += d[y][i];
y = f[y][i];
}
}
ans += min(abs(dis[x] - dis[y]), lenh[u] - abs(dis[x] - dis[y]));
}
return ans;
}
int main() {
scanf("%d%d%d", &n, &m, &q);
num = n;
int u, v, w;
for (int i = 1; i <= m; ++i) {
scanf("%d%d%d", &u, &v, &w);
add(u, v, w, 0);
add(v, u, w, 0);
}
dep[1] = 1;
dfs(1, 0);
dfs2(1);
init();
for (int i = 1; i <= q; ++i) {
scanf("%d%d", &u, &v);
printf("%d\n", query(u, v));
}
return 0;
}
} // namespace Std
int main() { return Std::main(); }
3. P4244 [SHOI2008]仙人掌图 II
做法:
树上做法有两种,一种是两遍 \(\text{dfs}\) 的做法,一种是 \(\text{dp}\) 做法,两种方法都很简单。
换成仙人掌:贪心做法换到仙人掌上来做并不容易,考虑 \(\text{dp}\)。设 \(f[i][0/1]\) 表示节点 \(i\) 为一端子树内最长/次长链长度,圆点转移很简单,遇到环,直接环形 \(\text{dp}\),求出环对总答案的贡献,再利用环上点到环的根节点距离求出根节点的 \(f[i][0/1]\)。
代码:
// Problem: P4244 [SHOI2008]仙人掌图 II
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4244
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
#define add(x, y, z) to[x][z].push_back(y)
using namespace std;
namespace Std {
inline bool maxy(int &x, int y) { return (x = max(x, y)); }
int n, m, num, stack[100010], top, fa[100010], dfn[100010], tot, f[100010][2],
len[100010], q1[100010], q2[100010], ans;
vector<int> to[100010][2];
bool mark[100010];
void dfs1(int x) {
dfn[x] = ++tot;
for (auto i : to[x][0]) {
if (i == fa[x]) continue;
if (!dfn[i]) {
mark[x] = false;
fa[i] = x;
dfs1(i);
if (!mark[x]) add(x, i, 1);
} else {
if (dfn[i] > dfn[x]) continue;
++num;
add(i, num, 1);
int u = x;
while (u != i) {
add(num, u, 1);
u = fa[u];
mark[u] = true;
}
}
}
}
void dfs2(int x) {
for (auto i : to[x][1]) {
if (i <= n) {
dfs2(i);
if (f[i][0] + 1 >= f[x][0]) {
if (f[x][0] >= f[x][1]) {
f[x][1] = f[x][0];
}
f[x][0] = f[i][0] + 1;
} else if (f[i][0] + 1 >= f[x][1])
f[x][1] = f[i][0] + 1;
} else {
int u = i;
for (auto j : to[u][1]) {
dfs2(j);
}
top = 0;
for (auto j : to[u][1]) {
stack[++top] = j;
}
stack[++top] = x;
int l1 = 1, r1 = 0, l2 = 1, r2 = 0;
for (int j = 1; j <= (top >> 1); ++j) {
while (l1 <= r1 && j + f[stack[j]][0] > q1[r1] + f[stack[q1[r1]]][0])
--r1;
q1[++r1] = j;
}
for (int j = (top >> 1) + 1; j < top; ++j) {
while (l2 <= r2 && f[stack[j]][0] - j > f[stack[q2[r2]]][0] - q2[r2])
--r2;
q2[++r2] = j;
}
for (int j = 1; j < top - 1; ++j) {
if (j + (top >> 1) < top) {
if (q2[l2] == j + (top >> 1)) ++l2;
while (l1 <= r1 && j + (top >> 1) + f[stack[j + (top >> 1)]][0] >
q1[r1] + f[stack[q1[r1]]][0])
--r1;
q1[++r1] = j + (top >> 1);
}
if (q1[l1] == j) ++l1;
if (l2 <= r2)
maxy(ans,
max(q1[l1] + f[stack[q1[l1]]][0] + f[stack[j]][0] - j,
f[stack[j]][0] + j + top - q2[l2] + f[stack[q2[l2]]][0]));
else
maxy(ans, q1[l1] + f[stack[q1[l1]]][0] + f[stack[j]][0] - j);
}
int maxn = 0;
for (int j = 1; j < top; ++j) {
maxn = max(maxn, f[stack[j]][0] + min(j, top - j));
}
if (maxn >= f[x][0]) {
if (f[x][0] >= f[x][1]) {
f[x][1] = f[x][0];
}
f[x][0] = maxn;
} else if (maxn >= f[x][1])
f[x][1] = maxn;
}
}
maxy(ans, f[x][1] + f[x][0]);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int t, u, v;
scanf("%d", &t);
if (t) scanf("%d", &u);
for (int j = 1; j < t; ++j) {
scanf("%d", &v);
add(u, v, 0);
add(v, u, 0);
u = v;
}
}
num = n;
dfs1(1);
dfs2(1);
printf("%d\n", ans);
return 0;
}
} // namespace Std
int main() { return Std::main(); }
4. P3180 [HAOI2016]地图
做法:
考虑树的做法,线段树合并板子题,直接暴力合并即可。
变成仙人掌,我们发现,环上的点分为两类,与全图根节点最近的一个点是一类,其余点是另一类,对于第一类点,环上其余所有点都可以视为其子树范围内,对于第二类点,环上其余所有点都不包含在其子树范畴。所以原图可以转化为第一类点向第二类点连边,这样就变成了树的问题。
代码:
// Problem: P3180 [HAOI2016]地图
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3180
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
#define add(x, y, z) to[x][z].push_back(y)
using namespace std;
namespace Std {
int n, m, cnt, dfn[100010], fa[100010], tot, q, num[100010], po[100010],
type[100010], li[100010], ans[100010];
bool mark[100010];
vector<int> vec[100010], to[100010][2];
struct tree {
tree *ls, *rs;
int num1, num2;
tree() {
ls = rs = NULL;
num1 = num2 = 0;
}
void pushup() {
if (ls == NULL) {
num1 = rs->num1;
num2 = rs->num2;
} else if (rs == NULL) {
num1 = ls->num1;
num2 = ls->num2;
} else {
num1 = ls->num1 + rs->num1;
num2 = ls->num2 + rs->num2;
}
}
void change(int l, int r, int pos) {
if (l == r) {
if ((!num1 && (!num2))) num2 = 1;
if (num1)
num1 = 0, num2 = 1;
else
num2 = 0, num1 = 1;
return;
}
int mid = ((l + r) >> 1);
if (pos <= mid) {
if (ls == NULL) ls = new tree;
ls->change(l, mid, pos);
} else {
if (rs == NULL) rs = new tree;
rs->change(mid + 1, r, pos);
}
pushup();
}
void merge(tree *x, int l, int r) {
if (l == r) {
if (x->num1) {
if (num1)
num1 = 0, num2 = 1;
else
num1 = 1, num2 = 0;
}
return;
}
int mid = (l + r) >> 1;
if (ls != NULL && x->ls != NULL)
ls->merge(x->ls, l, mid);
else if (x->ls != NULL)
ls = x->ls;
if (rs != NULL && x->rs != NULL)
rs->merge(x->rs, mid + 1, r);
else if (x->rs != NULL)
rs = x->rs;
pushup();
}
int query(int l, int r, int L, int R, int opt) {
if (L <= l && r <= R) return opt ? num1 : num2;
int tmp = 0;
int mid = (l + r) >> 1;
if (L <= mid && ls != NULL) tmp += ls->query(l, mid, L, R, opt);
if (R > mid && rs != NULL) tmp += rs->query(mid + 1, r, L, R, opt);
return tmp;
}
} * rt[100010];
void dfs(int x, int y) {
dfn[x] = ++tot;
fa[x] = y;
for (auto i : to[x][0]) {
if (i == y) continue;
if (!dfn[i]) {
mark[x] = 0;
dfs(i, x);
if (!mark[x]) add(x, i, 1);
} else {
if (dfn[i] > dfn[x]) continue;
int u = x;
while (u != i) {
add(i, u, 1);
u = fa[u];
mark[u] = 1;
}
}
}
}
void dfs2(int x) {
rt[x] = new tree;
rt[x]->change(1, 1000000, num[x]);
for (auto i : to[x][1]) {
dfs2(i);
rt[x]->merge(rt[i], 1, 1000000);
}
for (auto i : vec[x]) {
ans[i] = rt[x]->query(1, 1000000, 1, li[i], type[i]);
}
}
int main() {
scanf("%d%d", &n, &m);
int u, v;
for (int i = 1; i <= n; ++i) {
scanf("%d", num + i);
}
for (int i = 1; i <= m; ++i) {
scanf("%d%d", &u, &v);
add(u, v, 0);
add(v, u, 0);
}
dfs(1, 0);
scanf("%d", &q);
for (int i = 1; i <= q; ++i) {
scanf("%d%d%d", type + i, po + i, li + i);
vec[po[i]].push_back(i);
}
dfs2(1);
for (int i = 1; i <= q; ++i) printf("%d\n", ans[i]);
return 0;
}
} // namespace Std
int main() { return Std::main(); }
未经授权,禁止转载。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号