时间序列分析2.X AR与MA
ARMA与ARIMA模型
对平稳时间序列和非平稳时间序列,分别假定适当的 ARMA 模型和 ARIMA 模型
对非平稳时间序列建立 ARIMA 模型,实际上是通过先用适当的变换将非平稳序列转化为平稳序列,然后再建立 ARMA 模型
差分消除趋势性和季节性
将非平稳序列化为平稳序列的常见变换
- 趋势差分以消除趋势性
- 季节差分以消除季节性
- Box-Cox 变换以使得波动稳定化
趋势差分
季节差分
s 常取12
当序列同时有趋势性与周期性时,先趋势差分,再季节差分
对于波动随时间变化的序列变为平稳序列
- 先做适当的 Box-Cox 变换,使得其波动稳定化,然后再进行差分运算消除趋势性和季节性
- 先取对数,再趋势差分,最后季节差分
平稳过程
弱平稳过程
定义
满足:
为常数 与 无关,
即称为弱平稳过程
性质
(波动不会随时间变化) 只与 有关 两点相关性只与间隔有关.(由此可以用昨天到今天的规律,根据今天的情况预测明天)
白噪声过程
满足:
- 不必相互独立
称为白噪声过程,
性质
- 满足
,即无序列相关性
随机漫步(RW)
随机漫步
定义
如果
经过地推可以得到
性质
假设
, 对于随机漫步而言, 与
有关, 故不是平稳过程
带漂移项的随机漫步
定义
如果
经过推导可得
性质
假设
, 对于带漂移项的随机漫步而言, 与
有关, 故不是平稳过程
ACF 及序列相关性的度量
ACF
延迟 k 自协方差函数
延迟 k 自相关函数
常记作
ACF性质
样本自相关函数
间隔 k 的相关系数
自相关图
以延迟阶数
为横坐标, 为纵坐标绘图
AR自回归模型
满足
的平稳的 称为
(中心化的)阶自回归过程, 记为
一般的
可以表示为
其可以等价展开成,
其中
模型样式
性质
由于
与 有相同的方差与协方差, 故我们可以令
容易验证,当时,
对模型重复进行迭代, 我们有
一直进行下去,如果
容易验证其为平稳序列, 且其ACF函数为 Xt 可以表示为当前和过去时刻扰动的收敛线性组合,即
形式,此时称 Xt 是因果过程。我们也可以得出结论: 是因果平稳的充要条件是
期望与ACF
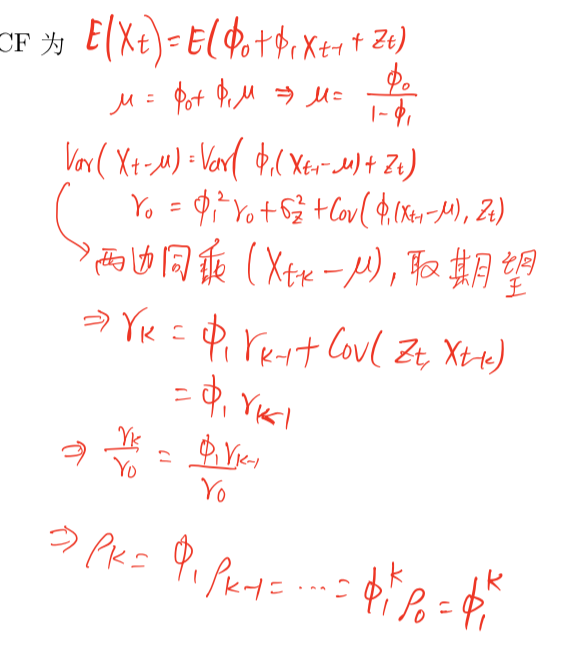
模型表示
因果平稳条件
, 为 的两个根的倒数
令
, 有
当, 为因果平稳过程
当, 可表示为
也为因果平稳过程
所以, AR(2) 为因果平稳过程的条件是
的两个根在单位圆外, 即 ,
ACF
(为方便研究, 无妨设 )
两边同时乘以
并取期望
有
再两边同除以
, 可得到
令
, 利用 , 有
由
, 与 ,可以计算任意阶延迟的ACF
平均周期长度
特征方程为
若特征方程的根为共轭复特征根
记为
则平均周期长度
AR建模
步骤
- 确保对象为平稳序列
- 定阶
- 估计参数
- 残差诊断
- 优化
- 预测
定阶
PACF定阶
定义
通过PACF图在处截尾, 选取
信息准则定阶
- 赤池信息准则 (AIC)
- 贝叶斯信息准则 (BIC)
MA移动平均模型
满足
的平稳过程
性质
平稳性
不需要系数满足额外的限制条件,
模型总是因果平稳的
以及
均与 无关;
ACF
这里记
。
于是,
过程的 为
可逆性
定义
如果
时刻的随机扰动可以表示为当前值和历史值的一个收敛和的形式,即
其中,
.
形式
MA建模
定阶
通过ACF图在
处截尾, 选取





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通