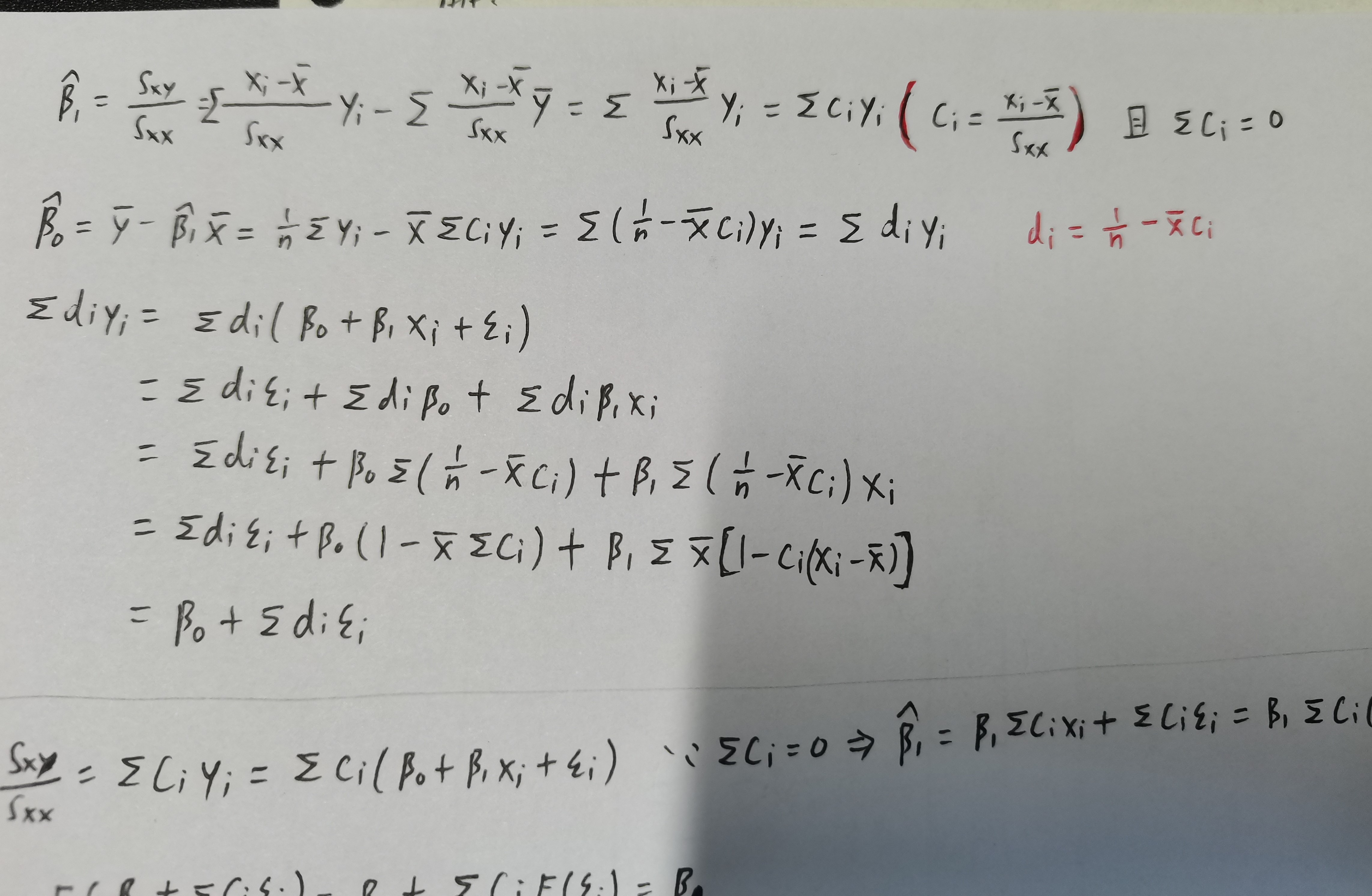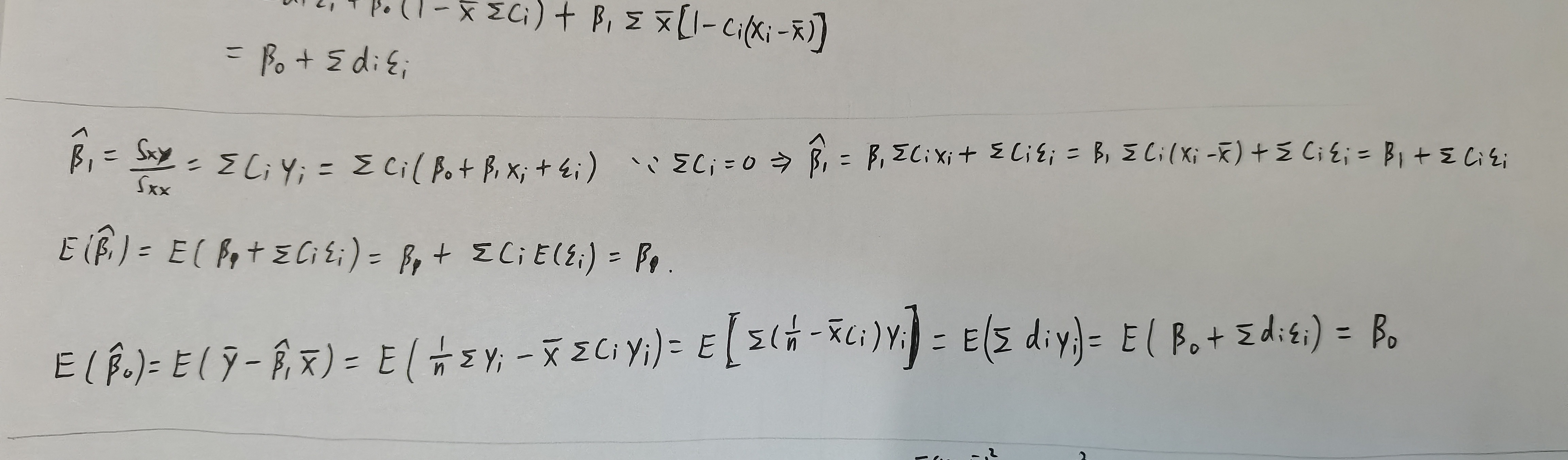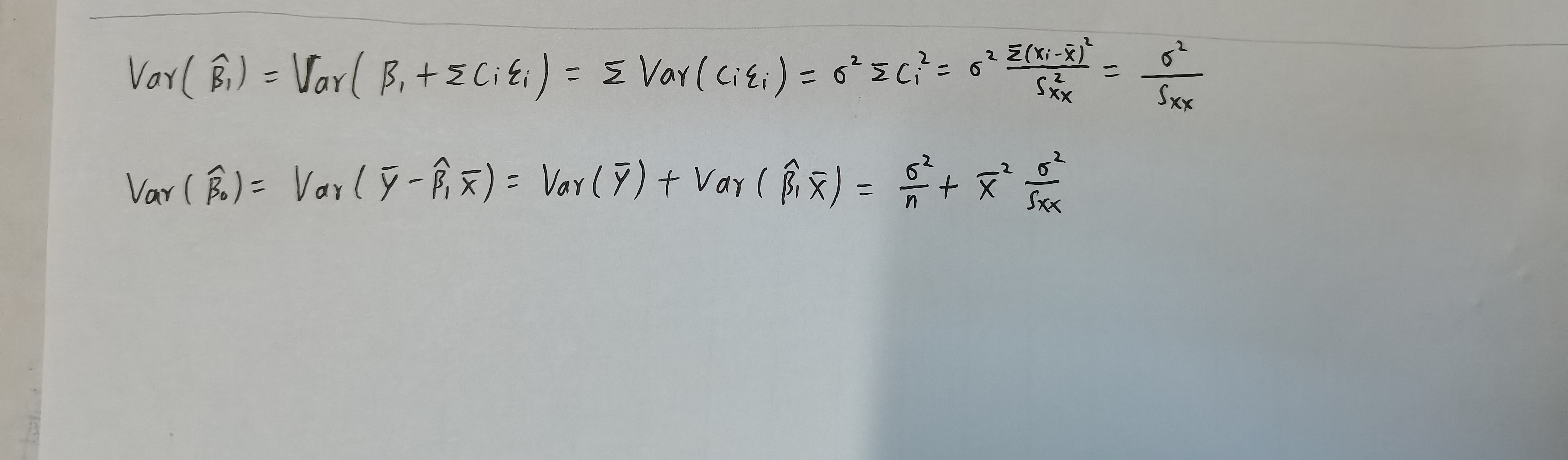回归分析-2.X 简单线性回归
2.1
简单线性回归模型
y与x之间的关系假设
\(y=\beta_0+\beta_1x+\varepsilon\)
\(E(\varepsilon|x)=0\)
\(Var(\varepsilon|x)=\sigma^2~则~Var(y|x)=\sigma^2\) 同方差假定
2.2
回归参数的最小二乘估计
回归系数 \(\beta_0,~\beta_1\) 的估计
残差平方和
\[S(\hat{\beta}_0,\hat{\beta}_1)=\sum^n_{i=1}(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)^2 \]
分别求偏导得到
\[\hat{\beta}_{0}=\bar{y}-\hat{\beta}_{1} \bar{x} \]\[\hat{\beta}_{1}=\frac{\sum_{i=1}^{n} x_{i} y_{i}-n \cdot \bar{x} \cdot \bar{y}}{\sum_{i=1}^{n} x_{i}^{2}-n \cdot \bar{x}^{2}}=\frac{\sum\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sum\left(x_{i}-\bar{x}\right)^{2}}=\frac{S_{x y}}{S_{x x}} \]
性质
\[\frac{\partial S}{\partial\beta_0}=\sum(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)=0~\Rightarrow~\sum e_i=0 \]
\[\frac{\partial S}{\partial\beta_1}=\sum(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)x_i=0~\Rightarrow \]\[\sum e_ix_i=\sum (e_i-\bar{e})x_i=\sum(e_i-\bar{e})(x_i-\bar{x})=0 \]进而知道\(\{e_i\}与\{x_i\}\) 互不相关
\(\sum(e_i-\bar{e})(y_i-\bar{y})=\sum e_iy_i=\sum e_i(\hat{\beta}_0+\hat{\beta}_1x_i)=\hat{\beta}_0\sum e_i+\hat{\beta}_1\sum(e_ix_i)=0\)
因此得出\(\{e_i\}与\{y_i\}\) 互不相关
\(\{e_i\}与\{\hat{y}_i\}\) 互不相关
\(Cov(\bar{y},\hat{\beta}_1)=0\)
\[\begin{aligned} Cov(\bar{y},\hat{\beta}_1)&=\frac{1}{n}\sum Cov(y_i,\hat{\beta}_1)\\ &=\frac{1}{n}Cov(\sum y_i,\sum c_iy_i)\\ &=\frac{1}{n}\sum (c_i\sigma^2)\\ &=0 \end{aligned}\]
- OLS是线性估计
- OLS是无偏估计
- LS估计的方差可计算为
随机误差方差的 \(\sigma^2\) 估计
均方误差
\[\begin{array} aMSE(\theta)=E(\hat{\theta}-\theta)^2=E(\hat{\theta}-E(\hat{\theta})+E(\hat{\theta})-\theta)^2=Var(\hat{\theta})+(bias(\hat{\theta}))^2\\ bias(\hat{\theta})=E(\hat{\theta})-\theta\end{array}\]
定义
\[S S_{\text {Res }}=\sum_{i=1}^{n} e_{i}^{2}=\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}=\sum_{i=1}^{n}\left(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1} x_{i}\right)^{2} \]\[\hat{\sigma}^{2}=\frac{S S_{\text {Res }}}{n-2}=M S_{\text {Res }} \]
在第三章我们将证明 \(E\left(\hat{\sigma}^{2}\right)=\sigma^{2}\)
参数估计的标准误
\[s.e.(\hat{\beta}_1)=\sqrt{\frac{\frac{S S_{\text {res }}}{n-2}}{S_{xx}}} \]\[s.e.(\hat{\beta}_0)=\sqrt{\frac{\frac{S S_{\text {res }}}{n-2}}{n}+\bar{x}^2\frac{\frac{S S_{\text {res }}}{n-2}}{S_{xx}}} \]
2.3
斜率与截距的假设检验
OLS 估计的抽样分布
\[\hat{\beta}_{1}=\sum_{i=1}^{n} c_{i} y_{i}=\beta_{1}+\sum_{i=1}^{n} c_{i} \epsilon_{i}, \quad \hat{\beta}_{0}=\sum_{i=1}^{n} d_{i} y_{i}=\beta_{0}+\sum_{i=1}^{n} d_{i} \epsilon_{i} \]\[\hat{\beta}_{1}\sim N(\beta_1,\frac{\sigma^2}{S_{xx}})~,~ ~ \hat{\beta}_{0}\sim N(\beta_0,\bar{x}^2\frac{\sigma^2}{S_{xx}}) \]
t 检验
由于
\[t_{0}=\frac{\hat{\beta}_{1}-\beta_{10}}{\hat{\sigma} / \sqrt{S_{x x}}}=\frac{\hat{\beta}_{1}-\beta_{10}}{\hat{\sigma} / \sqrt{S_{x x}}} \frac{\sigma}{\hat{\sigma}}=\frac{Z_{0}}{\sqrt{\frac{SS_{\text {res }}}{(n-2) \sigma^{2}}}}=Z_{0} / \sqrt{\frac{M S_{\text {res }}}{\sigma^{2}}} \sim t(n-2) \]因此,为了检验两变量间是否有线性关系,将假设斜率 \(\beta_{10}=0\)
t检验统计量为
\[t=\frac{\hat{\beta}_1}{\hat{\sigma}/\sqrt{S_{xx}}}=\frac{\hat{\beta}_1}{s.e.(\hat{\beta}_1)}={\hat{\beta}_1}/{\sqrt{\frac{\frac{S S_{\text {res }}}{n-2}}{S_{xx}}}} \]
p 值
\[pvalue=P(|t_{n-2}|>|\frac{\hat{\beta}_1}{s.e.(\hat{\beta}_1)}|) \]
区间估计
参数的置信区间
\(\beta_0~\beta_1\)的置信区间
\[\frac{\hat{\beta}_{1}-\beta_{1}}{s . e .\left(\hat{\beta}_{1}\right)} \sim t({n-2}), \quad \frac{\hat{\beta}_{0}-\beta_{0}}{s . e .\left(\hat{\beta}_{0}\right)} \sim t({n-2}) \]可得 \(\beta_{i}\) 的 \(1-\alpha\) 置信区间为
\[\hat{\beta}_{i} \pm t_{n-2}(1-\alpha / 2) * \text { s.e. }\left(\hat{\beta}_{i}\right) \]
响应变量均值 \(E(y|x_0)\) 的估计和置信区间
\(\because\)
\(E\left(y \mid x_{0}\right)=\beta_{0}+\beta_{1} x_{0}\)
\(\therefore\)
\(\hat{\mu}_{y \mid x_{0}}=\hat{\beta}_{0}+\hat{\beta}_{1} x_{0}=\bar{y}+\hat{\beta}_{1}\left(x_{0}-\bar{x}\right)\)
而且
\[Var\left(y \mid x_{0}\right)=\sigma^2({\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}}}) \]
可知
\[\frac{\hat{\mu}_{y \mid x_{0}}-\mu_{y \mid x_{0}}}{\hat{\sigma} \sqrt{\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}}}} \sim t({n-2}) \]
所以\(E(y|x_0)\) 的置信区间
\[\hat{\mu}_{y \mid x_{0}}\pm t_{n-2}(1-\alpha/2)\hat{\sigma} \sqrt{\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}}} \]
新观测的预测
预测误差为
\[\begin{aligned}\psi&=y_{0}-\hat{y}_{0}\\ &=\beta_{0}+\beta_{1} x_{0}+\epsilon_{0}-(\hat{\beta}_{0}+\hat{\beta}_{1} x_{0})\\ &=(\beta_{0}-\hat{\beta}_{0})+(\beta_{1}-\hat{\beta}_{1}) x_{0}+\epsilon_{0} \end{aligned}\]
预测方差为
\[\begin{aligned}\operatorname{Var}(\psi)&=\operatorname{Var}(y_{0}-\hat{y}_{0})\\ &=\operatorname{Var}(\hat{\beta}_{0}+\hat{\beta}_{1} x_{0}+\epsilon_{0})\\ &=\sigma^2(1+\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}}) \end{aligned}\]
因此有
\[\frac{\psi-E(\psi)}{\sqrt{\operatorname{Var}(\psi)}}=\frac{y_{0}-\hat{y}_{0}}{\sigma \sqrt{1+\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}}}} \sim N(0,1) \]
所以
\[\frac{y_{0}-\hat{y}_{0}}{\hat{\sigma} \sqrt{1+\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}}}} \sim t_{n-2} \]
于是可得 \(1-\alpha\) 预测区间为
\[\hat{y}_{0} \pm t_{n-2}(1-\alpha / 2) \hat{\sigma} \sqrt{1+\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{S_{x x}}} \]
决定系数 \(R^2\)
可以定义
\[\begin{aligned} S S_{\text {total }}&=\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}\\ &=\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}+\hat{y}_{i}-\bar{y}\right)^{2}\\ &=\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}+\sum_{i=1}^{n}\left(\hat{y}_{i}-\bar{y}\right)^{2}+2 \sum_{i=1}^{n} e_{i}\left(\hat{y}_{i}-\bar{y}\right) \triangleq \text { SSres }+\text { SSreg } \end{aligned}\]
\[R^{2}=\frac{SS_{reg}}{SS_T}=\frac{S S_{t o t a l}-S S_{r e s}}{S S_{t o t a l}} \]表明了 y 的样本变异中被 x 解释了的部分
可以推导出下列结论
\[R^{2}=\frac{\hat{\beta}_{1}^{2}}{\hat{\beta}_{1}^{2}+\frac{n-2}{n-1} \cdot \frac{\hat{\sigma}^{2}}{\hat{\sigma}_{x}^{2}}} \]因此 \(R^{2}\) 较大, 并不意味着斜率 \(\hat{\beta}_{1}\) 就较大;
- 应该谨慎地解释和使用 \(R^{2}\) 。在实际问题里, \(R^{2}\) 作为模型拟合优 度的度量是有缺陷的, 一个典型的问题是, 在多元线性回归模型 里, 加人一个变量总会使得 \(R^{2}\) 升高, 因此用它做标准选择模型 的话, 总是会选取一个最复杂的模型。
- 若 \(R^{2}=1\) ,则完美拟合
- 若 \(R^{2}=0\) ,则两变量无关系