给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
示例:
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
说明:
假设你总是可以到达数组的最后一个位置。
链接:https://leetcode-cn.com/problems/jump-game-ii
思路1:超内存的动态规划:
class Solution { public int jump(int[] nums) { if(nums.length==25000) { return 24999; } if(nums[0]==25000) { return 2; } int [][] dp =new int[nums.length][nums.length]; // System.out.print(nums.length); // for(int i=0;i<dp.length;i++){ //0,1,2 // for(int j=0;j<dp[i].length;j++){ //每一个一维数组的长度 // dp[i][j]=nums.length+1; // // System.out.print(dp[i][j]+"\t"); // } // // System.out.println(); // } // //对角线全部为0 // for(int ii=0;ii<nums.length;ii++) // { // dp[ii][ii]=0; // } for(int i=nums.length-2;i>=0 ;i--) { // System.out.println("i="+i); if(nums[i]==0) { for(int j=i;j<nums.length;j++) { dp[i][j]=nums.length+1;//如果当前的数值为0 将步数到最大 // System.out.println("dp[i][j] 无穷的情况"+i+" "+j+" "+dp[i][j]); } continue; } for(int j=i+1;j<nums.length;j++) { dp[i][j]=nums.length+1; if(j<=(i+nums[i])) {//如果当前要去的点 我直接能跳到那个地方 置为1 直接下一步 dp[i][j]=1; // continue; // System.out.println("dp[i][j]==1的情况"+i+" "+j+" "+dp[i][j]); } else {//如果不能一次跳到 for(int k=i+1;k<=i+nums[i];k++) {//去找 1+dp[所有能跳到的点][nums.length-1] 中最小的 int temp_min=1+dp[k][nums.length-1]; if(dp[i][j]>temp_min) { dp[i][j]=temp_min; } } // System.out.println("dp[i][j]!=1的情况"+i+" "+j+" "+dp[i][j]); } } } return dp[0][nums.length-1]; } }
思路2 :一维的dp
class Solution { public: int jump(vector<int>& nums) { int n = nums.size(); vector<int> f(n, 0x3f3f3f3f); for (int i = 0; i < n; i++) { if (!i) f[i] = 0; // 处理边界 else { for (int j = 0; j < i; j++) { if (j + nums[j] >= i) { // 只要前面的点能跳到i点就更新最小值 f[i] = min(f[i], f[j] + 1); } } } } return f[n - 1]; } };
class Solution { public int jump(int[] nums) { int[] dp = new int[nums.length]; for(int i = 0 ; i < nums.length; ++ i) { dp[i] = 0x3f3f3f3f; } dp[0]= 0; for(int i = 0; i < nums.length; ++ i) { int max = Math.min(nums.length -1,nums[i]+i); for(int j = i ; j<= max;++ j) { dp[j] = Math.min(dp[j], dp[i] + 1); } } return dp[nums.length - 1]; } }
贪心:
解法一 :顺藤摸瓜
LeetCode 讨论里,大部分都是这个思路,贪婪算法,我们每次在可跳范围内选择可以使得跳的更远的位置。
如下图,开始的位置是 2,可跳的范围是橙色的。然后因为 3 可以跳的更远,所以跳到 3 的位置。
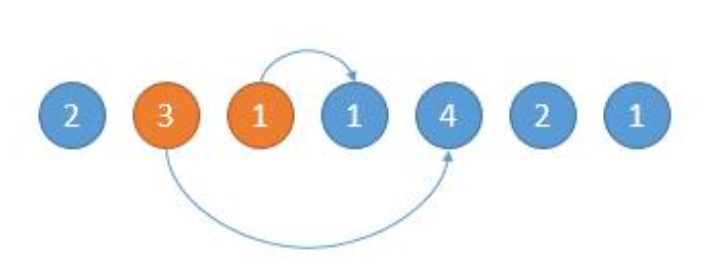
如下图,然后现在的位置就是 3 了,能跳的范围是橙色的,然后因为 4 可以跳的更远,所以下次跳到 4 的位置。
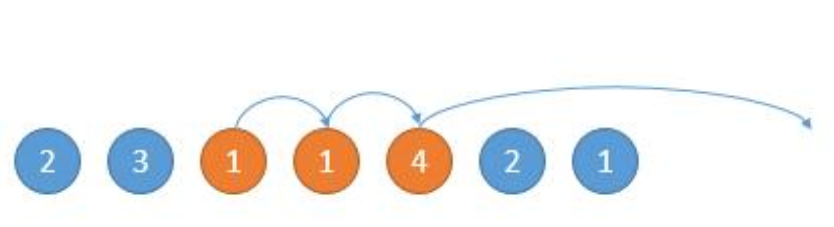
写代码的话,我们用 end 表示当前能跳的边界,对于上边第一个图的橙色 1,第二个图中就是橙色的 4,遍历数组的时候,到了边界,我们就重新更新新的边界。
Java
public int jump(int[] nums) { int end = 0; int maxPosition = 0; int steps = 0; for(int i = 0; i < nums.length - 1; i++){ //找能跳的最远的 maxPosition = Math.max(maxPosition, nums[i] + i); if( i == end){ //遇到边界,就更新边界,并且步数加一 end = maxPosition; steps++; } } return steps; }



