CF1041F Ray in the tube 题解

\(1.\) 题意

给定两条数轴，上轴有 \(n\) 个关键点，下轴有 \(m\) 个关键点。要求在下轴寻找 \(A\) 点和在上轴寻找 \(B\) 点，使从 \(A\) 向 \(B\) 发射光线在两个轴之间反射（碰到轴即反射，每个反射点必须是整点，满足反射定律）可以经过的关键点最多，输出最大值。

\(2.\) 思路

首先明确给的纵坐标没有任何用。光线经过的点只由 \(A,B\) 两点决定。

设 \(A,B\) 的横坐标差的绝对值为 \(L\)。然后我们通过画图发现对于一个 \(L\)，若 \(L\) 包含一个大于 \(1\) 的奇数因子 \(k\)，那么这个 \(L\) 一定不如 \(L \over k\) 优。 如图，同一点 \(L\) 形成的光线在包含 \(3L\) 光线所经过点的基础上还多包含了紫色的点。所以 \(L\) 严格优于 \(3L\)。

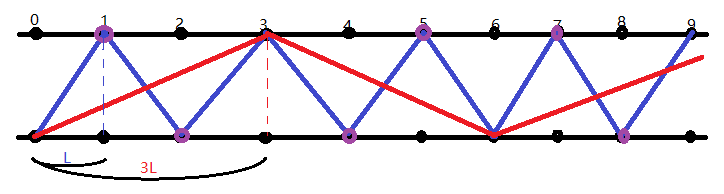
于是我们发现对于一个固定点的 \(L\) 只能取 \(2\) 的整数次幂。\(L = 2^n\)，所以 \(L\) 一共有 \(\log_210^9\) 个取值不到 \(30\) 个，所以对于固定位置直接枚举。

观察发现，对于下方的关键点满足横坐标为 \(L\) 的偶数倍时可以被选到，上方的关键点满足横坐标为 \(L\) 的奇数倍时可以被选到。开一个 \(map\) 扫描每一个关键点，对于每一个 \(L\) 的可能取值，使其在模 \(2L\) 的意义下的起点加一，最后取最大值。复杂度 \(O(N\log N \log_2 10^9)\)

\(3.\) 代码

const int N = 2e5 + 10;
int a[N], b[N], n, m, nouse, ans;
map<int, int> M;

inline void check(int x){
    M.clear();
    for(int i = 1; i <= n; i ++) M[a[i] % (x << 1)] ++;
    for(int i = 1; i <= m; i ++) M[(b[i] + x) % (x << 1)] ++;
    for(auto v : M) ans = max(ans, v.second);
}

signed main(){
    read(n), read(nouse); for(int i = 1; i <= n; i ++) read(a[i]);
    read(m), read(nouse); for(int i = 1; i <= m; i ++) read(b[i]);
    for(int i = 1; i <= n; i ++) M[a[i]] ++;
    for(int i = 1; i <= m; i ++) M[b[i]] ++;
    for(auto v : M) ans = max(ans, v.second);
    for(int i = 0; i <= 29; i ++) check(1 << i);
    print(ans); return 0;
}