后缀自动机入门及例题
后缀自动机
一、SAM的性质
-
SAM是个状态机。一个起点,若干终点。原串的所有子串和从SAM起点开始的所有路径一一对应,不重不漏。所以终点就是包含后缀的点。
-
每个点包含若干子串,每个子串都一一对应一条从起点到该点的路径。且这些子串一定是里面最长子串的连续后缀。
-
SAM问题中经常考虑两种边:
(1)普通边,类似于 。表示在某个状态所表示的所有子串的后面添加一个字符。
(2) 表示将某个状态所表示的最短子串的首字母删除。这类边构成一棵树。
二、SAM的构造思路
-
:子串 所有出现的位置(尾字母下标)集合。SAM中的每个状态都一一对应一个 的等价类。
endpos的性质: -
(1) 令 为 的两个子串 ,不妨设 。则 是 的后缀当且仅当 , 不是 的后缀当且仅当 ∩ ∅ 。
(2) 两个不同子串的 ,要么有包含关系,要么没有交集。
(3) 两个子串的 相同,那么短串为长串的后缀。
(4) 对于一个状态 ,以及任意的 的后缀 ,如果 的长度满足: ,那么 。
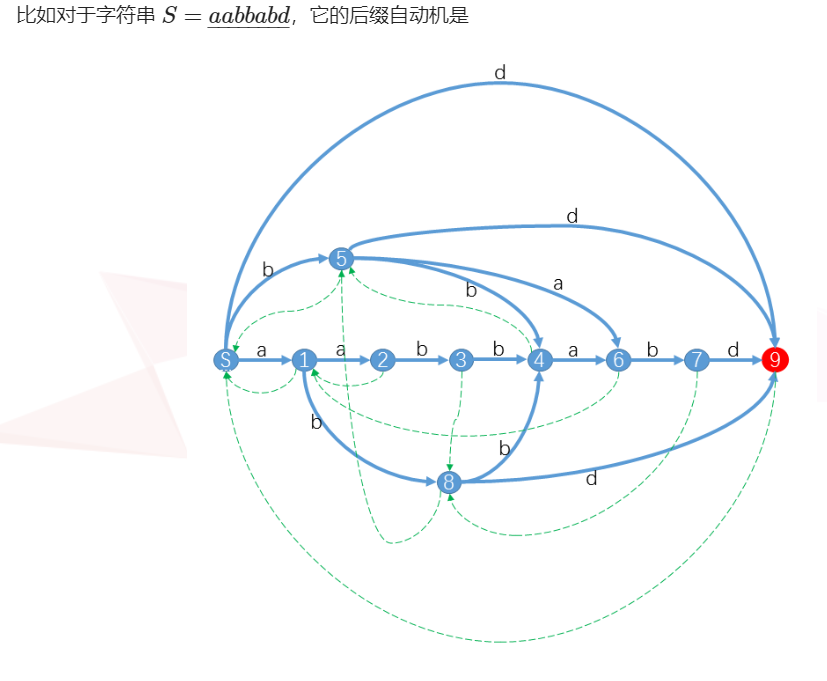
例题:
模板后缀自动机
#include <map>
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#define ll long long
using namespace std;
template <class T> inline void read(T &x){
x = 0; register char c = getchar(); register bool f = 0;
while (!isdigit(c)) f ^= c == '-', c = getchar();
while (isdigit(c)) x = x * 10 + c - '0', c = getchar();
if (f) x = -x;
}
template <class T> inline void print(T x){
if (x < 0) putchar('-'), x = -x;
if (x > 9) print(x / 10);
putchar('0' + x % 10);
}
const int N = 2e6 + 10;
int tot = 1, last = 1;
//当前用到哪个点,上一个点的编号(1表示空点)
struct Node{
int len, fa;//最长长度,绿色的边
int ch[26];//26个儿子
}node[N];
char str[N];
ll f[N], ans;//表示每一个状态的E(s)大小
int h[N], e[N], ne[N], idx;
inline void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
inline void extend(int c){
int p = last;//表示上一个状态
int np = last = ++ tot;//表示当前状态
f[tot] = 1;
node[np].len = node[p].len + 1;//新状态的长度等于旧状态加一
for(; p && !node[p].ch[c]; p = node[p].fa) //如果p没有c这个儿子就一直往父亲走
node[p].ch[c] = np;
if(!p) node[np].fa = 1;
else{
int q = node[p].ch[c];
if(node[q].len == node[p].len + 1) node[np].fa = q;
else{
int nq = ++ tot;
node[nq] = node[q], node[nq].len = node[p].len + 1;
node[q].fa = node[np].fa = nq;
for(; p && node[p].ch[c] == q; p = node[p].fa) node[p].ch[c] = nq;
}
}
}
inline void dfs(int u){
for(int i = h[u]; ~i; i = ne[i]){
dfs(e[i]);
f[u] += f[e[i]];
}
if(f[u] > 1) ans = max(ans, f[u] * node[u].len);
}
signed main(){
scanf("%s", str);
memset(h, -1, sizeof h);
for(int i = 0; str[i]; i ++) extend(str[i] - 'a');
for(int i = 2; i <= tot; i ++) add(node[i].fa, i);
dfs(1);
print(ans), puts("");
return 0;
}
玄武密码
题意:对于给定母串。询问给定子串在母串中出现的最长前缀。
思路:后缀自动机,从原点出发的所有路径,对原串的所有不同字串是一一对应的,对于任意给定字符串,在后缀自动机上一直走直道走不了,我们走的任何路径都是原串的一个子串。总结,对于任意给定串,如何判断其是不是原串的子串,只需从自动机起点开始走,能走完就是子串。
#include <map>
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#define ll long long
using namespace std;
template <class T> inline void read(T &x){
x = 0; register char c = getchar(); register bool f = 0;
while (!isdigit(c)) f ^= c == '-', c = getchar();
while (isdigit(c)) x = x * 10 + c - '0', c = getchar();
if (f) x = -x;
}
template <class T> inline void print(T x){
if (x < 0) putchar('-'), x = -x;
if (x > 9) print(x / 10);
putchar('0' + x % 10);
}
const int N = 1e7 + 10;
int n, m;
int tot = 1, last = 1;
char str[N];
struct Node{
int len, fa;
int ch[4];
}node[N * 2];
inline int get(char c){
if(c == 'E') return 0;
if(c == 'S') return 1;
if(c == 'W') return 2;
return 3;
}
inline void extend(int c){
int p = last, np = last = ++ tot;
node[np].len = node[p].len + 1;
for(; p && !node[p].ch[c]; p = node[p].fa) node[p].ch[c] = np;
if(!p) node[np].fa = 1;
else{
int q = node[p].ch[c];
if(node[q].len == node[p].len + 1) node[np].fa = q;
else{
int nq = ++ tot;
node[nq] = node[q], node[nq].len = node[p].len + 1;
node[q].fa = node[np].fa = nq;
for(; p && node[p].ch[c] == q; p = node[p].fa) node[p].ch[c] = nq;
}
}
}
signed main(){
read(n), read(m);
scanf("%s", str);
for(int i = 0; str[i]; i ++) extend(get(str[i]));
while(m --){
scanf("%s", str);
int p = 1, res = 0;
for(int i = 0; str[i]; i ++){
int c = get(str[i]);
if(node[p].ch[c]) p = node[p].ch[c], res ++;
else break;
}
print(res), puts("");
}
return 0;
}
本文作者:Altwilio
本文链接:https://www.cnblogs.com/William-Sg/p/16359520.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步