树状数组学习笔记
树状数组
树状数组是一种高效的对列表更新和求前缀和的结构
对于已经学过的前缀和(O(1)修改 O(n)查询),考虑维护一部分的区间和,修改时需要修改若干位置,查询时也需要查询若干位置,以此把修改和查询的代价平衡。
灵感
对于如何维护一部分区间,考虑每个整数为若干个 2 的幂的和,将每个前缀拆分成若干不相交的区间,按二进制中 1 的个数来拆分。
定义
对于一个合法的 BIT 区间,一定满足 [i - 2 ^ k, i],其中 k 是 i 的二进制中末尾 0 的个数,对于 BIT 数组的表示, 我们选取右端点,记原数组为 A,BIT数组为 B,有
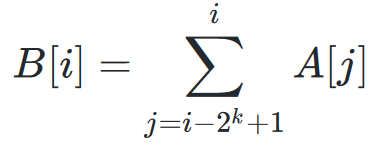
对此:
一个前缀最多包含log(n)个区间——一次查询访问log(n)个位置。
一个位置最多被log(n)个区间包含——一次修改影响log(n)个位置。
编程实现
lowbit 返回二进制下最后一个 1 所代表的数值
int lowbit(int x){
return x & (-x);
}
对于树状数组需要记住
-x == ~x + 1;
lowbit(x) = x & (-x);
单点加
inline void update(int x, int v){
for(; x <= n; x += x & -x){
tre[x] += v;
}
}
求前缀和
inline int query(int x){
int ret = 0;
for(; x; x -= x & -x){
ret += tre[x];
}
return ret;
}
建树
不需要额外空间,每一个节点都是所有与自己直接相连的儿子求和得到的,考虑倒着贡献每次确定完儿子的值,更新父亲
inline void init(){
for(int i = 1; i <= n; i ++){
tre[i] += a[i];
int j = i + lowbit(i);
if(j <= n){
tre[j] += tre[i];
}
}
}
查询
返回值为前缀和
inline int query(int x){
int res = 0;
for(; x; x -= lowbit(x))
res += tre[x];
return res;
}
模板
P3374 【模板】树状数组 1
#include<bits/stdc++.h>
using namespace std;
/*int lowbit_brute(int n){
for(int i = 0; i <= 31; i ++){
if(n & (1 << i)){
return 1 << i;
}
}
}
x & ( ~x + 1)
return n & (~n + 1);
return 1 << __builtin_ctz(n);
__builtin_ctz(n) //返回 n 的二进制末尾 0 的个数
__builtin_clz(n) //返回 n 的二进制前导 0 的个数*/
const int N = 1e6 + 5;
int tre[N], n;
int lowbit(int n){
return n & -n;
}
inline void update(int x, int v){ //第 x 位加 v
for(; x <= n; x += lowbit(x))
tre[x] += v;
}
inline int query(int x){
int res = 0;
for(; x; x -= lowbit(x))
res += tre[x];
return res;
}
inline int ask(int l, int r){
return query(r) - query(l - 1);
}
int main(){
int m;
cin >> n >> m;
for(int i = 1; i <= n; i ++){
int t; cin >> t;
update(i, t);
}
while(m --){
int op, x, k;
cin >> op >> x >> k;
if(op == 1){
update(x, k);
}
if(op == 2){
cout << ask(x, k) << endl;
}
}
}
P3368 【模板】树状数组 2
注意对原数组的差分数组建树,query返回值为当前元素
#include<bits/stdc++.h>
using namespace std;
const int N = 600010;
int n, m;
int a[N], tre[N], s[N];
inline int lowbit(int n){
return n & -n;
}
inline void update(int x, int v){
for(; x <= n; x += lowbit(x))
tre[x] += v;
}
inline void init(){
for(int i = 1; i <= n; i ++){
tre[i] += s[i];
int j = i + lowbit(i);
if(j <= n){
tre[j] += tre[i];
}
}
}
long long query(int x) {
long long ans = 0;
while (x){
ans += tre[x];
x -= lowbit(x);
}
return ans;
}
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i ++){
cin >> a[i];
}
s[1] = a[1];
for(int i = 2; i <= n; i ++){
s[i] = a[i] - a[i - 1];
}
init();
while(m --){
int op, x, y, k;
cin >> op;
if(op == 1){
cin >> x >> y >> k;
update(x, k);
update(y + 1, -k);
}else
if(op == 2){
cin >> x;
cout << query(x)<< endl;
}
}
}

