2020牛客国庆集训派对day1 B.Be Geeks! （线段树 + 区间最大值 * 区间GCD）

题目：传送门

题意

给你一个序列 A

 

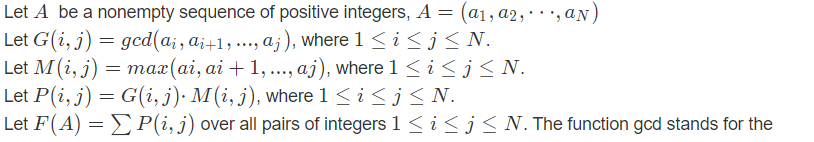
 让你求F(A)

 

 

思路

一看到这题，一般很自然的能想到两种思路：

1.枚举每个 a[i]，算出满足以当前点为最大值的区间最大区间，然后去求这个最大区间和其子区间的 gcd 的和，相乘累加起来即为答案；

2.枚举区间右端点，然后 1 ~ i 这一段会分成若干 gcd 相等的区间。算这些区间，然后求这些区间和其子区间的 max 值的和，相乘累加即为答案。

第一种，没什么想法，可行性未知，所以转向第二种。

可以用单调栈和线段树维护区间最大值的贡献，边移动右端点，边维护。

维护好了max值的贡献，接下来就是求 gcd 相等的区间了，具体实现见代码。

#include <bits/stdc++.h>
#define LL long long
#define ULL unsigned long long
#define UI unsigned int
#define mem(i, j) memset(i, j, sizeof(i))
#define rep(i, j, k) for(int i = j; i <= k; i++)
#define dep(i, j, k) for(int i = k; i >= j; i--)
#define pb push_back
#define make make_pair
#define INF 0x3f3f3f3f
#define inf LLONG_MAX
#define PI acos(-1)
#define fir first
#define sec second
#define lb(x) ((x) & (-(x)))
#define dbg(x) cout<<#x<<" = "<<x<<endl;
using namespace std;

const int N = 1e6 + 5;

const LL mod = 1e9 + 7;

int n, tot, S[N], l[N];

LL a[N], t[N], lz[N], G[N];

void push_down(int rt, int l, int r) {

    if(!lz[rt]) return ;

    int mid = (l + r) >> 1;

    t[rt << 1] = (t[rt << 1] + 1LL * (mid - l + 1) * lz[rt] % mod + mod) % mod;

    t[rt << 1 | 1] = (t[rt << 1 | 1] + 1LL * (r - mid) * lz[rt] % mod + mod) % mod;

    lz[rt << 1] = (lz[rt << 1] + lz[rt]) % mod;

    lz[rt << 1 | 1] = (lz[rt << 1 | 1] + lz[rt]) % mod;

    lz[rt] = 0;

}

void update(int rt, int l, int r, int L, int R, LL x) {

    if(L <= l && r <= R) {

        lz[rt] = (lz[rt] + x) % mod;

        t[rt] = (t[rt] + 1LL * (r - l + 1) * x % mod + mod) % mod;

        return ;

    }

    push_down(rt, l, r);

    int mid = (l + r) >> 1;

    if(L <= mid) update(rt << 1, l, mid, L, R, x);

    if(R > mid) update(rt << 1 | 1, mid + 1, r, L, R, x);

    t[rt] = (t[rt << 1] + t[rt << 1 | 1]) % mod;

}

LL query(int rt, int l, int r, int L, int R) {

    if(L <= l && r <= R) return t[rt];

    push_down(rt, l, r);

    int mid = (l + r) >> 1;

    LL ans = 0LL;

    if(L <= mid) ans = (ans + query(rt << 1, l, mid, L, R)) % mod;

    if(R > mid) ans = (ans + query(rt << 1 | 1, mid + 1, r, L, R)) % mod;

    return ans;

}

void solve() {

    scanf("%d", &n);

    rep(i, 1, n) scanf("%lld", &a[i]), l[i] = i, G[i] = a[i]; /// 初始化

    LL ans = 0LL; tot = 0;

    rep(i, 1, n) { /// 枚举区间右端点

        while(tot && a[S[tot]] < a[i]) {

            update(1, 1, n, S[tot - 1] + 1, S[tot], -a[S[tot]]); /// 以i为右端点，向左延申，栈里面比当前a[i]小的都不能作为max了，取消贡献

            tot--;

        }

        update(1, 1, n, S[tot] + 1, i, a[i]); /// 添加贡献

        S[++tot] = i;

        for(int j = i; j > 0; j = l[j] - 1) { /// 枚举 gcd 相等的段

            G[j] = __gcd(G[j], a[i]); 

            while(l[j] > 1 && __gcd(G[l[j] - 1], a[i]) == __gcd(G[j], a[i])) l[j] = l[l[j] - 1];

            ans = (ans + query(1, 1, n, l[j], j) * G[j] % mod) % mod;

        }

    }

    printf("%lld\n", ans);

}


int main() {

//    int _; scanf("%d", &_);
//    while(_--) solve();

    solve();

    return 0;
}