CF G. Running Competition (NTT, 思维)

题目：传送门

题意

在直角坐标系中，有 n + 1 条线段，第一条线段连接着 (0, 0) , (0, y)，最后一条线段连接着 (x, 0) , (x,y)，第 i 条线段，连接着 (ai, 0) , (ai, y), 0 = a0 < a1 < a2 < .... < an = n。你能从任何点开始绕着线段走，并最终回到出发点，且你不能走已经走过的点，你走过的线段的总长度就是你此次行动得到的 len.

 

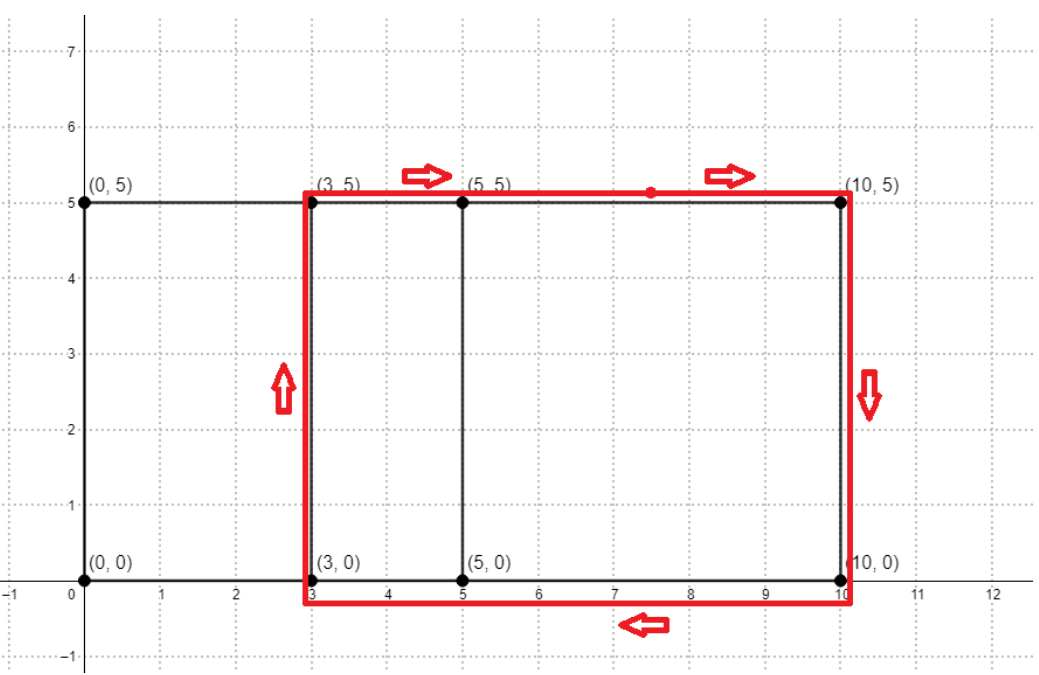
 如图，红色方框的长度即为此次行动得到的 len， 即 len = 24。

现在有 q 次询问，每次询问输入一个数 Li, 问你是否存在一种行动，使得行动得到的 len，满足 Li % len == 0，若存在输出最大的 len，不存在输出 -1.

 

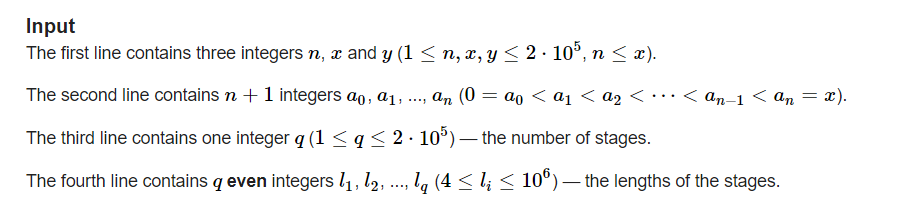
 思路

观察发现，每次行动必定是一个矩形，且其中两条边的长度等于 y，另外两条边的长度等于 ai - aj (0 <= j < i <= n).

我们令 b[i] = x - a[i]，构造两个多项式 A, B，A[i] 的第 a[i] 项的系数为 1，B[i] 的第 b[i] 项的系数为 1.

令多项式 C = A * B，多项式相乘可以用 NTT 做，复杂度 o(n*logn)

若 C[k] 的系数不为 0，则表示存在数组 a 的一个数 a[i] 和 数组 b 的一个数  b[j]  相加等于 k.

又 a[i] + b[j] = a[i] - a[j] + x，那我们可以通过判断 C[ tmp + x ] 是否不为 0，从而来判断是否存在数组 a 的两个数， a[i]，a[j]，使得 a[i] - a[j] = tmp

由于 a[i] - a[j] 的取值范围为 [1, x], 所以我们只需要枚举 k = [1,x] 判断 C[ k + x ] 是否等于 0，若不等于 0，则用 2 * (k + y) 去更新答案数组，复杂度 o(nlogn)

 

#include <bits/stdc++.h>
#define LL long long
#define ULL unsigned long long
#define UI unsigned int
#define mem(i, j) memset(i, j, sizeof(i))
#define rep(i, j, k) for(int i = j; i <= k; i++)
#define dep(i, j, k) for(int i = k; i >= j; i--)
#define pb push_back
#define make make_pair
#define INF 0x3f3f3f3f
#define inf 0x3f3f3f3f3f3f3f3f
#define PI acos(-1)
#define fir first
#define sec second
#define lb(x) ((x) & (-(x)))
#define dbg(x) cout<<#x<<" = "<<x<<endl;
using namespace std;

const int N = 1e6 + 5;

const LL G = 3;
const LL mod = 998244353;
int len, r[N];
LL g[N], f[N], w[N], x[N], y[N];
LL power(LL x,LL y) {
    LL ans = 1;
    while(y) {
        if( y & 1 ) ans = ans * x % mod;
        x = x * x % mod;
        y >>= 1;
    }
    return ans;
}
void ntt(LL *a, LL f) {
    for (LL i = 0; i < len; i++) {
        if (i < r[i]) swap(a[i], a[r[i]]);
    }
    w[0] = 1;
    for (LL i = 2; i <= len; i *= 2) {
        LL wn;
        if (f == 1) wn = power(G, (LL)(mod - 1) / i);
        else wn = power(G, (LL)(mod - 1) - (mod - 1) / i);
        for (LL j = i / 2; j >= 0; j -= 2) w[j] = w[j / 2];
        for (LL j = 1; j < i / 2; j += 2) w[j] = (w[j - 1] * wn) % mod;
        for (LL j = 0; j < len; j += i) {
            for (LL k = 0 ; k < i / 2; k++) {
                LL u = a[j + k], v = (a[j + k + i / 2] * w[k]) % mod;
                a[j + k] = (u + v) % mod;
                a[j + k + i / 2] = (u - v + mod) % mod;
            }
        }
    }
    if (f == -1) {
        LL inv = power(len, mod - 2);
        for (LL i = 0; i < len; i++) a[i] = (a[i] * inv) % mod;
    }
}
void NTT(LL *a, LL *b, LL *c, LL n, LL m) {
    len = 1;
    while (len <= (n + m)) len *= 2;
    LL k = trunc(log(len + 0.5) / log(2));
    for (LL i = 0; i < len; i++) {
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (k - 1));
    }
    for (LL i = 0; i < len; i++) {
        if (i < n) x[i] = a[i]; else x[i] = 0;
        if (i < m) y[i] = b[i]; else y[i] = 0;
    }
    ntt(x, 1); ntt(y, 1);
    for (LL i = 0; i < len; i++) c[i] = x[i] * y[i] % mod;
    ntt(c, -1);
}

LL n, X, Y, a[N];

LL A[N], B[N], ans[N];

void solve() {

    mem(ans, -1);

    scanf("%lld %lld %lld", &n, &X, &Y);

    rep(i, 0, n) {

        scanf("%lld", &a[i]);

        A[a[i]] = 1;

        B[X - a[i]] = 1;

    }

    NTT(A, B, A, X + 1, X + 1);

    rep(i, 1, X) {

        if(A[X + i]) {

            for(int j = 2 * (i + Y); j < N; j += 2 * (i + Y)) {

                ans[j] = 2 * (i + Y);

            }

        }

    }

    int q; scanf("%d", &q);

    while(q--) {

        int p; scanf("%d", &p);

        printf("%lld\n", ans[p]);

    }

}


int main() {

//    int _; scanf("%d", &_);
//    while(_--) solve();

    solve();

    return 0;
}