HDU 6755 (数论综合题，2020多校)

题目：传送门

题意

定义 Fn 为斐波那契第 n 项，递推式为

 

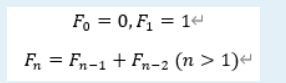
输入 N,C,K（1 <= N,C <= 1e18, 1 <= K <= 1e5）， 求

 

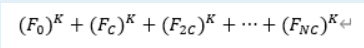
 输出答案对 1e9 + 9 取模

思路

参考博客

首先，需要知道斐波那契数列的通项公式

 

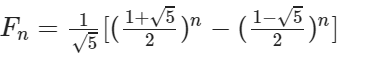
 然后我们可以用二次剩余，求出 sqrt(5) 在 mod 1e9 + 9 意义下的值，然后再对其求一下逆元，就得到 1 / sqrt(5) 在 mod 1e9 + 9 的值，这样，(1 + sqrt(5)) / 2 和 (1 - sqrt(5)) / 2 在 mod 1e9 + 9 意义下的值都可以求得。

后面的都是二项式的展开，和一些优化，这题卡常，没有优化的话会超时，具体的可以看参考博客。

 

#include <bits/stdc++.h>
#define LL long long
#define ULL unsigned long long
#define UI unsigned int
#define mem(i, j) memset(i, j, sizeof(i))
#define rep(i, j, k) for(int i = j; i <= k; i++)
#define dep(i, j, k) for(int i = k; i >= j; i--)
#define pb push_back
#define make make_pair
#define INF 0x3f3f3f3f
#define inf LLONG_MAX
#define PI acos(-1)
#define fir first
#define sec second
#define lb(x) ((x) & (-(x)))
#define dbg(x) cout<<#x<<" = "<<x<<endl;
using namespace std;

const int N = 1e6 + 5;

const LL mod = 1e9 + 9;

LL fac[N], ifac[N], n, c;

int k;

LL ksm(LL a, LL b) {

    a %= mod;

    if(b > mod) b = b % (mod - 1) + mod - 1;

    LL res = 1LL;

    while(b) {

        if(b & 1) res = res * a % mod;

        a = a * a % mod; b >>= 1;

    }

    return res;

}

LL C(int n, int m) {

    return fac[n] * ifac[m] % mod * ifac[n - m] % mod;

}

void solve() {

    scanf("%lld %lld %d", &n, &c, &k);

    LL inv_SqrtFive = 276601605; LL A = ksm(691504013, c); LL B = ksm(308495997, c);

    LL an = ksm(A, k); LL bn = 1LL; LL ifac_A = ksm(A, mod - 2);

    LL ans = 0LL;

    rep(i, 0, k) {

        LL res = an * bn % mod, tmp;

        if(res == 1LL) tmp = n % mod;

        else tmp = res * (ksm(res, n) - 1LL) % mod * ksm(res - 1, mod - 2) % mod;

        tmp = tmp * C(k, i) % mod;

        if(i & 1) ans = (ans - tmp + mod) % mod;

        else ans = (ans + tmp) % mod;

        an = an * ifac_A % mod;

        bn = bn * B % mod;

    }

    ans = ans * ksm(inv_SqrtFive, k) % mod;

    printf("%lld\n", ans);

}


int main() {

    fac[0] = 1LL;

    for(int i = 1; i <= 100000; i++) fac[i] = 1LL * i * fac[i - 1]% mod;

    ifac[100000] = ksm(fac[100000], mod - 2);

    dep(i, 0, 99999) ifac[i] = 1LL * (i + 1LL) * ifac[i + 1] % mod;

    int _; scanf("%d", &_);
    while(_--) solve();

//    solve();

    return 0;
}