HDU 3124 Moonmist （扫描线 + 二分 + 平面最近圆对的距离）

题目：传送门

题意

给你 n 个互不相交的圆的圆心和半径，问你最近的两个圆的距离是多少，T个测试。

2 <= N <= 50000  1 <= T <= 10

思路

参考博客

二分每个圆半径的增量，如果每个圆的半径增加了 mid 之后存在圆的相交，那么这个 mid 就偏大了，如果不相交，那么就是 mid 偏小了，那么就可以这样二分了。

现在，考虑怎么比较快的判断圆是否相交，这里考虑使用扫描线。

以下转载自：http://blog.sina.com.cn/s/blog_6e7b12310100qnex.html

 

 

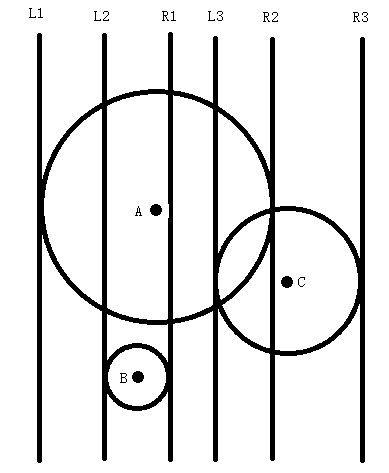
第一条扫描线从左往右依次是每个圆的左边界，即竖直线L1，L2，L3。

        第二条扫描线从左往右依次是每个圆的右边界，即竖直线R1，R2，R3。

        两条扫描线均是从最左边的L1和R1开始，保证L扫描线的x坐标永远小于R扫描线的x坐标即可。扫描流程如下，假设有n个圆，i为Li，j为Rj：

        i = j = 1

        while(i <= n or j <= n)

        {

                  if(i == n + 1) 删除圆j，j++;

                  else if (j == n + 1) 插入圆i，检测圆i的圆心和y方向相邻两圆的碰撞情况。i++。

                  else if (i <= n and Li 在Ri的左边)

                           插入圆i，检测圆i的圆心和y方向相邻两圆的碰撞情况。i++。

                  else 删除圆j，j++;

        }

简要解释如下：

While中有4个分支

前两个是边界情况，很容易理解。

第三个是L扫描线的推进，即插入圆。

第四个条件：由于只需检测Li 和 Rj两条扫描线之间的圆的相交情况，所以，Li之前的圆都需要删除

当扫描线为Li和Rj时，已经插入的圆都是x方向起点小于等于Li，x方向终点大于等于Rj，即在Li和Rj之间是连续不间断的，所以只需检测插入圆的圆 心的上下相邻的两个即可，不可能跳跃。即假设圆心位置从下到上一次编号1~m，那么插入圆x后，不可能出现x和x+2相交而不和x+1相交的情况（应为在 Li和Rj之间是连续的）。

至于检测的方法就是线段树或者set了。

上图的扫描线过程是：

初始为L1,R1

L1 < R1, 插入圆A，检测无碰撞，变为L2，R1

L2 < R1, 插入圆B，检测无碰撞，变为L3, R1

L3 > R1, 删除圆B，变为L3，R2

L3 < R2，插入圆C，检测到碰撞，结束

 

 

#include <bits/stdc++.h>
#define LL long long
#define ULL unsigned long long
#define mem(i, j) memset(i, j, sizeof(i))
#define rep(i, j, k) for(int i = j; i <= k; i++)
#define dep(i, j, k) for(int i = k; i >= j; i--)
#define pb push_back
#define make make_pair
#define INF INT_MAX
#define inf LLONG_MAX
#define PI acos(-1)
#define fir first
#define sec second
using namespace std;

const int N = 1e6 + 5;
const double eps = 1e-10;

struct Point {
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) { }
};

Point operator + (Point A, Point B) { return Point(A.x + B.x, A.y + B.y); }
Point operator - (Point A, Point B) { return Point(A.x - B.x, A.y - B.y); }
Point operator * (Point A, double p) { return Point(A.x * p, A.y * p); }
Point operator / (Point A, double p) { return Point(A.x / p, A.y / p); }
double Cross(Point A, Point B) { return A.x * B.y - A.y * B.x; }
double Dot(Point A, Point B) { return A.x * B.x + A.y * B.y; }
double Length(Point A) { return sqrt(Dot(A, A)); }

int dcmp(double x) {
    if(fabs(x) < eps) return 0; return x < 0 ? -1 : 1;
}

bool operator < (Point A, Point B) {
    return A.x < B.x || (A.x == B.x && A.y < B.y);
}

double x[N], y[N], r[N], mid;
int L[N], R[N], ran[N], ran_pos[N], n;

bool cmpL(int a, int b) {
    return x[a] - r[a] < x[b] - r[b];
}
bool cmpR(int a, int b) {
    return x[a] + r[a] < x[b] + r[b];
}
bool cmpran(int a, int b) {
    return y[a] < y[b] || (y[a] == y[b] && x[a] < x[b]);
}

set < int > Q;

bool ok(int a, int b) {
    a = ran[a];
    b = ran[b];
    double tmp1 = Dot(Point(x[a], y[a]) - Point(x[b], y[b]), Point(x[a], y[a]) - Point(x[b], y[b]));
    double tmp2 = (r[a] + r[b] + mid + mid) * (r[a] + r[b] + mid + mid);
    if(tmp1 <= tmp2) return true;
    else return false;
}

bool add(int a) {
    set < int > :: iterator it;
    it = Q.insert(a).first; /// first指向当前插入的点的位置
    if(it != Q.begin()) {
        if(ok(a, *--it)) return true;
        it++;
    }
    if(++it != Q.end()) {
        if(ok(a, *it)) return true;
    }
    return false;
}

bool judge() {
    Q.clear();
    int i = 1, j = 1;
    while(i <= n || j <= n) {
        if(j == n + 1 || (i != n + 1 && x[L[i]] - r[L[i]] - mid < x[R[j]] + r[R[j]] + mid)) {
            if(add(ran_pos[L[i++]])) return true;
        }
        else Q.erase(ran_pos[R[j++]]);
    }
    return false;
}

void get_ans() {
    double nowl = 0, nowr = Dot(Point(x[1], y[1]) - Point(x[2], y[2]), Point(x[1], y[1]) - Point(x[2], y[2])) - r[1] - r[2];
    while(nowr - nowl > eps) {
        mid = (nowl + nowr) * 0.5;
        if(judge()) nowr = mid;
        else nowl = mid;
    }

    printf("%.6f\n", nowl + nowr);
}

void solve() {
    scanf("%d", &n);

    rep(i, 1, n) {
        scanf("%lf %lf %lf", &x[i], &y[i], &r[i]);
        L[i] = R[i] = ran[i] = i;
    }
    sort(L + 1, L + 1 + n, cmpL);
    sort(R + 1, R + 1 + n, cmpR);
    sort(ran + 1, ran + 1 + n, cmpran);
    rep(i, 1, n) ran_pos[ran[i]] = i;

    get_ans();

}

int main() {
    int _; scanf("%d", &_);
    while(_--) solve();

    return 0;
}

 

 

有注释的代码：出处

 

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <math.h>
#include <set>
#include <algorithm>
using namespace std;
#define left Left
#define right Right
#define eps 1e-8
#define maxn 60000
double x[maxn],y[maxn],r[maxn];
int left[maxn],right[maxn],up[maxn],rank_up[maxn];
int n;
set<int> my_set;
double mid;
bool cmp_left(const int &a,const int &b)
{
    return x[a]-r[a] < x[b]-r[b];
}
bool cmp_right(const int &a,const int &b)
{
    return x[a]+r[a] < x[b]+r[b];
}
bool cmp_up(const int &a,const int &b)
{
    if(y[a]==y[b])
    return  x[a] < x[b];
    else return y[a] < y[b];
}
double my_sqr(double a)
{
    return a*a;
}
bool is_cross(int a,int b)//檢測高度排名為a和b的圓是否相交
{
    a=up[a],b=up[b];
    double t1,t2;
    t1=my_sqr(x[a]-x[b])+my_sqr(y[a]-y[b]),t2=my_sqr(r[a]+r[b]+mid+mid);
    if(t1<=t2)
    return true;//表示相交
    return false;
}
/*
 * 這個函數插入的是當前在集合裡面圓心y值，每次再插入
 * 的同時返回插入的位置，由於set是排序了的，所以前後相鄰位置
 * 的大小關係也是相鄰的，那麼在檢測當前插入的這個圓是否與當前集合裡面的圓相交
 * 就只要判斷當前插入的圓與其上下兩個圓是否相交就OK了
 */
bool insert(int a)//這個函數在插入的同時檢測是否發生相交的情況
{
    set<int>::iterator it=my_set.insert(a).first;//這個first指向當前插入的這個元素位置的迭代器
    if(it!=my_set.begin())
    {
        if(is_cross(a,*--it))//相交
        return true;
        it++;//恢復
    }
    //注意set開始位置是元素，結束位置是位置，所以處理起來就不同了
    if(++it!=my_set.end())
    {
        if(is_cross(a,*it))
        return true;
    }
    return false;
}
bool is_ok()
{
    my_set.clear();
    int i=0,j=0;
    while(i<n || j<n)
    {
        if(j==n ||(i!=n && x[left[i]]-r[left[i]]-mid<x[right[j]]+r[right[j]]+mid))
        {
            /*這裡代碼在處理的時候插入的是y坐標的排名，這樣的好處是插入set是
             *排序的，這樣就能保證set某個元素的前後位置就是在真實圓的上下相鄰位置，所以這裡每次插入的是排名
             *也就是插入的不是元素，是排名，在插的時候直接插你排第幾
             */
            if(insert(rank_up[left[i++]]))
                return true;//
        }
        else
        my_set.erase(rank_up[right[j++]]);
    }
    return false;
}
double find_ans()
{
    double l=0,ri=sqrt(my_sqr(x[0]-x[1])+my_sqr(y[0]-y[1]))-r[0]-r[1];///求最小的距離嘛，左值為0，右邊隨便取一個兩個圓距離就OK了
    while(l+eps<ri)///這裡不加eps可能對於某些測試數據導致超時
    {
        mid=(l+ri)/2;
        if(is_ok())
        ri=mid;
        else
        l=mid;
    }
    printf("%.6lf\n",l+ri);
    return 0;
}
int main()
{
    int t,i,j,k;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        for(i=0;i<n;i++)
        scanf("%lf%lf%lf",&x[i],&y[i],&r[i]);
        for(i=0;i<n;i++)
        {
            left[i]=i;
            right[i]=i;
            up[i]=i;
        }
        sort(left,left+n,cmp_left);
        sort(right,right+n,cmp_right);
        sort(up,up+n,cmp_up);
        for(i=0;i<n;i++)
        rank_up[up[i]]=i;
        find_ans();
    }
    return 0;
}