F. Moving Points （树状数组）

题目： 传送门

题意： 有 n 个点在 x 轴上，最初他们在 xi 上，第 1 秒后它就移动到 xi + vi，第 t 秒就移动到 xi + t * vi 上。定义 d(i, j) = 点 i 和点 j 在移动的过程中，最近的距离。要你求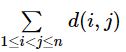

　　　2 <=  n <= 2e5； 1 <= xi <= 1e8;    -1e8 <= vi <= 1e8

 

解： 每个点的移动轨迹都可以用一条直线 y = kx + b 表示，最初的时候在 xi 上，即 x = 0 时， y = xi，那么 b 就等于 xi，k 显然就是 vi 了。

　　 如果两条直线相交，且交点处 x >= 0，这两个点的 d(i, j) 就等于0，否则，这两个点的 d(i, j) 就等于 abs( xi - xj )，因为随着 t 增加，他们的距离只会越来越大。

　　

 

 

 　　

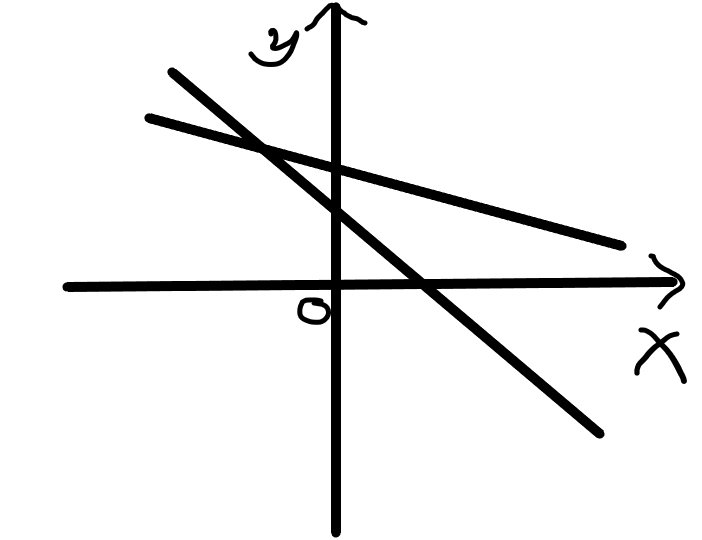
总结一下就是，若两直线的交点在 x 轴的负半轴， d(i, j) = abs( xi - xj )，否则 d( i, j ) = 0

这个交点的 x 怎么求呢，你联立一下两个方程：

y = vi*x + xi

y = vj*x + xj

得 x = (xj - xi) / (vi - vj)；

发现当 vi = vj 时无解，这个时候两直线是平行的，那也当作交点在 x 负半轴处理。

要使得 x <= 0 则需 xi <= xj 且 vi <= vj 或 xj <= xi && vi <= vj；

我们只要对每个点按 x 排序，然后维护一个树状数组存 vi <= vj 的数的个数和他们的 x 的总和。

考虑到 vi 的范围比较大，需要离散化一下。

每个点 i 对答案的贡献就是， v 小于等于 vi 的点个数 * x[ i ] - v 小于等于 vi 的点的 x 的和，累加起来即可。

 

#include <bits/stdc++.h>
#define LL long long
#define mem(i, j) memset(i, j, sizeof(i))
#define rep(i, j, k) for(int i = j; i <= k; i++)
#define dep(i, j, k) for(int i = k; i >= j; i--)
#define pb push_back
#define make make_pair
#define INF INT_MAX
#define inf LLONG_MAX
#define PI acos(-1)
using namespace std;

const int N = 2e5 + 5;

pair < LL, LL > a[N];
LL b[N];

LL s1[N], s2[N];

void add(int pos, LL x) {
    while(pos <= N - 5) {
        s1[pos]++; s2[pos] += x;
        pos += pos & (-pos);
    }
}

LL query(LL s[], int pos) {
    LL res = 0LL;
    while(pos > 0) {
        res += s[pos];
        pos -= pos & (-pos);
    }
    return res;
}

int main() {
    int n; scanf("%d", &n);
    rep(i, 1, n) scanf("%lld", &a[i].first);
    rep(i, 1, n) scanf("%lld", &a[i].second), b[i] = a[i].second;
    sort(b + 1, b + 1 + n); sort(a + 1, a + 1 + n);
    int m = unique(b + 1, b + 1 + n) - (b + 1);
    LL ans = 0LL;
    rep(i, 1, n) {
        int pos = lower_bound(b + 1, b + 1 + m, a[i].second) - b;
        LL sum1 = query(s1, pos); LL sum2 = query(s2, pos);
        LL tmp = sum1 * a[i].first - sum2;
        ans = ans + tmp;
        add(pos, a[i].first);
    }
    printf("%lld\n", ans);
    return 0;
}