E. Optimal Polygon Perimeter (思维)

题目： 传送门

题意： 给你一个凸包，定义 dis(Point a, Point b) 为 a 点和 b 点的曼哈顿距离；定义 f(x) 为选定 x 个点，Point1, Point2 ..... Pointx 的 dis(Point 1, Point 2) + dis(Point 2, Point 3) + ...... + dis(Point x, Point 1) 的最大值。 请你输出 f(3) .... f(n)。

 

解： 首先， 对于选 4 个点及其以上的情况来说，肯定是刚好包围这个凸包的矩形的周长。

　　 

 

 

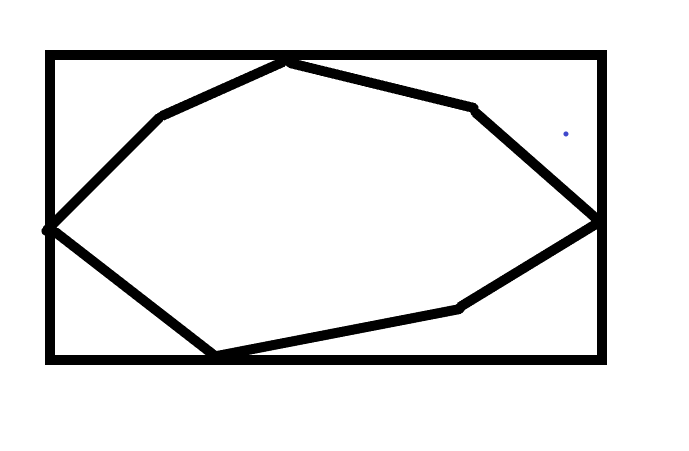
　　那我们直接求最大的 x，y 和最小的 x， y 即可。

　　然后考虑选 3 个点的情况。 选三个点， 组成一个三角形。那就有四种情况：

　　①、选最大的 x 和 最大的 y

　　②、选最大的 x 和最小的 y

　　③、选最小的 x 和最大的 y

　　④、选最小的 x 和最小的 y

　　然后再枚举第三个点维护一个最大值即可。

　　这里不考虑， 选最大的 x 和最小的 x 的原因是，选最大的 x 和最小的 x，那么第三个点肯定是 最小的 y 或者最大的 y 其中一个。

　　那我们选最大的 x 和最小的 y 的时候是会枚举到最小的 x 这种情况的， 所以只需考虑以上四种情况即可。

　　

#include <bits/stdc++.h>
#define LL long long
#define mem(i, j) memset(i, j, sizeof(i))
#define rep(i, j, k) for(int i = j; i <= k; i++)
#define dep(i, j, k) for(int i = k; i >= j; i--)
#define pb push_back
#define make make_pair
#define INF INT_MAX
#define inf LLONG_MAX
#define PI acos(-1)
using namespace std;

const int N = 1e6 + 5;

int x[N], y[N];



int main() {
    int n; scanf("%d", &n);
    int smallx = INF, bigx = -INF, smally = INF, bigy = -INF;
    rep(i, 1, n) {
        scanf("%d %d", &x[i], &y[i]);
        smallx = min(smallx, x[i]);
        bigx = max(bigx, x[i]);
        smally = min(smally, y[i]);
        bigy = max(bigy, y[i]);
    }
    int ans = 0;
    rep(i, 1, n) {
        ans = max(ans, bigx - x[i] + bigy - y[i]);
        ans = max(ans, bigx - x[i] + y[i] - smally);
        ans = max(ans, x[i] - smallx + bigy - y[i]);
        ans = max(ans, x[i] - smallx + y[i] - smally);
    }
    printf("%d ", ans * 2);
    rep(i, 4, n) printf("%d ", 2 * ((bigx - smallx) + (bigy - smally)));
    return 0;
}