初识Haskell 三：函数function

对Discrete Mathematics Using a Computer的第一章Introduction to Haskell进行总结。环境Windows

---

函数毫无疑问是函数式语言的核心。

在Haskell中（无特殊指明，以下皆是指在Haskell下），一个表达式用函数完成计算被称为a function application，函数后加空格然后跟随参数(arguments)，如有多个参数，也以空格作为分隔。

函数的返回值即函数的类型，如一个函数的参数是类型a，返回值是类型b，写作a → b（在Haskell中用 -> 表示），读作a arrow b。

操作符其实也是函数，它有2个参数，写在2个参数中间，其实也可以像正常函数一样写在前面，但需要加( )如：

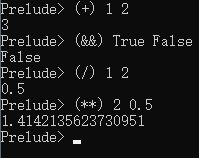
同样的，也可以像对待操作符一样将函数放在2个参数中间，但要加反引号( single-back-quote, ` )，如：

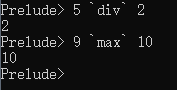
将函数定义在Haskell脚本文件(.hs)中，载入(在ghci中 :load)后，即可使用。

函数的声明：

　　function_name :: argType₁ -> argType₂ ->  ... ->argType_n ->resultType

函数体：

　function_name arg₁ arg₂ ... arg_n = expression that can use the arguments

　　

模式匹配pattern matching

在定义函数时，为应对不同情况，可以有多个函数体，如：f :: Integer -> String

f 1 = "one"
f 2 = "two"
f 3 = "three"

is_three :: Int->Bool

is_three 3 = False

is_three x = True --这里的x代表任何Int值，但由于是第二条执行到这一条就代表了x不是3

　　在得到参数执行时，会从第一条开始比较是否符合，当遇到符合的才会执行，执行后即该函数执行完成，如果没有符合的会报错，如：

元组和list都可以作为函数参数，其中list有两种形式：

1. [1,2,3, x ] 　　-- 表示list中有具体个数

2. x:xs　　　　  -- 表示至少有1个元素的list

3. xs　　　　　 -- 通用的list，包括空list

当用x:xs的时候，可以使用@来给整个列表命名，如lst@(x:xs)，则在之后的代码中可用lst来指代(x:xs)。

练习题：

　　我的答案：

exercise3 :: Char -> Bool
exercise3 'a' = True
exercise3 x = False

exercise4 :: String -> Bool
exercise4 "hello" = True
exercise4 x = False

exercise5 :: String -> String
exercise5 (' ':xs) = xs
exercise5 xs = xs

 另一种应对多种值的方法：guards。即使用bool表达式判断是否符合条件，符合则执行该行。

fact :: Integer -> Integer
fact n
    | n < 0   = 0
    | n == 0 = 1 
    | otherwise = n * fact (n - 1)

 

 

高阶函数higher order functions

　　参数和返回值都是正常的数据类型则该函数是一阶函数(first order)。以别的函数作为参数或者以其他函数作为返回结果则是高阶函数(higher order)。如：

twice :: (a -> a) -> a -> a
twice f x = f (f x)

 

函数是一次接收一个函数进行处理的，比如一个需要2个参数的函数 ，如果只给出第一个参数，那么返回的是一个需要一个参数来完成原函数的新函数(partial application)。

prod :: Integer -> Integer ->Integer
prod x y = x * y

g = prod 4
p = g 6
q = twice g 3

 

条件表达式conditional expressions

样式：

if Boolean_expression then exp1 else exp2   --then和else都必须要有，exp1和exp2的type一样。

局部变量local variables: let Expressions

　　当某个固定式子被多次使用时，为了方便可以定义为局部变量。

　　样式：

　　　　let  equation

　　　　　　equation

　　　　　　...

　　　　　　equation

　　　　in　expression

　　上式的值为in后的expression。以求一元二次方程程序为例，要注意Tab缩进：

quadratic :: Double -> Double -> Double -> (Double, Double)
quadratic a b c = 
    let d = sqrt (b^2 - 4 * a * c)
        x1 = (-b + d) / (2 * a)
        x2 = (-b -d) / (2 * a)
    in (x1, x2)

 要注意从let到in expression，其整体就是一个表达式，如下所示：

let x = sqrt 9 in (x + 1) * (x - 1)的值为8.0(x的值为3.0)，所以2 + let x = sqrt 9 in (x + 1) * (x - 1)的值为10.0。

case

 

 

局部变量local variables: where

　　另一种表达局部变量作为helper是where。如：

　　maximum :: [Int] -> Int

　　maximum [x] = x
　　maximum (x:xs)
　　　　| x > maxxs = x
　　　　| otherwise = maxxs
　　　　where maxxs = maximum xs

类型变量type variables

　　类似与Java中的泛型generics，在定义函数时不明确其类型，在应用时，根据传入参数的类型确定，这样就只要定义一个函数就可以应对多种不同类型，而不用为了类型不同，一一重复定义函数，体现了其多态性，在之前的例子中也有没有指明其类型而是用字母代替的，比如

fst :: (a, b) -> a
snd :: (a, b) -> b

 类型变量必须以小写字母开头，通常用a,b...