排序算法(sorting)
学习到的排序算法的总结,包括对COMP20003中排序部分进行总结,部分图片来自COMP20003
有部分内容来自http://www.cnblogs.com/eniac12/p/5329396.html
演示动画:https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html
概念:
stable sort: 相同的值排序后相对顺序不变。

Comparison-based sorting is Ω(nlogn).
Hash function ---
用数对list中的元素求余,根据余值放入对应的桶(bucket)中,使用素数(prime)能使得分配更为均匀。
Collisions冲突:两个元素的余值相同时发生。当buckets数量<元素数量,则一定发生。1个好的hash function应尽量少出现collison,但不能认为collision不会发生,换言之要做好应对。
Collision Resolution Methods
1.Chaining
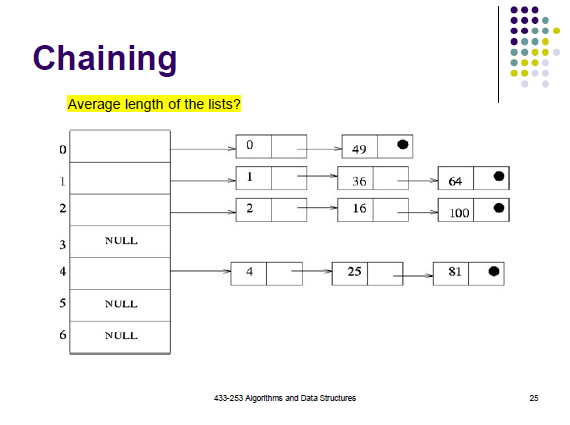

最坏情况:所有值都在同一bucket,实际上为linked list。
2.Open addressing methods
-
- Linear probing
当插入位置已有数据时,插入下一空余位置(循环),若全满了,则collision。
-
- Double hashing
当插入位置已有数据时,进行第二次求余得出新的位置。注意第二次求余值要+1避免在仍在原地。

Distribution counting --- unusual approach to sorting
计数排序(Counting sort):
requires: Key values to be within a certain range, lower to upper. 要排序的值在一定范围内。
通过记录所有数中,比该数小的有几个,来安排其位置。可以用辅助数组(auxiliary array)记录范围内比该值小(大)的有几个,也可以用for循环。用于整数排序。

1 #include <stdio.h> 2 #include <stdlib.h> 3 4 int *countSort(int *n, int size); 5 int *countSortIterative(int *n, int size); 6 void printArray(int *n, int size); 7 int min(int *n, int size); 8 int max(int *n, int size); 9 10 int main(int argc, char **argv) { 11 int size = 16; 12 int unsortedArray[16] = {4,4,2,2,0,2,1,3,2,4,3,1,4,3,1,4}; 13 int *sortedArray = NULL; 14 printArray(unsortedArray, size); 15 //sortedArray = countSort(unsortedArray, size); 16 sortedArray = countSortIterative(unsortedArray, size); 17 printArray(sortedArray, size); 18 free(sortedArray); 19 return 0; 20 } 21 22 void printArray(int *n, int size) { 23 int i = 0; 24 for (i = 0; i < size; i++) { 25 printf("%d ", n[i]); 26 } 27 printf("\n"); 28 } 29 30 int *countSortIterative(int *n, int size) { 31 int i = 0, j = 0; 32 int *sortedArray = NULL; 33 int count = 0; 34 35 if((sortedArray = (int *) calloc(size, sizeof(int))) == NULL) { 36 printf("calloc error\n"); 37 exit(EXIT_FAILURE); 38 } 39 40 for (i = 0; i < size; i++) { 41 for (j = 0, count = 0; j < size; j++) { 42 if (i == j) { 43 continue; 44 } 45 if (n[i] > n[j]) { 46 count++; 47 } 48 if (i > j && n[i] == n[j]) { 49 count++; 50 } 51 } 52 sortedArray[count] = n[i]; 53 } 54 return sortedArray; 55 } 56 57 int *countSort(int *n, int size) { 58 int rangeFrom, rangeTo; 59 int *cumulativeRecord = NULL; 60 int *sortedArray = NULL; 61 int i = 0; 62 63 rangeFrom = min(n, size); 64 rangeTo = max(n, size); 65 printf("size is %d, min is %d, max is %d\n", size, rangeFrom, rangeTo); 66 67 if((cumulativeRecord = (int *) calloc(rangeTo - rangeFrom + 1, sizeof(int))) == NULL) { 68 printf("calloc error\n"); 69 exit(EXIT_FAILURE); 70 } 71 for (i = 0; i < size; i++) { 72 cumulativeRecord[n[i] - rangeFrom]++; 73 } 74 for(i = 0; i < rangeTo - rangeFrom + 1; i++) { 75 if (i == 0) { 76 continue; 77 } 78 cumulativeRecord[i] = cumulativeRecord[i] + cumulativeRecord[i - 1]; 79 } 80 //printArray(cumulativeRecord, rangeTo - rangeFrom + 1); 81 if((sortedArray = (int *)malloc(size * sizeof(int))) == NULL) { 82 printf("malloc error\n"); 83 exit(EXIT_FAILURE); 84 } 85 86 for ( i = 0; i < size; i++) { 87 sortedArray[cumulativeRecord[n[i] - rangeFrom]-1] = n[i]; 88 cumulativeRecord[n[i] - rangeFrom] --; 89 } 90 //printArray(sortedArray, size); 91 free(cumulativeRecord); 92 return sortedArray; 93 } 94 95 int min(int *n, int size) { 96 int i = 0; 97 int min = n[0]; 98 for (i = 1; i < size; i++) { 99 if (min > n[i]) { 100 min = n[i]; 101 } 102 } 103 return min; 104 } 105 int max(int *n, int size) { 106 int i = 0; 107 int max = n[0]; 108 for (i = 1; i < size; i++) { 109 if (max < n[i]) { 110 max = n[i]; 111 } 112 } 113 return max; 114 }
复杂度:O(n) (non-comparison-based)
冒泡排序Bubble sort
使用双循环逐个对相邻元素进行比较,将较大(小)的元素放在后面,经过一次循环,最大(小)的元素被排到末尾。该方法就如名字一般,将较大(小)的浮上来。
worst case: O(n^2)
best case: O(n) 如果设一flag变量检测有无进行元素交换,则在已按顺序排好的list中,第一次循环时,没有进行交换而停止。
average case: O(n^2)
stable sort

1 /* sort the array from min to max 2 worst case: O(n^2) 3 best case: O(n) if set a flag to detect whether swap the elements 4 average case: O(n^2) 5 stable sort 6 */ 7 8 #include <stdio.h> 9 10 void swap(int *array, int a, int b) { 11 int temp = array[a]; 12 array[a] = array[b]; 13 array[b] = temp; 14 } 15 16 void bubbleSort(int *array, int size) { 17 int i, range, swapFlag = 0; 18 19 for (range = size - 1; range > 0; range--) { 20 for (i = 0; i < range; i++) { 21 if (array[i] > array[i + 1]) { 22 swap(array, i, i + 1); 23 swapFlag = 1; 24 } 25 } 26 if (swapFlag == 0) { 27 break; 28 } 29 } 30 } 31 32 int main(int argc, char **argv) { 33 int array[] = {4, -2, 2, 9, 10, 3}; 34 int i; 35 bubbleSort(array, 6); 36 for (i = 0; i < 6; i++) { 37 printf("%d ", array[i]); 38 } 39 printf("\n"); 40 return 0; 41 }
选择排序Selection sort
选择排序是一种简单直观的排序算法。它的工作原理很容易理解:初始时在序列中找到最小(大)元素,放到序列的起始位置作为已排序序列;然后,再从剩余未排序元素中继续寻找最小(大)元素,放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
注意选择排序与冒泡排序的区别:冒泡排序通过依次交换相邻两个顺序不合法的元素位置,从而将当前最小(大)元素放到合适的位置;而选择排序每遍历一次都记住了当前最小(大)元素的位置,最后仅需一次交换操作即可将其放到合适的位置。
worst case: O(n^2)
best case: O(n^2)
average case: O(n^2)
unstable sort:
选择排序是不稳定的排序算法,不稳定发生在最小元素与A[i]交换的时刻。
比如序列:{ 5, 8, 5, 2, 9 },一次选择的最小元素是2,然后把2和第一个5进行交换,从而改变了两个元素5的相对次序。

1 #include <stdio.h> 2 3 /* sort the array from min to max 4 worst case: O(n^2) 5 best case: O(n^2) 6 average case: O(n^2) 7 unstable sort 8 */ 9 void selectionSort(int *array, int size); 10 void swap(int *array, int a, int b); 11 void printArray(int *n, int size); 12 13 int main(int argc, char **argv) { 14 int array[10] = {10,9,7,8,6,5,4,3,2,1}; 15 printArray(array, 10); 16 selectionSort(array, 10); 17 printArray(array, 10); 18 return 0; 19 } 20 21 /* sort the array from min to max */ 22 void selectionSort(int *array, int size) { 23 int i, j, min; 24 25 for (i = 0; i < size - 1; i++) { 26 min = i; 27 for (j = i + 1; j < size; j++) { 28 if (array[min] > array[j]) { 29 min = j; 30 } 31 } 32 if (i != min) { 33 swap(array, i, min); 34 } 35 } 36 } 37 38 void swap(int *array, int a, int b) { 39 int temp = array[a]; 40 array[a] = array[b]; 41 array[b] = temp; 42 } 43 44 void printArray(int *n, int size) { 45 int i = 0; 46 for (i = 0; i < size; i++) { 47 printf("%d ", n[i]); 48 } 49 printf("\n"); 50 }
插入排序Insertion sort
类似于打扑克时抽牌时的操作,抽到第n张时,与前一张比较大小,直到前一张的牌比第n张小,则插入此位置。
worst case O(n^2)
average case O(n^2)
best case O(n): 当list已经拍好顺序时。
stable sort

1 #include <stdio.h> 2 /* sort the array from min to max 3 worst case O(n^2) 4 average case O(n^2) 5 best case O(n) 6 stable sort 7 */ 8 void insertionSort(int *array, int size); 9 void printArray(int *n, int size); 10 11 int main(int argc, char **argv) { 12 int array[10] = {-9, 10, 2, 3, -4, 4, 8, 12, 15, 7}; 13 printArray(array, 10); 14 insertionSort(array, 10); 15 printArray(array, 10); 16 return 0; 17 } 18 19 void insertionSort(int *array, int size) { 20 int i = 1, j, insertionVal; 21 for (i = 1; i < size; i++) { 22 insertionVal = array[i]; 23 j = i; 24 while( j - 1 >= 0 && array[j - 1] > insertionVal) { 25 array[j] = array[j - 1]; 26 j--; 27 } 28 array[j] = insertionVal; 29 } 30 } 31 32 void printArray(int *n, int size) { 33 int i = 0; 34 for (i = 0; i < size; i++) { 35 printf("%d ", n[i]); 36 } 37 printf("\n"); 38 }
分治策略(divide-and-conquer sorting algorithm):
快速排序(Quicksort)---Hard split, easy join:
Partition array:
Pick Pivot, which it is in its final position
Everything larger than pivot has higher index
Everything less than pivot has lower index
选择一个pivot枢纽(?不知道中文该对应哪个),可以是最左边或最右边等由自己决定,根据pivot的选择不同,会有不同效果。比pivot大的排在pivot右边,小的排在左边,只是如此,在左边的和右边的序列并未按序。
Recursion:
Partition left-half(recursively)
Partition right-half(recursively)
Base case:singletons are already sorted
如此不断递归。
注意:在选择pivot时,最后将pivot放置到正确位置,如选择最左作为pivot,在partition时,最后将从右开始筛选的替换。
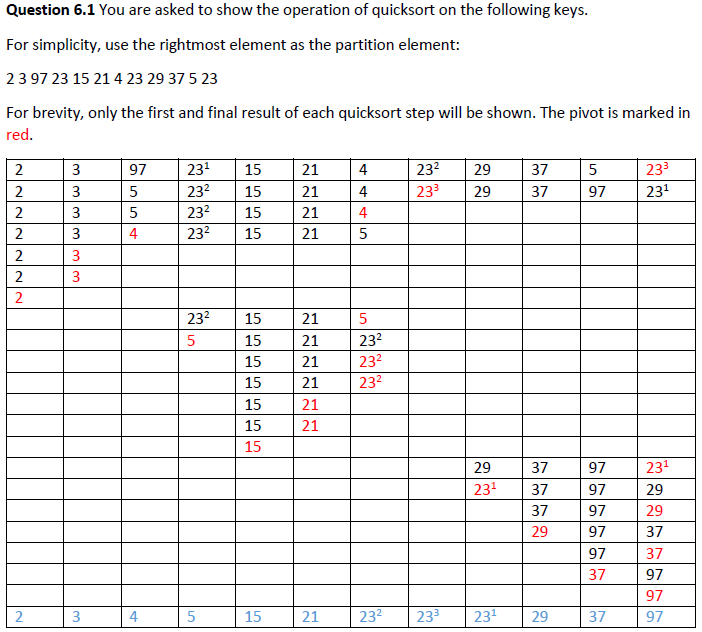

1 #include <stdio.h> 2 #include <stdlib.h> 3 4 void quicksort(int *n, int l, int r); 5 void printArray(int *n, int i); 6 int partition(int *n, int l, int r); 7 int partitionLeft(int *n, int l, int r); 8 int partitionRight(int *n, int l, int r); 9 void swap(int *n, int i, int j); 10 11 int main(int argc, char **argv) { 12 int *n = (int *) malloc(sizeof(int)); 13 int i = 0; 14 int data; 15 while (scanf("%d", &data) == 1) { 16 n = realloc(n, sizeof(int) * (i + 1)); 17 n[i] = data; 18 i++; 19 } 20 printArray(n, i); 21 quicksort(n, 0, i - 1); 22 23 printArray(n, i); 24 free(n); 25 return 0; 26 } 27 28 void printArray(int *n, int i) { 29 int j = 0; 30 for (j = 0; j < i; j++) { 31 printf("%d ", n[j]); 32 } 33 printf("\n"); 34 } 35 36 void quicksort(int *n, int l, int r) { 37 int i; 38 if (l >= r) { 39 return; 40 } 41 i = partition(n, l, r); 42 quicksort(n, l, i - 1); 43 quicksort(n, i + 1, r); 44 } 45 46 int partition(int *n, int l, int r) { 47 return partitionLeft(n, l, r); 48 //return partitionRight(n, l, r); 49 } 50 51 int partitionLeft(int *n, int l, int r) { 52 int pivot = n[l]; 53 int left = l; 54 int right = r + 1; 55 while(1) { 56 do{ 57 left++; 58 } while(n[left] < pivot); 59 do{ 60 right--; 61 } while(n[right] > pivot); 62 63 if (left >= right) { 64 break; 65 } 66 swap(n, left, right); 67 } 68 swap(n, l, right); 69 return right; 70 } 71 72 int partitionRight(int *n, int l, int r) { 73 int pivot = n[r]; 74 int left = l - 1; 75 int right = r; 76 while(1) { 77 do{ 78 left++; 79 } while(n[left] < pivot); 80 do{ 81 right--; 82 } while(n[right] > pivot); 83 84 if (left >= right) { 85 break; 86 } 87 swap(n, left, right); 88 } 89 swap(n, r, left); 90 return left; 91 } 92 93 void swap(int *n, int i, int j) { 94 int temp = n[i]; 95 n[i] = n[j]; 96 n[j] = temp; 97 }
归并排序(Mergesort)---Easy split, hard join:
关键:当有两个已排好顺序的list(array or linked list)要合并(merge)成一个时,使用两个指针分别指向两个lists,比较其大小,小的放入新list,其对应指针指向下一个,直到两个lists都装入新list。

1 /* merge two sorted arrays, first -- mid, mid + 1 -- last */ 2 void merge(int *array, int first, int mid, int last) { 3 int newArray[last - first + 1]; 4 int i, j, k; 5 for (i = first, j = mid + 1, k = 0; k < last - first + 1; k++) { 6 if (i > mid) { 7 newArray[k] = array[j++]; 8 continue; 9 } 10 if (j > last) { 11 newArray[k] = array[i++]; 12 continue; 13 } 14 if (array[i] < array[j]) { 15 newArray[k] = array[i++]; 16 } else { 17 newArray[k] = array[j++]; 18 } 19 } 20 21 /* paste newArray to array */ 22 for (i = first, k = 0; i <= last ; i++, k++) { 23 array[i] = newArray[k]; 24 } 25 }
分为两种:1.Top-down mergesort(recursive)
将list不断一分为二,直到分成单个为止,然后开始合并,使用递归。

1 void mergeSortRecursion(int *array, int first, int last) { 2 int mid = (first + last) / 2; 3 4 if (first == last) { 5 return; 6 } 7 mergeSortRecursion(array, first, mid); 8 mergeSortRecursion(array, mid + 1, last); 9 merge(array, first, mid, last); 10 }
2.Bottom-up mergesort(iterative)
将list看作是由单个元素的lists组成的,两两合并,使用迭代。

1 void mergeSortIterative(int *array, int len) { 2 int i, first, mid, last; 3 for (i = 1; i < len; i *= 2) { 4 first = 0; 5 while(first + i < len) { 6 mid = first + i - 1; 7 last = mid + i < len ? mid + i : len - 1; 8 merge(array, first, mid, last); 9 printf("first = %d, mid = %d, last = %d\n", first, mid, last); 10 first = last + 1; 11 } 12 printArray(array, len); 13 } 14 }
使用链表完成的bottom-up mergesort(iterative)放在了我的github:https://github.com/Will-Zhu-27/Algorithms-and-Data-Structures/tree/master/sorting/merge%20sort%20in%20linked%20list






