关于树及其各种操作
对树的知识进行整理，图片来自COMP20003。
首先树(tree)并不一定都是二叉树(binary tree)，这里主讲二叉树。
二叉树：
二叉树：即1个节点(node)至多有2个子节点(child node)。
遍历(traversal)：
分3种：前序遍历（Pre-order traversal）、中序遍历（In-order traversal）、后序遍历（Post-order traversal）。
前序遍历（Pre-order traversal）：拷贝树
顺序为中左右。
中序遍历（In-order traversal）：按序输出
顺序为左中右。
predecessor：在中序排列中一个节点的前一个节点，称为该节点的predecessor，从二叉树图上可以看出是一个节点左子树中最右边的节点。
successor：在中序排列中一个节点的后一个节点，称为该节点的successor，从二叉树图上可以看出是一个节点右子树中最左边的节点。
后序遍历（Post-order traversal）：删除(free)树
顺序为左右中。
实现：使用递归（recursion）
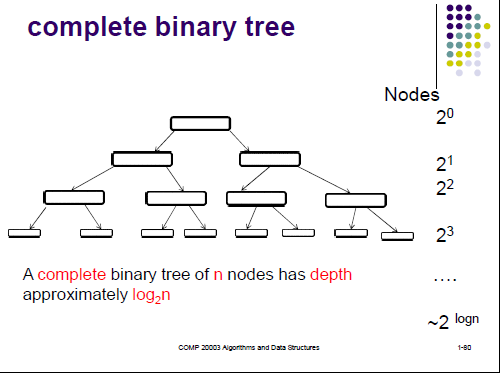
完全二叉树(complete binary tree)：除了最下层，其余层的节点都有2个节点，而最下层的节点只能在最左边的二叉树。
完全二叉树的特性：
n个节点的完全二叉树，它的深度(depth)或高度(height)大约(approximately)是log2n，注意：height和depth均是从0开始计数的。
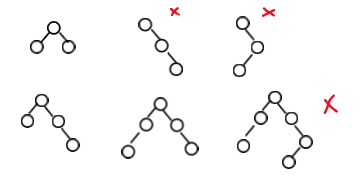
二叉搜索树(binary search tree)：一个节点的值比它左边连结的子节点们的值都大(或等于)，比它右边连接的子节点们都小(或等于)的二叉树，最差情况是插入的值是已经按顺序排好的，此时树变成了stick，实际上成了链表。
AVL树(名字来源于发明者的首字母)：每个节点的左右子树的高度(height)差的绝对值<=1的二叉树，当高度差>1时，则要进行旋转(rotation)操作保持平衡(keep balanced，即所有左右子树的高度差的绝对值<=1)。
保持平衡(keep balanced)：
在每个节点边上写上高度差，从下往上看，从首先看到绝对值大于1的节点进行操作，分为两种情况：
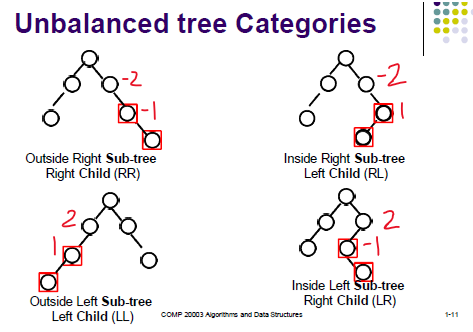
Single Rotation(符号相同)：
LL:Right Rotation
RR:Left Rotation
Double Rotation(符号不同):
RL:先Right Rotation，再Left Rotation
LR:先Left Rotation，再Right Rotation
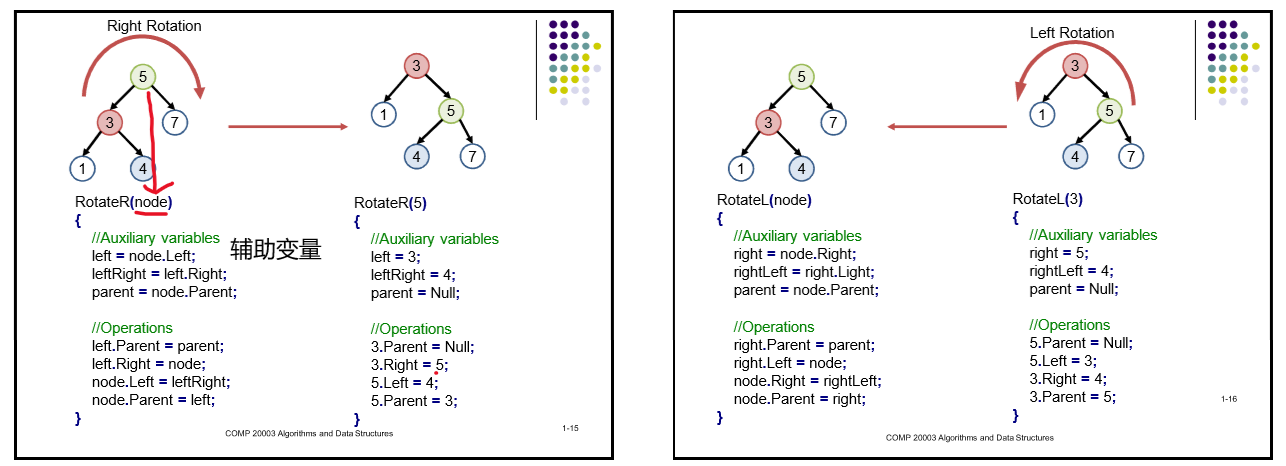
树的旋转(Rotation):
分为左旋钻(Left Rotation)，右旋转(Rigth Rotation)。
节点删除(deletion from bst)：
共2步：1.找到该节点。2.删除该节点。如何找很简单，但找到后删除还要将该节点的叶子接上去（如果有）。删除节点分为3中情况：
1：该节点是叶子节点（无child），直接删除。
2：该节点仅有一个child（左或右），用该child替代。
3：该节点有2个children。
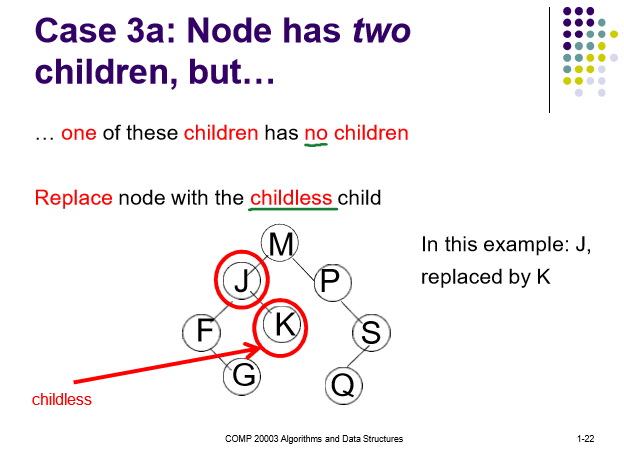
3a:其中一个children没有child，用该节点替代。
3b: 2个children都有child，用中序排列中目标节点的前一个(predecessor)或后一个(successor)替代。
