数字设计--亚稳态
亚稳态
FPGA 等数字设备中的所有寄存器都定义了信号时序要求----允许每个寄存器在其输入端正确捕获数据并产生输出信号。为确保可靠操作,寄存器的输入必须在时钟边沿之前的最短时间(建立时间 setup time 或 \(t_{su}\))和时钟边沿之后的最短时间(保持时间 hold time 或 \(t_H\))保持稳定。然后寄存器输出在指定的时钟到输出延迟 (\(t_{co}\)) 之后可用。如果数据信号转换违反了寄存器的建立时间\(t_{su}\)或保持时间\(t_H\)时序要求,则寄存器的输出可能会进入亚稳态。
在亚稳态中,寄存器输出在高电平和低电平状态之间徘徊一段时间,这意味着输出转换到定义的高电平或低电平状态被延迟,时间将超过指定的\(t_{co}\)。
在同步系统中,输入信号必须始终满足寄存器时序要求,因此一般不会出现亚稳态。(如果同步系统中包含复位信号,同步复位的建立时间和撤离时间不满足寄存器的建立时间和保持时间,就会发生亚稳态,但也只会影响一个时钟,在下一个时钟就会恢复)。
当信号在不相关或异步时钟域的电路之间传输时,通常会出现亚稳态问题。在这种情况下,设计人员不能保证信号将满足\(t_{su}\)或\(t_H\)时序要求,因为信号可以在相对于目标时钟的任何时间到达。
但是,并非每个违反寄存器\(t_{su}\)或\(t_H\)的信号转换都会导致亚稳态输出。
寄存器进入亚稳态的可能性和返回稳定状态所需的时间取决于制造设备所使用的工艺技术和操作条件。在大多数情况下,寄存器会很快恢复到稳定的定义状态。
亚稳态出现的原因
我们在分析元器件时,是把元器件抽象为理想器件以简化分析,但实际的元器件并不是理想的。
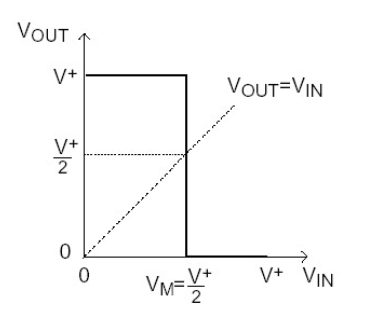
举个例子,我们在分析反相器器件的时候,当输入电压大于\(V_M\)(高电平)时,就认为输出电压为\(0\)(低电平),当输入电压小于\(V_M\)(低电平)时,就认为输出电压为\(V^+\)(高电平)。当然这是理想情况。
实际上器件的特性是这样的
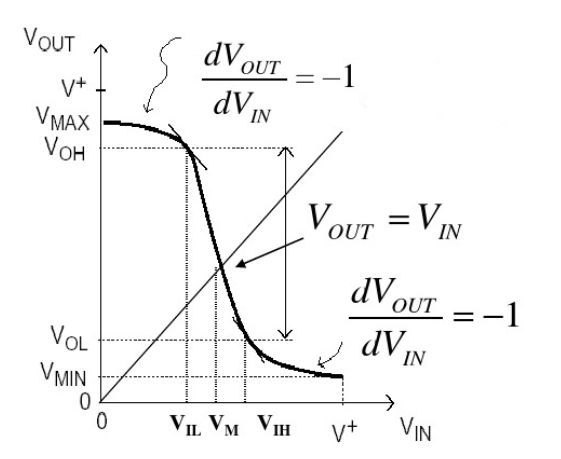
器件的输出电压不是理想的直上直下,他有一个过渡的过程。当输入电压小于\(V_{IL}\),输出电压大于\(V_{OH}\),当输入电压大于\(V_{IH}\),输出电压小于\(V_{OL}\)。当输入电压在\(V_{IL}\)到\(V_{IH}\)范围内,输出电压从\(V_{OH}\)到\(V_{IH}\)范围波动。
我们认为输入电压低于\(V_{IL}\)时为低电平,当输入电压高于\(V_{IH}\)时为高电平,与此相对的输出电压\(V_{OH}\)看作高电平,\(V_{OL}\)看作低电平。
数字化电路都是二值化的,只有0和1,理想情况下,如果输入电压高于\(V_{th}\)那么就是1,如果低于\(V_{th}\)就是0,\(V_{th}\)叫做判断阈值。但是实际情况往往不是这样的,没有一个点来作为分界线,实际的电路做不出来。实际上是高于\(V_H\)才算1, 低于\(V_L\)才算0, \(V_H\)>\(V_L\),也就是说高阈值\(V_H\)和低阈值\(V_L\)之间是有一段距离的。
如果输入电压在\(V_{OH}\)到\(V_{IH}\)之间的范围,那么输出将在\(V_{OL}\)和\(V_{OH}\)范围之内,这是输出既不是高电平又不是低电平,将会导致亚稳态。
当然器件实际上的变化特性与理想有差距是一方面,实际寄存器的结构也会导致亚稳态的产生。
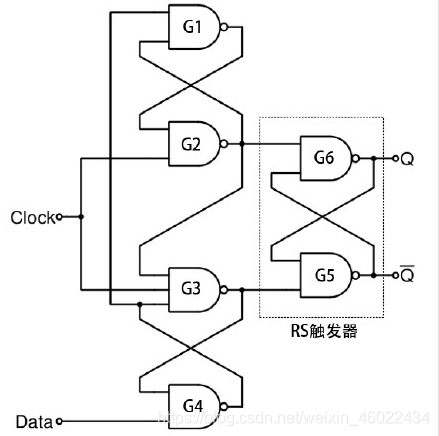
上图是经典上升沿D触发器的内部结构图:
与非门G1到G4是维持阻塞电路,G5和G6构成一个RS触发器用于数据的锁存。
图中可以看到,时钟信号直接作用在了G2和G3上面,也就意味着G2和G3是真正的采样传输门电路,输入信号应该要正确的被G2和G3采样后传输至后面的RS触发器。我们注意到,数据在传输到G3之前经过了G4,传输至G2之前经过了G4和G1。我们知道,实际情况中信号经过门电路是有延迟的。所以输入信号在到达G2和G3之前经过了G1和G4的延迟,因此就引入了建立时间的概念:建立时间就是为了补偿信号在G1和G4上的延迟。也就是数据在时钟沿来临之前,需要足够的建立时间让信号经过G1和G4到达G2和G3。触发器的建立时间主要取决于G1和G4.
那么保持时间呢?一样的,上升沿来临时,数据通过G2和G3传输至后面的RS触发器,但G2和G3也会存在延时。因此又引入了保持时间的概念:保持时间就是为了补偿信号在G2和G3上的延迟。也就是数据在时钟沿来临之后,需要足够的保持时间让信号正确的从G2和G3传输至RS触发器。
当CLK=1时,对于上图中与门G1和G4,G2和G3,此时与门内部MOS门还没有完全关闭(传输门关闭需要时间,时钟刚拉高时还不能阻止输入信号传入)。如果此时输入的信号变化则将会传播到后面的RS触发器,影响RS触发器保存的有效电平状态信号。同时因为时钟沿之后变化的数据其稳定时间没有达到RS触发器的建立时间,同样会引起RS触发器内部的环路震荡,产生亚稳态。
由于触发器的保持时间不仅取决于G1到G4还包含着RS触发器的建立时间,进而可以推断出,一般D触发器的保持时间比建立时间要长。
从上面的分析可以看出,如果不满足寄存器的建立时间和保持时间,一方面寄存器采样的输入电压可能在非触发电压之间,导致寄存器输出电压的不稳定,另一方面即使能够采样到正确的输入电压,但是留给输入信号传递到触发器内部后一级RS触发器的时间不够或者根本不能正确传递到寄存器的RS寄存器部分(在前一级部分传递时输入信号发生变化,导致寄存器震荡或者输入电压达不到触发电压区间),导致最后输出发生亚稳态。
综上,如果不满足寄存器的建立时间和保持时间,输出将会导致亚稳态,但也不是绝对关系,也有可能虽然存在亚稳态,但很快就稳定下来,这时我们就认为没发生亚稳态(?)
当发生亚稳态时,寄存器的输出可能是错误的,寄存器最后最稳定的值是随机的。当寄存器输入的变化越靠近时钟沿,输出稳定的时间越长。
亚稳态的危害
如果数据输出信号在下一个寄存器捕获数据之前解析为有效状态,则亚稳态信号不会对系统操作产生负面影响。但是,如果亚稳态信号在到达下一个设计寄存器之前没有解析为低或高状态,则可能导致亚稳态的传播,可能会使下一级产生亚稳态。
亚稳态这种现象是不可避免的,哪怕是在同步电路中也有概率出现,所以作为设计人员,我们能做的是减少亚稳态发生的概率,当然这也是一个稳健的系统所必须拥有的前提条件。
MTBF
亚稳态导致的平均故障间隔时间或MTBF(Mean Time Between Failure)提供了对亚稳态可能导致设计失败的实例之间的平均时间的估计。更高的 MTBF(例如亚稳态故障之间的数百或数千年)表明设计更稳健。
可以使用有关设计和器件特性的信息来计算特定信号传输或设计中所有传输的亚稳态 MTBF。同步器链的 MTBF 使用以下公式和参数计算:
\(C_1\)和 \(C_2\)常数取决于器件工艺和操作条件。\(f_{CLK}\) 和\(f_{DATA}\)参数取决于设计规范:\(f_{CLK}\)是接收异步信号的时钟域的时钟频率,\(f_{DATA}\)是异步输入数据信号的翻转频率。更快的时钟频率和更快的数据切换会降低(或恶化)MTBF。\(t_{MET}\)参数是可用的亚稳态建立时间,或超出寄存器\(t_{co}\)的可用时序裕量,用于将潜在亚稳态信号解析为已知值(亚稳态稳定所需时间)。同步链的\(t_{MET}\)是链中每个寄存器的输出时序裕量的总和。
如何避免亚稳态
亚稳态是不可避免的,但是我们可以减少亚稳态的发生和传播,从上面的内容中可以,我们有以下减少亚稳态的建议
- 使用同步器;使用同步器可以减少采样异步信号导致的亚稳态。
- 在满足要求的情况下,降低时钟频率。从上面的式子中可以知道,降低时钟频率,可以降低故障的发生率。
- 采用反应更快的触发器。上面的式子中的常数跟触发器有关,如果有更快的触发器,同样可以减少亚稳态的产生。
- 减少使用或者避免使用那种信号翻转时间很长的输入信号,如果翻转时间长,那么进入器件未定义的电平的时间也很长,容易导致亚稳态的产生。
参考
芯片设计进阶之路—亚稳态和同步器 - 知乎 (zhihu.com)
(9条消息) FPGA中亚稳态的理解(Understanding Metastability in FPGAs)_孤独的单刀的博客-CSDN博客
漫谈STA-setup/hold time (qq.com)
亚稳态与多时钟切换 - IC_learner - 博客园 (cnblogs.com)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号