数电基础---原码,反码和补码
一切都会好起来的
主要介绍原码,反码和补码的概念。试着换个角度去看这个“人造”的概念。
原码
我们平时的计数运算都是通过十进制来进行的,对于负数,我们就在十进制数前面加负号,但是对于数字电路来说,平时计算计数都是用二进制来进行的,这就涉及到一个问题那就是如何用二进制来表示负数。
一种方式就是类似于我们对十进制数操作那样,我们在数字的前面加一位表示符号的位,叫符号位,符号位为0表示这个数是正数,符号位为1表示这个数是负数,这种形式的数成为原码。
对于数字电路来说,加法运算我们可以通过加法器来实现,加法器我们可以通过异或门或者组合逻辑来实现,但对于减法器来说实现起来就没有那么简单了,这时我们用原码来运算就比较麻烦了。我们希望能不能用容易实现的加法器来实现数字减法的操作,这里我们就要引入补码的概念。
反码,补码
如何用加法来实现减法?对于正常的数值运算应该是做不到的,因为我们一般操作的时候数值的取值范围是无穷大,但如果说我们做运算的范围是在有限域之中,那情况就不一样了。
举个例子,对于一个有限域,他的数值域中是进行模12的操作,那么
通过有限域内取模的操作我们可以将\(10-5\)的问题转化为\(10+7\)的形式,将减法转换成了加法操作,我们就称\(7\)是对模\(12\)的补数,也称作为补码(Complement)。
而对于数字运算来说,有限位的二进制运算也可以看作有限域,比如对于4位二进制加减运算,他的结果是有限的,只有16种可能的结果,我们就可以将减法运算通过有限维二进制隐含的取模操作来进行。
举个例子,在不考虑符号位的情况下,
如果不再用减法器,只用加法器的情况下,舍弃最高位的进位,则可以用
因为四位二进制数的进位基数是\(16(10000)\),所以\(1001(9)\)恰好是\(0111(7)\)对模\(16\)的补码。
从数学方面的角度,不包括符号位,只考虑数据位,对于有效数字位\(n\)位的二级制数\(N\),它的补码\((N)_{COMP}\)可以表示为
即正数(当符号位为0时)的补码与原码相同,负数(当符号位为1时)的补码等于\(2^n - N\)。注意大括号中参与其中运算的只有数值部分,而条件中\(N\)为负数,则包含符号位(要不哪来的负数之说)。如果考虑符号位,符号位保持不变。
为了避免在求补码的过程中做减法运算,通常时先求出\(N\)的反码\((N)_{INV}\),然后在负数的反码上加一得到补码。
二进制\(N\)的反码\((N)_{INV}\)是这样定义的
当\(N\)为负数时,\(N+(N)_{INV}=2^n-1\),\(n\)位全为\(1\)的二进制数表示\(2^n-1\)的十进制数,则\((N)_{INV}\)表示将二进制数按位取反的结果(因为加上按位取反,则每一位上全都是),在二进制电路中,取反操作是很容易实现的。
当\(N\)为负数时,\((N)_{INV}+1=2^n-N\),\((N)_{COMP}=2^n-N\),所以可以得到
即二进制负数的补码为他的反码加一,即除了符号位,按位取反再加一。
关于符号位,为什么符号位不参与求补码的运算呢?
由前面的数学定义,参与运算的只有运算数的数值部分,符号是包含在条件之中的,那为什么符号数要保持不变,有会不会对运算产生影响呢
我个人的看法,首先对于一个数,我们要知道他是正是负,所以需要符号位,在运算的时候,符号位相当于后面数值位的进位。
举个例子:
首先我们看一下四位二进制的原码补码表:
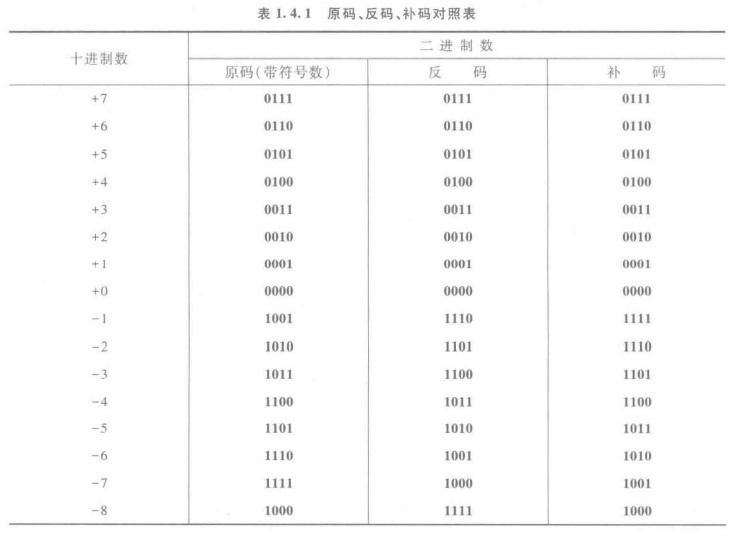
从图上我们可以看到,当负数比较小时,后面数值位上的数值比较大,当负数比较大时,后面数值位上的数值比较小。

结合上面两个图,当13加上-10时,-10负数比较小,所以他的数值位数值比较大,和13的数值位相加会产生进位,进位和-10的符号位相加,符号位变成0,当-13加上10时,-13负数比较大,所以他的数值位数值比较小,和10的数值相加不会产生进位,所以最后的符号位还是1,如何让定义数值的大小,还拿10举例子,当相加的数是-10时,最后的结果是0,当相加数大于-10,数值位比较小,则数值位相加不会产生进位,当相加数小于-10时,数值位比较大,则数值位相加会产生进位。
需要注意的是,两个同符号数相加时,它们的绝对值之和不能超过有效数字位所能表示的最大值,否则则会得出错误的计算结果,因为数值位相加产生了进位,影响到了符号位。


