有关连通性的状压 DP: 插头 DP
插头 DP (Plug Dynamic Programming)
陈丹琦在 2008 年引入国内 OI 界的插头 DP 是用来解决一些和连通性有关的问题的状态压缩算法. 一般采用轮廓线的方式逐格转移.
经典问题是给一张有障碍的棋盘, 求有多少条不同的回路可以覆盖所有无障碍的格点.
状态
显然我们如果仅维护插头存在性, 那么下面这两种情况就成了同一种状态.
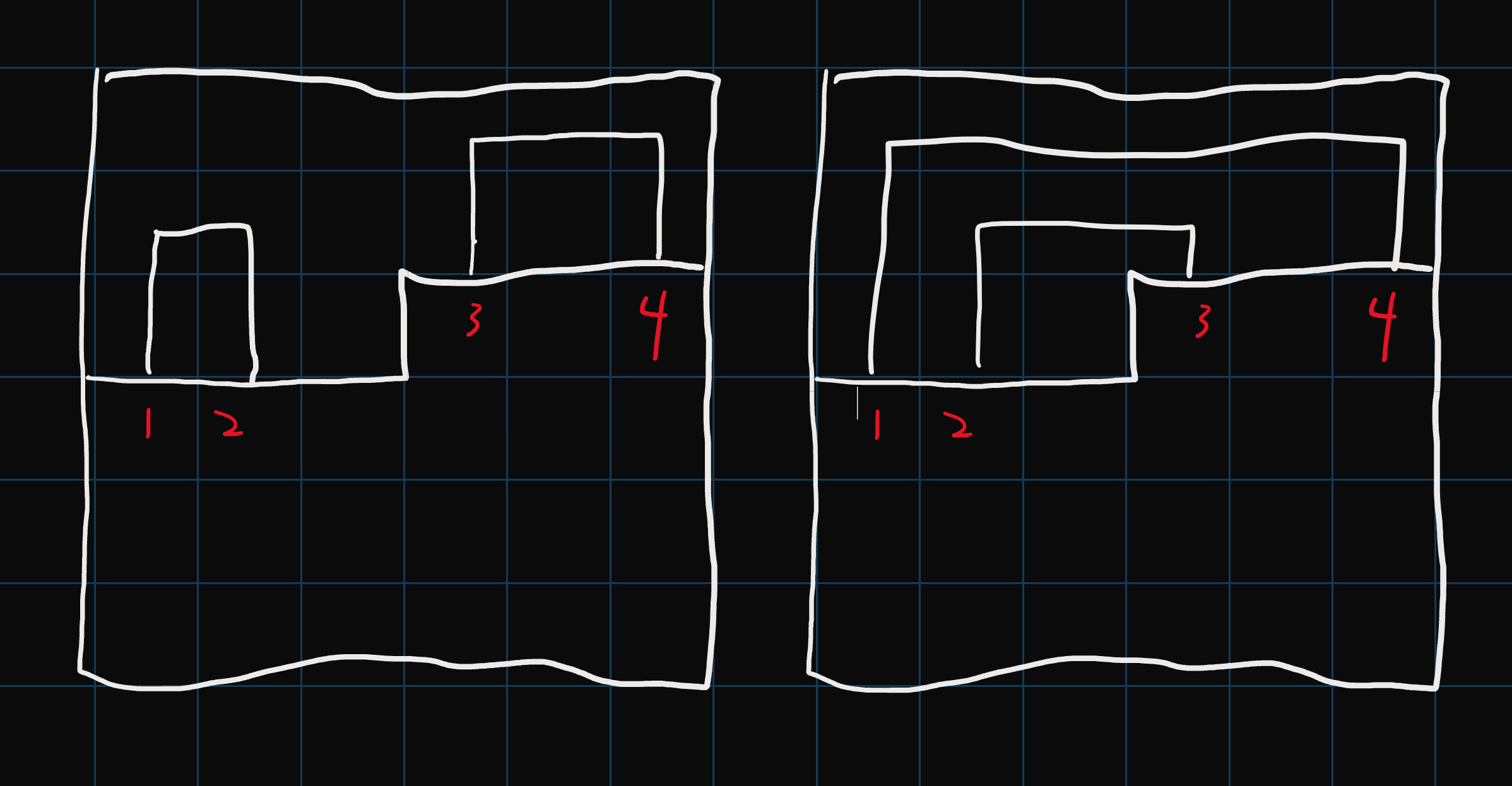
我们不希望第一种情况中的 \(3\) 和 \(4\) 的插头被连起来, 但是允许第二种情况中 \(3\) 和 \(4\) 的插头被连起来. 所以我们需要维护轮廓线上每个插头的连通性.
可以用最小表示法表示每个插头所在的连通块. 用一个 \(\lfloor \frac 1m \rfloor\) 进制数表示轮廓线的状态. 每一位表示轮廓线上每个位置的状态, 这一位是 \(0\) 表示这个位置没有插头, 否则表示这是轮廓线上出现的第几个插头所属的连通块. 通过预处理处理出合法状态集合再进行转移.
还有一个方法是把每一个插头看作是括号, 上括号和下括号作为一个连通块在轮廓线上的两端. 我们用一个三进制数表示状态. \(0\) 表示此位置无插头, \(1\) 表示此位置为上括号插头, \(2\) 表示为下括号插头.
转移
实践证明括号表示法在各方面都比较优秀, 接下来考虑如何转移.
我们每次转移有三种可能的结果:
- 连接两个连通块
- 新建一个连通块
- 延伸一个连通块
分别对应了转移的格子有 \(2\) 个插头相邻, 有 \(0\) 个插头相邻, 有 \(1\) 个插头相邻的情况.
对于没有插头相邻的情况, 我们只有一种转移, 就是使这个格子的右边和下面都存在插头, 变成一个新的连通块.
对于有两个插头相邻的情况, 我们需要进行选择, 转移还是不转移. 如果两个插头都是上括号或都是下括号, 可以转移, 这会连接两个连通块, 需要某个插头的另一半改变自己的类型. 这就需要预处理每个状态中插头的另一半的位置. 如果左边的插头是下括号, 右边插头是上括号, 也是可以转移的, 且不需要改变别的括号类型. 左边的插头是上括号, 右边插头是下括号的情况是不可以转移的, 这会使得一个连通块被闭合. 这个状态只能在最后一个无障碍的格子才能被转移.
对于只有一个插头相邻的情况, 这个格子的一端肯定需要连接这个插头, 另一端可以在右边或下边随意找一个位置作为自己的第二个插头, 这个插头类型继承自己相邻的格子的插头类型.
因为位运算的效率高于取余, 所以一般用 \(4\) 进制数表示 \(3\) 进制的状态.
代码实现
DFS 求出可行的状态, 给每个状态编号, 我们用哈希表把状态映射到编号. (我甚至可以滚动数组)
More details are in the code.
unordered_map<unsigned, unsigned> List;
unsigned long long f[42005], Tmp[42005];
unsigned g[42005][13], Find[42005], Stack[13], STop(0), Con(0), Now(0);
unsigned A, B, C, D, t, m, n, N;
unsigned Cnt(0), Ans(0);
char a[13][13], Flg(0);
inline void Nxt(unsigned& x, unsigned& y) {
if (y + 1 >= m) ++x, y = 0; else ++y;
}
inline void Lst(unsigned& x, unsigned& y) {
if (y) --y; else --x, y = m - 1;
}
inline void DFS(unsigned Dep) {
if(Dep > m) {
if(!Cnt) {
List[Now] = ++Con, Find[Con] = Now;
for (unsigned i(0), j(0); i <= m; ++i, j += 2) {
char Cur((Now >> j) & 3);
if(Cur) {
if(Cur == 1) Stack[++STop] = i;
else g[Con][Stack[STop]] = i, g[Con][i] = Stack[STop--];
}
}
}
return;
}
DFS(Dep + 1);
Now ^= (1 << (Dep << 1)), ++Cnt;
DFS(Dep + 1);
--Cnt, Now ^= (1 << (Dep << 1));
if(Cnt) {
Now ^= (2 << (Dep << 1)), --Cnt;
DFS(Dep + 1);
++Cnt, Now ^= (2 << (Dep << 1));
}
}
signed main() {
n = RD(), N = ((1 << (m = RD()) + 1) << 1), DFS(0);
for (unsigned i(1); i <= n; ++i) scanf("%s", a[i]);
for (unsigned i(1); (i <= n) && (!Flg); ++i) for (unsigned j(0); j < m; ++j)
if (a[i][j] ^ '*') { Flg = 1, A = i, B = j;break; }
if (!Flg) { printf("1\n"); return 0; } Flg = 0;
for (unsigned i(n); i && (!Flg); --i) for (unsigned j(m - 1); ~j; --j)
if (a[i][j] ^ '*') { Flg = 1, C = i, D = j;break; }
if ((B == (m - 1)) || (!D)) { printf("0\n"); return 0;}
Lst(A, B), f[1] = 1;
unsigned Pli(A), Plj(B); Nxt(Pli, Plj), Lst(C, D);
for (unsigned i(A), j(B); (i ^ C) || (j ^ D); i = Pli, j = Plj, Nxt(Pli, Plj)) {
if(a[Pli][Plj] ^ '.') {
if(Plj) {for (unsigned k(1); k <= Con; ++k) if (f[k]) {
unsigned Cur(Find[k]), Up(Cur & (3 << ((Plj + 1) << 1))), Lef(Cur & (3 << ((Plj << 1))));
if(!(Up | Lef)) Tmp[List[(Cur ^ Up) ^ Lef]] += f[k];
}}
else for (unsigned k(1); k <= Con; ++k) if (f[k]) {
unsigned Cur(Find[k]);
if(!(Cur & 3)) Tmp[List[Cur << 2]] += f[k];
}
memcpy(f, Tmp, (Con + 1) << 3);
memset(Tmp, 0, (Con + 1) << 3);
continue;
}
if(!Plj) {
for (unsigned k(1); k <= Con; ++k) if (f[k]) {
unsigned Cur(Find[k]), To(Cur << 2);
char Up(Cur & 3);
if (Up) Tmp[List[To]] += f[k], To ^= 5;
else To ^= 9;
Tmp[List[To]] += f[k];
}
} else for (unsigned k(1); k <= Con; ++k) if (f[k]) {
unsigned Cur(Find[k]), To(Cur);
char Up((Cur >> ((Plj + 1) << 1)) & 3), Lef(Cur >> ((Plj << 1)) & 3);
if(!(Up | Lef)) To ^= (9 << (Plj << 1));
else if(a[Pli][Plj]) {
if((!Lef) || (!Up)) Tmp[k] += f[k], To ^= (((Up + Lef) | ((Lef + Up) << 2)) << (Plj << 1));
else {
To ^= (Up << ((Plj + 1) << 1));
To ^= (Lef << (Plj << 1));
if(Lef & Up) To ^= (3 << (g[k][Plj + (Lef == 1)] << 1));
else if(Lef == 1) continue;
}
}
Tmp[List[To]] += f[k];
}
memcpy(f, Tmp, (Con + 1) << 3);
memset(Tmp, 0, (Con + 1) << 3);
}
Nxt(C, D), Ans = ((1 << (D << 1)) | (2 << ((D + 1) << 1)));
printf("%llu\n", f[List[Ans]]);
return Wild_Donkey;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号