ZROI Day11-Day20 笔记
ZROI
Day11: SA
倍增
过水已隐藏
SA 做 SAM 板子
求字符串本质不同的子串个数.
所有字串都可以唯一地表示为第 i 个后缀的第 j 个前缀, 共 n(n+1)2 个. 所以我们只要排序后缀, 然后求出 LCP_{i, i + 1}, 就可以知道一个后缀和相邻后缀有多少前缀相同, 总数减去重复的数量就是不同的数量.
例题
求所有无序后缀对两两 lcp 之和.
定义 hi=lcpi,i+1. 有一个引理: lcpi,j=min(hk)k∈[i,j).
单调栈求出 hi 左边的连续大于等于它的数量 li, 右边连续大于它的数量 ri, 这时统计 n∑i=1(ri+li+1)×hi.
CF1073G
给一个字符串, 每次询问给两个数集 A, B, 求 A 中每个后缀和 B 中每个后缀的 LCP 长度之和.
所有询问 A 或 B 大小之和不超过 2∗105.
首先想到暴力, 可以每次枚举所有数对, 在后缀树上两两求 LCA, 将 Len 统计入答案.
然后用树链剖分优化, 因为一个 LCA 的 Len 是它到根上的所有点的 Len 和父亲的 Len 的差的总和. 可以用树链剖分维护这个差加权的区间和. 对于每个 A 集合的点, 将它到根的所有点的权值加 1. 然后查询每个 B 集合的点到根的加权的差的和, 即可在 O(n+log2n(∑|A|+∑|B|)) 的时间内求出答案.
也可以用虚树, 这样可以在 O(n+logn(∑|A|+∑|B|)) 内求出答案.
还有后缀数组的做法, 先求后缀数组, 然后求出 Height, 数组, 存入 ST 表中.
对于朴素的做法, 枚举所有 A, B 中的元素, 查询其区间 Height 最小值, 复杂度 O(nlogn+|A|∗|B|), 尝试将 A, B, 按 RK 排序, 这样可以先处理 RKAi≤RKBj 的情况, 然后处理 RKBi<RKAj 的情况.
对于 RKAi≤RKBj, 双指针扫描两个数组, 对于一个 Bj, 将所有可能对它有贡献的 Ai 的 RKBjmink=RKAi+1Heightk 插入权值线段树中, 统计答案.
特殊地, 对于 Ai=Bj, 将 n−Ai+1 插入线段树.
考虑由 Bj 到 Bj+1 变化后, 线段树中的值对答案的贡献变化, 发现
所以只要每次移动 j 的时候把线段树中比 RKBj+1mink=RKBj+1Heightk 大的值都变成 RKBj+1mink=RKBj+1Heightk 就可以了.
RKBi<RKAj 的情况也和前面所说的相似.
所以需要支持区间删除, 单点修改, 全局查询, 复杂度 O((n+|A|+|B|)logn).
unsigned ScdRk[200005], Bucket[200005], SA[200005], RK[200005];
unsigned RkTmp[400005], ST[18][200005], m, n;
unsigned SzA, SzB, A[200005], B[200005], C, D;
unsigned Bin[20], Log[200005];
unsigned long long Ans(0);
char a[200005];
struct Node {
Node* LS, * RS;
unsigned long long Sum, Cnt;
void Udt() {
this->Sum = this->LS->Sum + this->RS->Sum;
this->Cnt = this->LS->Cnt + this->RS->Cnt;
}
void PsDw() { if (!this->Cnt) this->LS->Cnt = this->RS->Cnt = this->LS->Sum = this->RS->Sum = 0; }
void Add(unsigned L, unsigned R) {
if (L == R) {
(this->Cnt) += D;
this->Sum = this->Cnt * L;
return;
}
this->PsDw();
register unsigned Mid((L + R) >> 1);
if (C <= Mid) { this->LS->Add(L, Mid); }
else { this->RS->Add(Mid + 1, R); }
this->Udt();
}
void QryDel(unsigned L, unsigned R) {
if (L > C) {
D += this->Cnt;
this->Cnt = this->Sum = 0;
return;
}
this->PsDw();
register unsigned Mid((L + R) >> 1);
if (Mid > C) this->LS->QryDel(L, Mid);
this->RS->QryDel(Mid + 1, R);
}
}N[400005], * CntN(N);
void Build(Node* x, unsigned L, unsigned R) {
if (L == R) { return; }
register unsigned Mid((L + R) >> 1);
Build(x->LS = ++CntN, L, Mid);
Build(x->RS = ++CntN, Mid + 1, R);
}
inline unsigned Min(unsigned L, unsigned R) {
register unsigned LenLog(Log[R - L + 1]);
return min(ST[LenLog][L], ST[LenLog][R - Bin[LenLog] + 1]);
}
signed main() {
n = RD(), m = RD();
scanf("%s", a + 1);
for (register unsigned i(1); i <= n; ++i)
++Bucket[RK[i] = (a[i] - 'a' + 2)];
for (register unsigned i(1); i <= 27; ++i)
Bucket[i] += Bucket[i - 1];
for (register unsigned i(1); i <= n; ++i)
SA[Bucket[RK[i]]--] = i;
for (register unsigned i(1), BucketTop(27); i <= n; i <<= 1) {
for (register unsigned j(n - i + 1); j <= n; ++j) ScdRk[j] = j;
for (register unsigned j(1), Top(n - i + 1); j <= n; ++j)
if (SA[j] > i) ScdRk[--Top] = SA[j] - i;
memset(Bucket, 0, (BucketTop + 1) << 2);
for (register unsigned j(1); j <= n; ++j)
++Bucket[RK[j]];
for (register unsigned j(1); j <= BucketTop; ++j)
Bucket[j] += Bucket[j - 1];
for (register unsigned j(1); j <= n; ++j)
SA[Bucket[RK[ScdRk[j]]]--] = ScdRk[j];
BucketTop = 0;
memcpy(RkTmp, RK, (n + 1) << 2);
for (register unsigned j(1); j <= n; ++j)
RK[SA[j]] = ((RkTmp[SA[j]] ^ RkTmp[SA[j - 1]]) || (RkTmp[SA[j] + i] ^ RkTmp[SA[j - 1] + i])) ? (++BucketTop) : BucketTop;
if (BucketTop == n) break;
}
for (register unsigned i(1), j, H(1); i <= n; ++i) {
if (RK[i] == 1) { ST[0][RK[i]] = 0; continue; }
j = SA[RK[i] - 1];if (H) --H;
while ((a[i + H] == a[j + H]) && (i + H <= n) && (j + H <= n)) ++H;
ST[0][RK[i]] = H;
}
for (register unsigned i(1), j(0); i <= n; i <<= 1, ++j)
Bin[j] = i, Log[i] = j;
for (register unsigned i(1); i <= n; ++i)
Log[i] = max(Log[i], Log[i - 1]);
for (register unsigned i(1), j(0); i <= n; i <<= 1, ++j)
for (register unsigned k(1); k + (i << 1) <= n + 1; ++k)
ST[j + 1][k] = min(ST[j][k], ST[j][k + i]);
B[0] = -1, A[0] = -1, Build(N, 0, n);
for (register unsigned i(1); i <= m; ++i) {
SzA = RD(), SzB = RD(), Ans = 0;
for (register unsigned i(1); i <= SzA; ++i) A[i] = RK[RD()];
for (register unsigned i(1); i <= SzB; ++i) B[i] = RK[RD()];
sort(A + 1, A + SzA + 1), sort(B + 1, B + SzB + 1);
for (register unsigned i(1), j(1); j <= SzB; ++j) {
C = Min(B[j - 1] + 1, B[j]), D = 0, N->QryDel(0, n), N->Add(0, n);
while ((A[i] <= B[j]) && (i <= SzA)) {
C = ((A[i] ^ B[j]) ? (Min(A[i] + 1, B[j])) : (n - SA[A[i]] + 1)), D = 1, N->Add(0, n);
++i;
}
Ans += N->Sum;
}
C = 0, N->QryDel(0, n);
for (register unsigned i(1), j(1); j <= SzA; ++j) {
C = Min(A[j - 1] + 1, A[j]), D = 0, N->QryDel(0, n), N->Add(0, n);
while ((B[i] < A[j]) && (i <= SzB)) {
C = Min(B[i] + 1, A[j]), D = 1, N->Add(0, n);
++i;
}
Ans += N->Sum;
}
printf("%llu\n", Ans);
}
return Wild_Donkey;
}
CF666E
一个母串 S, n 个模式串 Ti, 每次询问子串 S[l1,r1] 在 Tii∈[l2,r2] 中哪个模式串中出现最多.
因为今天是 SA 场, 所以感觉还是先介绍 SAM 做法比较礼貌.
首先建立 GSAM, 将离线下来的询问的子串对应的节点打上标记, 那么它会在它后缀树上子树上的所有节点代表的字符串中出现, 后缀树上每个点建线段树存储所属的字符串编号, 然后从下到上合并线段树, 每次遇到有标记的节点, 区间查询最大值即可.
好了这就是又简单又无脑的 SAM 做法, 接下来看恐怖的又难写又难想而且慢的 SA 做法.
将所有模式串加入 S 后面, 中间插特殊字符, 然后求 SA, h.
离线所有询问, 将每个询问转化为求对于 x∈[Headl2,Tailr2] 区间 LCPl1,x≥r1−l1+1 的 x 数量. 而 LCPl1,x≥r1−l1+1 的 Rank 一定是一段连续的区间, 并且可以二分, 然后用莫队维护在每个区间 [Headl2,Tailr2] 中所有 Rank 在对应区间中的 x 属于每个模式串的数量 Cnt.
因为区间众数带一个值域约束, 所以对值域分块,
这样就能 O(LenlogLen+q(√Len+√n)) 解决问题了.
真的不懂, 明明可以 logLen 过得轻松写意, 非要 √Len 把 6s 的题跑出 5.35s 的惊心动魄.
unsigned ST[20][600005], Bin[20], Log[600005], ScdRk[600005];
unsigned Bucket[600005], SA[600005], RK[600005], RkTmp[1200005];
unsigned a[50005], BNum[600005], Cnt[50005], AnsN[500005], AnsC[500005];
unsigned m, n, q, A, B, C, D, t, Tmp(0), BlcL, BlcL2;
unsigned AnsBuc[230], BlcCnt[230][50005];
char S[600005];
struct Qry {
unsigned L, R, RL, RR, Bl, Num;
inline const char operator< (const Qry& x) const { return (this->Bl ^ x.Bl) ? (this->Bl < x.Bl) : (this->L < x.L); }
}Q[500005];
inline unsigned Min(unsigned L, unsigned R) {
register unsigned LenLog(Log[R - L + 1]);
return min(ST[LenLog][L], ST[LenLog][R - Bin[LenLog] + 1]);
}
inline void Add(unsigned x) {
if (!x) return;
register unsigned BlcN(x / BlcL2);
--BlcCnt[BlcN][Cnt[x]];
if (++Cnt[x] > AnsBuc[BlcN]) ++AnsBuc[BlcN];
++BlcCnt[BlcN][Cnt[x]];
}
inline void Del(unsigned x) {
if (!x) return;
register unsigned BlcN(x / BlcL2);
--BlcCnt[BlcN][Cnt[x]];
if (!BlcCnt[BlcN][Cnt[x]]) if ((Cnt[x]) == AnsBuc[BlcN]) --AnsBuc[BlcN];
++BlcCnt[BlcN][--Cnt[x]];
}
signed main() {
a[0] = 1;
scanf("%s", S + 1), a[1] = strlen(S + 1) + 1;
n = RD();
for (register unsigned i(1); i <= n; ++i) {
S[a[i]] = '`';
scanf("%s", S + a[i] + 1);
a[i + 1] = a[i] + strlen(S + a[i] + 1) + 1;
}
m = a[n + 1] - 1, BlcL2 = sqrt(n) + 1;
for (register unsigned i(1); i <= m; ++i) ++Bucket[RK[i] = (S[i] -= '_')];
for (register unsigned i(1); i <= 27; ++i) Bucket[i] += Bucket[i - 1];
for (register unsigned i(1); i <= m; ++i) SA[Bucket[RK[i]]--] = i;
for (register unsigned i(1), BucketSize(27); i <= m; ++i) {
memset(Bucket, 0, (BucketSize + 1) << 2);
for (register unsigned j(1); j <= m; ++j) ++Bucket[RK[j]];
for (register unsigned j(1); j <= BucketSize; ++j) Bucket[j] += Bucket[j - 1];
for (register unsigned j(m - i + 1); j <= m; ++j) ScdRk[j] = j;
for (register unsigned j(1), TopSR(m - i + 1); j <= m; ++j) if (SA[j] > i) ScdRk[--TopSR] = SA[j] - i;
for (register unsigned j(1); j <= m; ++j) SA[Bucket[RK[ScdRk[j]]]--] = ScdRk[j];
memcpy(RkTmp, RK, (m + 1) << 2), BucketSize = 0;
for (register unsigned j(1); j <= m; ++j) RK[SA[j]] = ((RkTmp[SA[j]] ^ RkTmp[SA[j - 1]]) || (RkTmp[SA[j] + i] ^ RkTmp[SA[j - 1] + i])) ? (++BucketSize) : (BucketSize);
if (BucketSize == m) break;
}
for (register unsigned i(0); i <= n; ++i)
for (register unsigned j(a[i]); j < a[i + 1]; ++j) BNum[RK[j]] = i;
for (register unsigned i(1), j(0); i <= m; ++i) {
if (j) --j;
if (RK[i] == 1) { ST[0][RK[i]] = 0; continue; }
while ((SA[RK[i] - 1] + j <= m) && (i + j <= m) && (S[i + j] == S[SA[RK[i] - 1] + j])) ++j;
ST[0][RK[i]] = j;
}
for (register unsigned i(1), j(0); i <= m; i <<= 1, ++j)
for (register unsigned k(1); k + (i << 1) - 1 <= m; ++k)
ST[j + 1][k] = min(ST[j][k], ST[j][k + i]);
for (register unsigned i(1), j(0); i <= m; i <<= 1, ++j) Bin[j] = i, Log[i] = j;
for (register unsigned i(1); i <= m; ++i) Log[i] = max(Log[i], Log[i - 1]);
q = RD(), BlcL = (m / sqrt(q)) + 1;
for (register unsigned i(1); i <= q; ++i) {
Q[i].RL = RD(), Q[i].RR = RD(), A = RD(), B = RD() - A + 1, A = RK[A], Q[i].Num = i;
register unsigned BL(2), BR(A), BMid;
while (BL < BR) {
BMid = (BL + BR) >> 1;
if (Min(BMid, A) >= B) BR = BMid;
else BL = BMid + 1;
}
Q[i].L = (ST[0][BL] < B) ? BL : (BL - 1), BL = A + 1, BR = m;
while (BL < BR) {
BMid = (BL + BR + 1) >> 1;
if (Min(A + 1, BMid) >= B) BL = BMid;
else BR = BMid - 1;
}
Q[i].R = (ST[0][BL] < B) ? (BL - 1) : BL;
}
for (register unsigned i(1); i <= n; ++i) Q[i].Bl = Q[i].R / BlcL;
sort(Q + 1, Q + q + 1);
for (register unsigned i(1), NowL(1), NowR(0), TmpAns, TmpPos, LBlc, RBlc, TmpL, TmpR; i <= q; ++i) {
while (NowL > Q[i].L) Add(BNum[--NowL]);
while (NowR < Q[i].R) Add(BNum[++NowR]);
while (NowL < Q[i].L) Del(BNum[NowL++]);
while (NowR > Q[i].R) Del(BNum[NowR--]);
LBlc = (Q[i].RL + BlcL2 - 1) / BlcL2, RBlc = (Q[i].RR + 1) / BlcL2, TmpAns = TmpPos = 0;
if (RBlc <= LBlc) {
for (register unsigned j(Q[i].RR); j >= Q[i].RL; --j) if (Cnt[j] >= TmpAns) TmpAns = Cnt[j], TmpPos = j;
AnsC[Q[i].Num] = TmpAns, AnsN[Q[i].Num] = TmpPos; continue;
}
for (register unsigned j(RBlc - 1); j >= LBlc; --j) if (AnsBuc[j] >= TmpAns) TmpAns = AnsBuc[j], TmpPos = j;
TmpL = TmpPos * BlcL2, TmpR = (TmpPos + 1) * BlcL2;
for (register unsigned j(TmpL); j < TmpR; ++j) if (Cnt[j] == TmpAns) { TmpPos = j; break; }
for (register unsigned j((LBlc* BlcL2) - 1); j >= Q[i].RL; --j) if (Cnt[j] >= TmpAns) TmpAns = Cnt[j], TmpPos = j;
for (register unsigned j((RBlc* BlcL2)); j <= Q[i].RR; ++j) if (Cnt[j] > TmpAns) TmpAns = Cnt[j], TmpPos = j;
AnsC[Q[i].Num] = TmpAns, AnsN[Q[i].Num] = TmpPos;
}
for (register unsigned i(1); i <= q; ++i) printf("%u %u\n", AnsN[i], AnsC[i]);
return Wild_Donkey;
}
CF1063F
将字符串 S 划分成 m 个不相交的子串 Ti, 使得从左到右排序后 Ti 是 Ti−1 的严格子串 (不是它本身的子串), 求这个最大的 m.
容易发现一个显然的性质: LenTi=LenTi+1+1 一定不会使答案更劣.
所以 m 是 √n 规模的.
设 fi 表示以 Si 开头的子串作为 T1, m 的最大值. 可以发现 fi≤fi+1+1, 这是因为如果 fi=fi+1+2, 那么将 fi 方案中的所有子串 T 都删掉一个字符, 得到了 fi+1+1 个子串也是合法的, 所以这时 fi+1 应该是原来的 fi+1+1.
于是可以发现在 fi−1 确定的情况下, fi 有 fi−1+1 种可能的取值, 即自然数 [1,fi−1+1].
我们只要二分所有可能的取值 x, 然后判断满足 j≥i+x 的 LCPi,j≥x−1 的 j 是否满足 fj≥x−1 即可.
发现完全没必要二分, 因为每个 fi 最多比 fi+1 大 1, 所以即使倒序枚举所有 x, 也不过是均摊 O(n) 次判断而已.
对于判断, 如果直接枚举是 O(n) 的,尝试优化.
发现对 j 的约束 j>=i+x, 因为是倒序枚举 x, 并且随着 i 的减小, x 最多增加 1, 所以每次判断时 i+x 是单调不增的.
利用这个性质, 我们可以每次移动 i+x 之前, 将 i+x 的 f 值插入线段树的 RKi+x 位置中. 然后二分出 LCPi,j>=x−1 的区间, 在线段树上区间查询最大值, 判断这个最大值即可, 每次判断 O(logn).
所以总复杂度是 O(nlogn).
unsigned SA[500005], RK[500005], ScdRk[500005], Bucket[500005], RkTmp[1000005];
unsigned ST[20][500005], Bin[20], Log[500005], f[500005];
unsigned m, n, Cnt(0), A, B, C, D, t, Ans(0), Final(1), Tmp(0);
char aP[500010], * a(aP);
unsigned Min(const unsigned L, const unsigned R) {
unsigned LenLog(Log[R - L + 1]);
return min(ST[LenLog][L], ST[LenLog][R - Bin[LenLog] + 1]);
}
struct Node {
Node* LS, * RS;
unsigned Val;
void Add(unsigned L, unsigned R) {
if (L == R) { this->Val = B;return; }
unsigned Mid((L + R) >> 1);
if (A <= Mid) this->LS->Add(L, Mid);
else this->RS->Add(Mid + 1, R);
this->Val = max(this->LS->Val, this->RS->Val);
}
void Qry(unsigned L, unsigned R) {
if ((A <= L) && (R <= B)) { Ans = max(Ans, this->Val); return; }
unsigned Mid((L + R) >> 1);
if (A <= Mid) this->LS->Qry(L, Mid);
if (Mid < B) this->RS->Qry(Mid + 1, R);
}
}N[1000005], * CntN(N);
void Build(Node* x, unsigned L, unsigned R) {
if (L == R) { return; }
unsigned Mid((L + R) >> 1);
Build(x->LS = (++CntN), L, Mid), Build(x->RS = (++CntN), Mid + 1, R);
}
signed main() {
n = RD();
fread(aP + 1, 1, n + 5, stdin), Build(N, 1, n);
while (a[1] < 'a') ++a;
for (unsigned i(1); i <= n; ++i) ++Bucket[RK[i] = (a[i] -= '`')];
for (unsigned i(1); i <= 26; ++i) Bucket[i] += Bucket[i - 1];
for (unsigned i(1); i <= n; ++i) SA[Bucket[RK[i]]--] = i;
for (unsigned i(1), BucketSize(26); i <= n; i <<= 1) {
memset(Bucket, 0, (BucketSize + 1) << 2);
for (unsigned j(1); j <= n; ++j) ++Bucket[RK[j]];
for (unsigned j(1); j <= BucketSize; ++j) Bucket[j] += Bucket[j - 1];
for (unsigned j(n - i + 1); j <= n; ++j) ScdRk[j] = j;
for (unsigned j(1), TopSR(n - i + 1); j <= n; ++j) if (SA[j] > i) ScdRk[--TopSR] = SA[j] - i;
for (unsigned j(1); j <= n; ++j) SA[Bucket[RK[ScdRk[j]]]--] = ScdRk[j];
memcpy(RkTmp, RK, (n + 1) << 2), BucketSize = 0;
for (unsigned j(1); j <= n; ++j) RK[SA[j]] = ((RkTmp[SA[j]] ^ RkTmp[SA[j - 1]]) || (RkTmp[SA[j] + i] ^ RkTmp[SA[j - 1] + i])) ? (++BucketSize) : (BucketSize);
if (BucketSize == n) break;
}
for (unsigned i(1), j(0); i <= n; ++i) {
if (RK[i] == 1) ST[0][1] = 0;
if (j) --j;
while (a[i + j] == a[SA[RK[i] - 1] + j]) ++j;
ST[0][RK[i]] = j;
}
for (unsigned i(1), j(0); i <= n; i <<= 1, ++j)
for (unsigned k(1); k + (i << 1) - 1 <= n; ++k)
ST[j + 1][k] = min(ST[j][k], ST[j][k + i]);
for (unsigned i(1), j(0); i <= n; i <<= 1, ++j) Bin[j] = i, Log[i] = j;
for (unsigned i(1); i <= n; ++i) Log[i] = max(Log[i], Log[i - 1]);
for (unsigned i(n), j(0), Right(n + 1); i; --i, ++j) {
while (j) {
unsigned BL(1), BR(RK[i]), BMid;
while (BL < BR) {
BMid = (BL + BR) >> 1;
if (Min(BMid, RK[i]) >= j) BR = BMid;
else BL = BMid + 1;
}
A = (ST[0][BL] >= j) ? (BL - 1) : (BL), BL = RK[i] + 1, BR = n;
while (BL < BR) {
BMid = (BL + BR + 1) >> 1;
if (Min(RK[i] + 1, BMid) >= j) BL = BMid;
else BR = BMid - 1;
}
B = (ST[0][BL] >= j) ? (BL) : (BL - 1);
Ans = 0, N->Qry(1, n);
if (Ans >= j) { Final = max(Final, f[i] = j + 1); break; }
BL = 1, BR = RK[i + 1];
while (BL < BR) {
BMid = (BL + BR) >> 1;
if (Min(BMid, RK[i + 1]) >= j) BR = BMid;
else BL = BMid + 1;
}
A = (ST[0][BL] >= j) ? (BL - 1) : (BL), BL = RK[i + 1] + 1, BR = n;
while (BL < BR) {
BMid = (BL + BR + 1) >> 1;
if (Min(RK[i + 1] + 1, BMid) >= j) BL = BMid;
else BR = BMid - 1;
}
B = (ST[0][BL] >= j) ? (BL) : (BL - 1);
Ans = 0, N->Qry(1, n);
if (Ans >= j) { Final = max(Final, f[i] = j + 1); break; }
A = RK[i + j], B = f[i + j], --j, N->Add(1, n);
}
if (!f[i]) f[i] = 1;
}
printf("%u\n", Final);
return Wild_Donkey;
}
Day12: SAM & GSAM
后缀树
一棵压缩的 Trie, Trie 中存了所有后缀, 并且将 Trie 中的链压缩成一个点.
构造 Trie 的同时, 连接 gox,c, 指向点 x 的后缀前面加一个字符 c 得到的字符串所在的节点. 这样就能得到一个后缀自动机.
SAM
过水已隐藏
求第 k 大子串
在后缀自动机上记录 Size 然后在转移边上拓扑排序跑 DP.
求所有后缀的 LCP 总和
每个节点存自己子树中前缀结点个数 Size, 然后对每个点 i, 枚举它所有儿子, 对于儿子 j 统计 (Sizei−Sizej)∗Sizej∗Leni 即可, 复杂度 O(Sonx).
求长度 k 的子串出现次数最大值
建立 SAM, BFS 到深度为 k, 然后统计到达次数即可.
CF700E
一个字符串对另一个字符串是好的, 当且仅当这个字符串在另一个字符串中出现了两次.
求对于一个 S1, 最长有多少字符串满足 Si+1 对 Si 是好的.
建立 S1 的 SAM. 因为最优解中, 一定是 S1 的极大公共非自身前后缀 (也就是 Border) 是 S2, S2 的 Border 是 S3.
而很显然, 从 S1 到 Sk 所在的节点一定在后缀树上的一条链上.
然后就可以对 Si 在后缀树上倍增找 Si+1 了. 每个点 i 记录一个 fi, 表示它做 S1 的最大 k 值.
对于每个点 i, 用线段树合并处理出它的 EndPos 集合, 以及它集合中最右边的元素 Right, 然后倍增查询最深的满足 EndPos 在 [Righti−Leni+LenFaj−1,Righti) 存在元素的祖先 j, 则 fi=fj+1.
unsigned m, n, Cnt(0), Final, A, B, C, D, t, Ans(0), Tmp(0);
char aP[200005], * a(aP);
struct Seg {
Seg* LS, * RS;
char Val;
}S[10000005], * CntS(S);
void Insert(Seg* x, unsigned L, unsigned R) {
x->Val = 1;
if (L == R) { x->Val = 1; return; }
unsigned Mid((L + R) >> 1);
if (A <= Mid) Insert(x->LS = ++CntS, L, Mid);
else Insert(x->RS = ++CntS, Mid + 1, R);
}
void Qry(Seg* x, unsigned L, unsigned R) {
if ((A <= L) && (R <= B)) { Ans |= x->Val; return; }
unsigned Mid((L + R) >> 1);
if (A <= Mid) if (x->LS) Qry(x->LS, L, Mid);
if (B > Mid) if (x->RS) Qry(x->RS, Mid + 1, R);
}
Seg* Merge(Seg* x, Seg* y, unsigned L, unsigned R) {
unsigned Mid((L + R) >> 1);
if (y->LS) {
if (x->LS) { if (x->LS < x) *(++CntS) = *(x->LS), x->LS = CntS; x->LS = Merge(x->LS, y->LS, L, Mid); }
else x->LS = ++CntS, * CntS = *(y->LS);
}
if (y->RS) {
if (x->RS) { if (x->RS < x) *(++CntS) = *(x->RS), x->RS = CntS; x->RS = Merge(x->RS, y->RS, Mid + 1, R); }
else x->RS = ++CntS, * CntS = *(y->RS);
}
if (x->LS) x->Val |= x->LS->Val;
if (x->RS) x->Val |= x->RS->Val;
return x;
}
struct Node {
Node* Fa[18], * Bro, * Son, * To[26];
Seg* Root;
unsigned Len, Right, f;
}N[400005], * CntN(N), * Last(N);
void Add(const char x) {
Last->To[x] = ++CntN, CntN->Len = Last->Len + 1;
Node* Back(Last->Fa[0]);
Last = CntN;
while (Back) {
if (Back->To[x]) { break; }
Back->To[x] = Last;
Back = Back->Fa[0];
}
if (!Back) Last->Fa[0] = N;
else {
if (Back->To[x]->Len == Back->Len + 1) Last->Fa[0] = Back->To[x];
else {
Node* Bfr(Back->To[x]);
(++CntN)->Fa[0] = Bfr->Fa[0], CntN->Len = Back->Len + 1, Bfr->Fa[0] = CntN, Last->Fa[0] = CntN;
memcpy(CntN->To, Bfr->To, sizeof(Bfr->To));
while (Back) {
if (Back->To[x] == Bfr) Back->To[x] = CntN;
else break;
Back = Back->Fa[0];
}
}
}
}
void DFS1(Node* x) {
Node* Now(x->Son);
if (!(x->Root)) x->Root = ++CntS;
while (Now) {
for (char i(0); Now->Fa[i]; ++i) Now->Fa[i + 1] = Now->Fa[i]->Fa[i];
DFS1(Now);
x->Root = Merge(x->Root, Now->Root, 1, n);
x->Right = max(x->Right, Now->Right);
Now = Now->Bro;
}
}
void DFS2(Node* x) {
Node* Now(x->Son), * Jump(x);
for (char i(17); i >= 0; --i) {
if (Jump->Fa[i] > N) {
Ans = 0, A = x->Right - x->Len + Jump->Fa[i]->Fa[0]->Len + 1, B = x->Right - 1, Qry(Jump->Fa[i]->Root, 1, n);
if (!Ans) Jump = Jump->Fa[i];
}
}
if (Jump->Fa[0]) Final = max(Final, x->f = Jump->Fa[0]->f + 1);
while (Now) {
DFS2(Now);
Now = Now->Bro;
}
}
signed main() {
n = RD();
fread(a + 1, 1, n + 3, stdin);
while (a[1] < 'a') ++a;
for (unsigned i(1); i <= n; ++i) Add(a[i] -= 'a'), A = i, Insert(Last->Root = ++CntS, 1, n), Last->Right = i;
for (Node* i(N + 1); i <= CntN; ++i) i->Bro = i->Fa[0]->Son, i->Fa[0]->Son = i;
DFS1(N), DFS2(N);
printf("%u\n", Final);
return Wild_Donkey;
}
倍增找子串所在的节点
保存每个后缀所在的节点, Posi 表示的子串是 [1,i].
找子串 [a,b] 倍增找 Posb 的祖先 i, 使得 b−a+1∈(LenFai,Leni].
TJOI2016
给一个字符串, 每次询问子串 [a,b] 的子串和 [c,d] 的 LCP 长度.
注意, 这里并不是求 [a,b] 的子串和 [c,d] 的子串的 LCP, 而是求 [a,b] 的子串和 [c,d] 本身的 LCP, 我一开始读错题了, 以至于无论如何都是 O(qnlogn).
建立后缀自动机, 记 Posi 为前缀 [1,i] 对应的节点的指针.
二分答案, 判断 LCP 是 x 时是否成立.
如果 LCP 大于等于 x, 则子串 [c,c+x−1] 一定是 [a,b] 的子串.
这样就把二分答案的判断转化为了查询一个字符串是否是另一个字符串的子串的问题.
我们可以倍增找到 [c,c+x−1] 所在的节点, 判断它 EndPos 集合中 (也就是一些说法中的 Right 集合), 区间 [a+x−1,b] 中是否有值. 如果有, 说明它在对应的地方出现并且被 [a,b] 完全包含.
对于 EndPos 的计算, 区间查询, 就用线段树合并来解决. 但是这里的线段树合并和前面链接中提到的线段树合并的不同之处在于: 这里线段树合并之后还是有用的, 需要保护原树信息不被破坏, 而模板中的线段树合并之后不会访问, 所以只需要保证合并后的新树是正确的.
线段树合并, 对于后缀树上 EndPos 合并的问题, 线段树合并的时空复杂度是 O(logn) 的, 接下来是证明:
首先一开始会在每个前缀所在的节点的线段树中插入一个值, 一共是 n 个节点, 插入需要 O(logn) 的时空.
接下来是合并:
对于本问题, 只有合并的两棵线段树的交, 才会新建一个点, 而两棵线段树的并就是合并后的线段树. 定义一个点的 Size 是它子树中叶子的数量.
通过链接中对 EndPos 集合的几个性质的介绍, 我们知道合并的两棵线段树的叶子的交为 0.
两树的交中, 找出位置相同的两个点, x, y, 假设我们把 y 的信息合并到 x 上, 这时需要对 x 新建一个点 x′ 存储两点合并后的信息, 然后将 x′ 接到 x 的父亲上.
那么 Sizex′ 就是 Sizex+Sizey, 因为 Sizey>0, 所以 Sizex′ 一定大于 Sizex. 对于 x 所在的这个位置, 一共需要的点的数量最多就是这个位置在合并满的线段树上的 Size.
对于线段树上的每一层, Size 之和都是 n. 所以每一层需要的点数之和就是 n, 线段树一共有 O(logn) 层, 所以一共需要 O(nlogn) 个点. 因为每次执行 Merge 操作都是在新建节点之后, 所以时间复杂度等于空间复杂度.
最后是查询, 因为每次二分答案判断时需要 O(logn) 地倍增找对应节点, 也需要 O(logn) 对线段树进行区间查询, 所以一次询问的复杂度是 O(log2n).
加上一开始的构造自动机的 O(n) 和初始化倍增数组的 O(nlogn), 本题总复杂度 O(nlogn+qlog2n).
unsigned m, n, Cnt(0), A, B, C, D, Ans(0), QrL, QrR;
char aP[100005], * a(aP), Tmp(0);
struct Seg {
Seg* LS, * RS;
}S[5000005], * CntS(S);
void Insert(Seg* x, unsigned L, unsigned R) {
if (L == R) return;
unsigned Mid((L + R) >> 1);
if (A <= Mid) Insert(x->LS = ++CntS, L, Mid);
else Insert(x->RS = ++CntS, Mid + 1, R);
}
void Qry(Seg* x, unsigned L, unsigned R) {
if ((QrL <= L) && (R <= QrR)) { Tmp |= 1; return; }
unsigned Mid((L + R) >> 1);
if ((QrL <= Mid) && (x->LS)) Qry(x->LS, L, Mid);
if (Tmp) return;
if ((Mid < QrR) && (x->RS)) Qry(x->RS, Mid + 1, R);
}
void Merge(Seg* x, Seg* y, unsigned L, unsigned R) {
unsigned Mid((L + R) >> 1);
if (y->LS) {
if (x->LS) *(++CntS) = *(x->LS), x->LS = CntS, Merge(CntS, y->LS, L, Mid);
else x->LS = y->LS;
}
if (y->RS) {
if (x->RS) *(++CntS) = *(x->RS), x->RS = CntS, Merge(CntS, y->RS, Mid + 1, R);
else x->RS = y->RS;
}
}
struct Node {
Node* To[26], * Son, * Bro, * Fa[16];
Seg* Root;
unsigned Len;
}N[200005], * CntN(N), * Last(N), * Pos[100005];
void Add(const char x) {
(++CntN)->Len = Last->Len + 1;
Node* Back(Last);
Last = CntN;
while (Back) {
if (!(Back->To[x])) Back->To[x] = Last;
else break;
Back = Back->Fa[0];
}
if (!Back) Last->Fa[0] = N;
else {
if (Back->Len + 1 == Back->To[x]->Len) Last->Fa[0] = Back->To[x];
else {
Node* Bfr(Back->To[x]);
/*注意这里, Root 也会被复制, 要记得清除, 调了一上午的教训*/
*(++CntN) = *Bfr, Bfr->Fa[0] = CntN, Last->Fa[0] = CntN, CntN->Len = Back->Len + 1, CntN->Root = NULL;
while (Back) {
if (Back->To[x] == Bfr) Back->To[x] = CntN;
else break;
Back = Back->Fa[0];
}
}
}
}
void DFS(Node* x) {
Node* Now(x->Son);
if (!(x->Root)) x->Root = ++CntS;
while (Now) {
for (int i = 0; Now->Fa[i]; ++i) Now->Fa[i + 1] = Now->Fa[i]->Fa[i];
DFS(Now);
Merge(x->Root, Now->Root, 1, n);
Now = Now->Bro;
}
}
signed main() {
n = RD(), m = RD(), scanf("%s", a + 1), Pos[0] = N;
while (a[1] < 'a') ++a;
for (unsigned i(1); i <= n; ++i) Add(a[i] -= 'a'), Pos[i] = Last, A = i, Insert(Last->Root = ++CntS, 1, n);
for (Node* i(N + 1); i <= CntN; ++i) i->Bro = i->Fa[0]->Son, i->Fa[0]->Son = i;
DFS(N);
for (unsigned i(1); i <= m;++i) {
A = RD(), B = RD(), C = RD(), D = RD();
unsigned BL(1), BR(min(D - C + 1, B - A + 1)), BMid;
while (BL ^ BR) {
BMid = (BL + BR + 1) >> 1;
Node* Jump(Pos[C + BMid - 1]);
for (char i(15); i >= 0; --i) if ((Jump->Fa[i]) && (Jump->Fa[i]->Len >= BMid)) Jump = Jump->Fa[i];
Tmp = 0, QrL = A + BMid - 1, QrR = B, Qry(Jump->Root, 1, n);
if (Tmp) BL = BMid;
else BR = BMid - 1;
}
printf("%u\n", BL);
}
// system("pause");
return Wild_Donkey;
}
TJOI2015
给一个字符串, 询问字典序第 k 小的本质不同的子串, 询问字典序第 k 小的子串.
建立 SAM, DP 求出每个点求 Size 表示这个点转移边能转移到多少子串, 然后 DFS.
在转移边连接的 DAG 上, DP 出 Size. 表示从原点出发, 经过点 i 的所有路径所代表的字符串在查询中算多少种子串, DP 方程:
关于 Vali, 它的意义是从源点到 i 点的路径, 以 i 点结束, 在查询种算作几种子串. 很显然空串不能算入答案, 所以原点的 Val 为 0, 而其它点就要分类讨论了.
对于第一种询问, 本质相同的两个子串算作一个, 所以显然 Vali=1, 对于第二种询问, Vali 就是从原点到 i 的任意一条路径代表的字符串, 在原串中出现的次数, 所以这个值就是 i 在后缀树上的子树中, 前缀节点 (也就是 SAM 主链上的节点) 的数量. 在后缀树上 DFS 即可.
unsigned m, n, Cnt(0), Hd(0), Tl(0), A, B, C, D, t, Ans(0), Tmp(0);
char AddC, Opt;
struct Node {
Node* To[26], * Fail, * Son, * Bro;
unsigned long long Size;
unsigned Len, EndPos, Idg;
}N[1000005], * Topo[1000005], * CntN(N), * Last(N);
void Add() {
Node* Back(Last);
Last = ++CntN, Last->Len = Back->Len + 1, Last->EndPos = 1;
while (Back && (!(Back->To[AddC]))) { Back->To[AddC] = Last, Back = Back->Fail; }
if (Back) {
if (Back->To[AddC]->Len ^ (Back->Len + 1)) {
Node* Bfr(Back->To[AddC]);
*(++CntN) = *Bfr, CntN->Len = Back->Len + 1, Bfr->Fail = Last->Fail = CntN, CntN->EndPos = 0;
while (Back && (Back->To[AddC] == Bfr)) Back->To[AddC] = CntN, Back = Back->Fail;
}
else Last->Fail = Back->To[AddC];
}
else Last->Fail = N;
}
void DFS(Node* x) {
Node* Now(x->Son);
while (Now) DFS(Now), x->EndPos += Now->EndPos, Now = Now->Bro;
}
void Qry(Node* x) {
if (x->EndPos >= A) { putchar('\n'); return; } A -= x->EndPos;
for (char i(0); i < 26; ++i) if (x->To[i]) { if (x->To[i]->Size >= A) { putchar(i + 'a'); return Qry(x->To[i]); } A -= x->To[i]->Size; }
}
signed main() {
AddC = getchar();
while (AddC < 'a') AddC = getchar();
while (AddC >= 'a') AddC -= 'a', Add(), AddC = getchar();
for (Node* i(N); i <= CntN; ++i) for (char j(0); j < 26; ++j) if (i->To[j]) ++(i->To[j]->Idg);
Topo[++Tl] = N, n = CntN - N;
while (Hd ^ Tl) for (char i(!(++Hd)); i < 26; ++i) if (Topo[Hd]->To[i]) if (!(--(Topo[Hd]->To[i]->Idg))) Topo[++Tl] = Topo[Hd]->To[i];
Opt = RD(), A = RD();
if (Opt) {
for (Node* i(N + 1); i <= CntN; ++i) i->Bro = i->Fail->Son, i->Fail->Son = i;
DFS(N), N->EndPos = 0;
}
else for (Node* i(N + 1); i <= CntN; ++i) i->EndPos = 1;
for (unsigned i(n + 1); i; --i) {
Topo[i]->Size = Topo[i]->EndPos;
for (char j(0); j < 26; ++j) if (Topo[i]->To[j]) Topo[i]->Size += Topo[i]->To[j]->Size;
}
if (N->Size < A) { printf("-1\n"); return 0; }
Qry(N);
return Wild_Donkey;
}
NOI2018
给一个字符串, 每次给一个模式串 T 求有多少本质不同的子串不是 S 的子串 [l,r] 的子串.
对 S 构造后缀自动机, 记录后缀树的 DFS 序和子树大小, 用以 DFSr 为序的线段树维护区间最大值, 用来查询每个点的 EndPos 集合的最大值.
离线所有询问, 按 r 排序, 然后对于每个询问 i, 保证 ≤ri 的 Endpos 都被插入了, 这样就能查询一个点代表的子串在 ri 之前最后一次出现的位置.
对于询问的字符串 Ti, 从左到右从 S 的 SAM 上识别, 维护当前考虑过的 Ti 的前缀, 和 S 的 [li,ri] 中的子串的 LCS (Longest Common Suffix).
同时构造 Ti 的 SAM, 在 SAM 中插入刚刚考虑的字符, 得到这个前缀的节点 Now, 求出 max(0,LCS−Now−>Fail−>Len), 统计得到 Ti 和 S 的 [li,ri] 子串的本质不同的公共子串数量.
最后在 Ti 的 SAM 中统计本质不同的子串数, 减去本质不同公共子串数, 得到所求答案.
unsigned long long Ans[100005];
unsigned m, n, Cnt(0), B, C, D, t, Calc;
unsigned LCS, Pointer(0), DFSCnt(0), Tmp(0);
char b[1000005], CTmp;
struct Ask {
unsigned Frm, To, L, R, AsNum;
inline const char operator <(const Ask& x) { return this->R < x.R; }
}A[100005];
struct Seg {
Seg* LS, * RS;
unsigned Mx;
}S[2000005], * CntS(S);
void Insert(Seg* x, unsigned L, unsigned R) {
x->Mx = max(x->Mx, C);
if (L == R) return;
unsigned Mid((L + R) >> 1);
if (B <= Mid) { if (!(x->LS)) x->LS = ++CntS; Insert(x->LS, L, Mid); }
else { if (!(x->RS)) x->RS = ++CntS; Insert(x->RS, Mid + 1, R); }
}
void Qry(Seg* x, unsigned L, unsigned R) {
if ((B <= L) && (R <= C)) { D = max(D, x->Mx);return; }
unsigned Mid((L + R) >> 1);
if ((B <= Mid) && (x->LS)) Qry(x->LS, L, Mid);
if ((Mid < C) && (x->RS)) Qry(x->RS, Mid + 1, R);
}
struct Node {
Node* To[26], * Fail, * Son, * Bro;
unsigned Len, DFSr, Size;
}N[2000005], * Prefix[500005], * CntN(N), * Last(N), * DelLine(N), * Search, * Choice;
void Add() {
Node* Back(Last);
Last = ++CntN, CntN->Len = Back->Len + 1, memset(Last->To, 0, sizeof(Last->To));
while (Back && (!(Back->To[CTmp]))) Back->To[CTmp] = Last, Back = Back->Fail;
if (Back) {
if ((Back->To[CTmp]->Len) ^ (Back->Len + 1)) {
Node* Bfr(Back->To[CTmp]);
*(++CntN) = *Bfr, CntN->Len = Back->Len + 1, Bfr->Fail = Last->Fail = CntN;
while (Back && (Back->To[CTmp] == Bfr)) Back->To[CTmp] = CntN, Back = Back->Fail;
}
else Last->Fail = Back->To[CTmp];
}
else Last->Fail = DelLine;
}
void DFS(Node* x) {
Node* Now(x->Son);
x->DFSr = ++DFSCnt, x->Size = 1;
while (Now) {
DFS(Now), x->Size += Now->Size, Now = Now->Bro;
}
}
signed main() {
CTmp = getchar(); while (CTmp < 'a') CTmp = getchar();
while (CTmp >= 'a') CTmp -= 'a', Add(), Prefix[++n] = Last, CTmp = getchar();
DelLine = Prefix[n] + 2, m = RD();
for (unsigned i(1); i <= m; ++i) {
A[i].Frm = Pointer + 1, CTmp = getchar(); while (CTmp < 'a') CTmp = getchar();
while (CTmp >= 'a') b[++Pointer] = CTmp - 'a', CTmp = getchar();
A[i].L = RD(), A[i].R = RD(), A[i].To = Pointer, A[i].AsNum = i;
}
for (Node* i(N + 1); i <= CntN; ++i) i->Bro = i->Fail->Son, i->Fail->Son = i;
A[m + 1].R = A[m].R, sort(A + 1, A + m + 1), DFS(N);
for (unsigned i(1); i <= A[1].R; ++i) B = Prefix[i]->DFSr, C = i, Insert(S, 1, Prefix[n] - N + 2);
for (unsigned i(1); i <= m; ++i) {
LCS = 0, Search = N, Last = CntN = DelLine, memset(DelLine, 0, sizeof(Node)), Tmp = 0;
for (unsigned j(A[i].Frm); j <= A[i].To; ++j) {
Calc = 0, Choice = NULL;
while (Search && (Search->Len >= Calc)) {
if (Search->To[b[j]]) {
B = Search->To[b[j]]->DFSr, C = B + Search->To[b[j]]->Size - 1, D = 0, Qry(S, 1, Prefix[n] - N + 2);
if (D >= A[i].L) {
if (D >= A[i].L + Search->Len) {
if (Calc < Search->Len + 1) Calc = Search->Len + 1, Choice = Search->To[b[j]]; break;
}
if (Calc < min(Search->Len + 1, D - A[i].L + 1))
Calc = min(Search->Len + 1, D - A[i].L + 1), Choice = Search->To[b[j]];
}
}
Search = Search->Fail;
}
Search = (Choice) ? Choice : (N + 1);
LCS = min((unsigned)LCS + 1, Calc), CTmp = b[j], Add(), Tmp += (Last->Fail->Len <= LCS) ? (LCS - Last->Fail->Len) : 0;
}
for (Node* j(DelLine + 1); j <= CntN; ++j) Ans[A[i].AsNum] += j->Len - j->Fail->Len;
Ans[A[i].AsNum] -= Tmp;
for (unsigned j(A[i].R + 1); j <= A[i + 1].R; ++j) B = Prefix[j]->DFSr, C = j, Insert(S, 1, Prefix[n] - N + 2);
}
for (unsigned i(1); i <= m; ++i) printf("%llu\n", Ans[i]);
return Wild_Donkey;
}
GSAM
过水已隐藏
ZJOI2015
给⼀个叶⼦数不超过 20 的 Trie, 但是与一般 Trie 不同的是, 它可以将任意一条路径作为一个字符串, 而不是只有从上往下的路径, 求有多少个不同的字符串.
分别以每个叶子作为根, 并成一棵新的 Trie. BFS 新的 Trie, 建 GSAM. 然后统计本质不同子串数量.
unsigned m, n, Cnt(0), A, B, t, Tmp(0);
unsigned Tl(0), Hd(0), Cls;
unsigned long long Ans;
struct Tr;
struct Edge {
Tr* To;
Edge* Nxt;
}E[200005], * CntE(E);
struct Tr {
Edge* Fst;
unsigned Deg;
char Cr;
}IT[100005];
struct Node {
Node* To[10], * Fail;
unsigned Len;
}N[4000005], * CntN(N), * Last(N);
struct Trie {
Trie* To[10];
Node* Am;
}T[2000005], * Q[2000005], * CntT(T);
void Link(Tr* x, Tr* y) { (++CntE)->Nxt = x->Fst, x->Fst = CntE, CntE->To = y, ++(x->Deg); }
void DFS(Tr* x, Tr* y, Trie* z) {
Edge* Sid(x->Fst);
if (!(z->To[x->Cr])) z->To[x->Cr] = ++CntT; z = z->To[x->Cr];
while (Sid) {
if (Sid->To != y) {
DFS(Sid->To, x, z);
}
Sid = Sid->Nxt;
}
}
Node* Add(char x) {
Node* Back(Last), * Cur(++CntN);
Cur->Len = Last->Len + 1;
while (Back) {
if (!(Back->To[x])) Back->To[x] = Cur;
else break;
Back = Back->Fail;
}
if (Back) {
if (Back->To[x]->Len == Back->Len + 1) {
Cur->Fail = Back->To[x];
}
else {
Node* Bfr(Back->To[x]);
*(++CntN) = *(Back->To[x]);
CntN->Len = Back->Len + 1, Bfr->Fail = Cur->Fail = CntN;
while (Back && (Back->To[x] == Bfr)) Back->To[x] = CntN, Back = Back->Fail;
}
}
else {
Cur->Fail = N;
}
return Cur;
}
signed main() {
n = RD(), Cls = RD();
for (unsigned i(1); i <= n; ++i) IT[i].Cr = RD();
for (unsigned i(1); i < n; ++i)
A = RD(), B = RD(), Link(IT + A, IT + B), Link(IT + B, IT + A);
for (unsigned i(1); i <= n; ++i) if (IT[i].Deg == 1) DFS(IT + i, NULL, T);
Q[++Tl] = T, T->Am = N;
while (Tl ^ Hd) {
Trie* Now(Q[++Hd]);
Last = Now->Am;
for (unsigned i(0); i < Cls; ++i) if (Now->To[i]) Now->To[i]->Am = Add(i), Q[++Tl] = Now->To[i];
}
for (Node* i(N + 1); i <= CntN; ++i) Ans += i->Len - i->Fail->Len;
printf("%llu\n", Ans);
return Wild_Donkey;
}
BZOJ4545
给一棵 Trie, 支持三种操作:
-
求本质不同的子串数量
-
插入一个子树
-
询问一个字符串出现了多少次
这是第一次写在线 GSAM, 确实遇到不少细节.
求本质不同子串数量可以在插入过程中, 直接维护一个全局变量.
而第三种操作, 需要询问一个点后缀树上子树信息和, 普遍的做法是用 LCT 在线维护.
但是有一种离线做法, 仅用树状数组就可以回答询问, 首先我们知道在插入过程中, 一个点后缀树上的点只会增加不会减少, 所以在构造完之后, DFS 后缀树, 然后对每个点记录 Size, 那么它的子树的 DFS 序形成一个区间 [DFSrx,DFSrx+Sizex−1], 记录构造过程中, 对点的权值修改的操作序列, 用树状数组维护单点增加, 区间求和即可.
unsigned long long Ans[100005], Sum;
unsigned Map[100005], Qry[100005][3], Edit[1000005], CntE(0);
unsigned m, n, DFSCnt(0), Cnt(0);
unsigned A, B, D, t, Tmp(0);
unsigned TrArray[200005], ULimit;
char C;
void Chg(unsigned x) { while (x <= ULimit) ++TrArray[x], x += Lowbit(x); }
void Que(unsigned x) { while (x) Tmp += TrArray[x], x -= Lowbit(x); }
struct Node {
Node* To[26], * Fail, * Bro, * Son;
unsigned Len, DFSr, Size;
}N[200005], * CntN(N), * Search, * Last;
void Add() {
if (Last->To[C]) {
if (Last->To[C]->Len == Last->Len + 1) { Map[B] = Last->To[C] - N;return; }
Node* Bfr(Last->To[C]), * x(++CntN);
x->Fail = Bfr->Fail, Bfr->Fail = x, x->Len = Last->Len + 1, Map[B] = x - N;
for (char i(0); i < 26; ++i) if ((Bfr->To[i]) && (Bfr->To[i]->Len)) x->To[i] = Bfr->To[i];
while (Last && (Last->To[C] == Bfr)) Last->To[C] = x, Last = Last->Fail;
return;
}
Node* x(++CntN);
x->Len = Last->Len + 1, Map[B] = x - N;
while (Last) {
if (Last->To[C]) break; else Last->To[C] = x;
Last = Last->Fail;
}
if (Last) {
if (Last->To[C]->Len == Last->Len + 1) { x->Fail = Last->To[C], Sum += x->Len - Last->To[C]->Len; return; }
Node* Bfr(Last->To[C]);
(++CntN)->Len = Last->Len + 1, CntN->Fail = Bfr->Fail, Bfr->Fail = x->Fail = CntN, Sum += x->Len - CntN->Len;
for (char i(0); i < 26; ++i) if ((Bfr->To[i]) && (Bfr->To[i]->Len)) CntN->To[i] = Bfr->To[i];
while (Last && (Last->To[C] == Bfr)) Last->To[C] = CntN, Last = Last->Fail;
}
else x->Fail = N + 1, Sum += x->Len;
}
void DFS_Final(Node* x) {
x->DFSr = ++DFSCnt, x->Size = 1;
Node* Now(x->Son);
while (Now) DFS_Final(Now), x->Size += Now->Size, Now = Now->Bro;
}
signed main() {
RD(), n = RD(), memset(Ans, 0x3f, sizeof(Ans)), Map[1] = ++CntN - N;
for (register unsigned i(1); i < n; ++i) {
A = RD(), B = RD(), C = getchar(); while (C < 'a') C = getchar();
if (A > B) swap(A, B);
C -= 'a', Last = N + Map[A], Add(), Edit[++CntE] = Map[B];
}
m = RD();
for (unsigned i(1); i <= m; ++i) {
D = RD();
if (D == 1) Ans[i] = Sum;
else {
if (D & 1) {
C = getchar(), Search = N + 1;
while (C < 'a') C = getchar();
while (C >= 'a') {
if (!(Search->To[C - 'a'])) { Ans[i] = 0; while (C >= 'a') C = getchar(); break; }
Search = Search->To[C - 'a'], C = getchar();
}
if (Ans[i]) Qry[++Cnt][1] = Search - N, Qry[Cnt][0] = i, Qry[Cnt][2] = CntE;
}
else {
RD(), D = RD();
for (unsigned j(1); j < D; ++j) {
A = RD(), B = RD(), C = getchar(); while (C < 'a') C = getchar();
if (A > B) swap(A, B);
C -= 'a', Last = N + Map[A], Add(), Edit[++CntE] = Map[B];
}
}
}
}
for (Node* i(N + 2); i <= CntN; ++i) i->Bro = i->Fail->Son, i->Fail->Son = i;
DFS_Final(N + 1), ULimit = CntN - N;
for (unsigned i(1), j(1); i <= Cnt; ++i) {
while (j <= Qry[i][2]) { Chg(N[Edit[j]].DFSr), ++j; }
Tmp = 0, Que(N[Qry[i][1]].DFSr + N[Qry[i][1]].Size - 1), Ans[Qry[i][0]] = Tmp, Tmp = 0, Que(N[Qry[i][1]].DFSr - 1), Ans[Qry[i][0]] -= Tmp;
}
for (unsigned i(1); i <= m; ++i) if (Ans[i] < 0x3f3f3f3f3f3f3f3f) printf("%llu\n", Ans[i]);
return Wild_Donkey;
}
求多少子串是 n 个字符串中至少 k 个字符串的子串
建立 GSAM, 每个点存一个 Cnt 记录多少个字符串存在这个点, 然后对后缀自动机进行 DP, 只走那些 Cnt≥k 的节点.
Day13: 模拟赛
A
给一个字符串, 判断它是否是一个字符串连续写两次后插入一个字符得到的, 如果可以构造并且唯一, 输出这个字符串.
分类讨论插入在第一次写还是第二次写的地方, 然后线性匹配, 如果失配, 有一次跳过的机会, 说明跳过的位置是插入的位置.
如果跳过后仍失配, 则这种情况不合法.
对于两种情况, 如果只有一种匹配成功, 则直接输出对应字符串.
如果都不成功, 则无解.
如果两个都匹配成功, 对两个答案跑匹配, 如果仍匹配, 直接输出答案, 否则答案不唯一.
unsigned m, n, Cnt(0), Flg(0), A, B, C, D, t, Ans1(0), Ans2(0), Tmp(0);
char a[2000005];
int main() {
n = RD(), m = n >> 1;
if(!(n & 1)) {
printf("NOT POSSIBLE\n");
return 0;
}
fread(a + 1, 1, 2000002, stdin);
Flg = 0;
for (register unsigned i(1); i <= m; ++i) {
if(a[i] ^ a[i + Flg + m]) {
if(Flg) {
Ans1 = 0x3fffffff;
break;
}
if(a[i] == a[i + m + 1]) {
Ans1 = 1;
Flg = 1;
} else {
Ans1 = 0x3fffffff;
break;
}
}
}
Flg = 0;
for (register unsigned i(1); i <= m; ++i) {
if(a[i + Flg] ^ a[i + m + 1]) {
if(Flg) {
Ans2 = 0x3fffffff;
break;
}
if(a[i + 1] == a[i + m + 1]) {
Ans2 = 1;
Flg = 1;
} else {
Ans2 = 0x3fffffff;
break;
}
}
}
if((Ans1 > 0x3f3f3f3f) && (Ans2 > 0x3f3f3f3f)) {
printf("NOT POSSIBLE\n");
return 0;
}
if((Ans1 < 0x3f3f3f3f) && (Ans2 < 0x3f3f3f3f)) {
for (register unsigned i(1); i <= m; ++i) {
if(a[i] != a[i + m + 1]) {
printf("NOT UNIQUE\n");
return 0;
}
}
}
if(Ans1 < 0x3f3f3f3f) {
for (register unsigned i(1); i <= m; ++i) {
putchar(a[i]);
}
putchar('\n');
return 0;
}
for (register unsigned i(m + 2); i <= n; ++i) {
putchar(a[i]);
}
putchar('\n');
return Wild_Donkey;
}
B
给一个环, 每次选择 ai, 给左右两个相邻的数加上 ai, 将 ai 变成 −ai. 求最少操作次数, 使得所有数非负.
发现总和永远不变, 所以 Sum<0 时不可能有解.
而 Sum=0 也不会有解, 因为无论如何都不能给出状态 0 0...0 0 0 是如何变换来的.
所以有解当且仅当 Sum≥1 的时候有解.
虽然赛时的数据结构优化贪心被卡成筛子 (暴力有 28′), 但是这篇代码仍然可圈可点, 因为它将人类的创造力和行为艺术发挥到了极致.
每次选择序列中最小的元素, 然后对它进行如此操作, 用线段树维护这个序列, O(1) 取最小值, O(logn) 修改.
操作过程中统计操作次数, 直到最小值非负跳出程序.
接下来是这篇伟大的得了 11′ 的代码, 复杂度 n∑ailogn.
unsigned a[200005], m, n, Cnt(0), A, B, C, D, t, Sum(0), Ans(0), Tmp(0);
struct Node {
Node *LS, *RS;
unsigned Val, Pos, Min;
}N[400005], *CntN(N);
inline void Clr() {
n = RD(), Sum = 0, CntN = N, Cnt = 0;
}
void Udt(Node *x) {
if(x->LS->Val <= x->RS->Val) {
x->Val = x->LS->Val;
x->Pos = x->LS->Pos;
} else {
x->Val = x->RS->Val;
x->Pos = x->RS->Pos;
}
}
void Build(Node *x, unsigned L, unsigned R) {
if(L == R) {
x->LS = x->RS = NULL;
x->Min = a[L], x->Pos = L, x->Val = 0x3f3f3f3f;
return;
}
register unsigned Mid = ((L + R) >> 1);
Build(x->LS = ++CntN, L, Mid);
Build(x->RS = ++CntN, Mid + 1, R);
x->Min = min(x->LS->Min, x->RS->Min);
Udt(x);
}
void Chg(Node *x, unsigned L, unsigned R) {
if(L == R) {
x->Val = B, x->Pos = A;
return;
}
register unsigned Mid((L + R) >> 1);
if(A <= Mid) Chg(x->LS, L, Mid);
else Chg(x->RS, Mid + 1, R);
Udt(x);
}
void Chg2(Node *x, unsigned L, unsigned R) {
if(L == R) {
x->Min = a[A];
return;
}
register unsigned Mid((L + R) >> 1);
if(A <= Mid) Chg2(x->LS, L, Mid);
else Chg2(x->RS, Mid + 1, R);
x->Min = min(x->LS->Min, x->RS->Min);
}
void Add (unsigned x) {
A = x;
if(a[x] < 1000000) {
B = 2000000 - a[x];
if(x == 1) {
if(a[n] > 1000000) B -= min(1000000 - a[x], a[n] - 1000000);
} else {
if(a[x - 1] > 1000000) B -= min(1000000 - a[x], a[x - 1] - 1000000);
}
if(x == n) {
if(a[1] > 1000000) B -= min(1000000 - a[x], a[1] - 1000000);
} else {
if(a[x + 1] > 1000000) B -= min(1000000 - a[x], a[x + 1] - 1000000);
}
Chg(N, 1, n);
} else {
B = 0x3f3f3f3f;
Chg(N, 1, n);
}
}
int main() {
while (1){
Clr();
if(!n) break;
for (register unsigned i(1); i <= n; ++i) {
Sum += (a[i] = (RDsg() + 1000000));
}
if(Sum <= (n * 1000000)) {
printf("-1\n");
continue;
}
Build(N, 1, n);
if(N[0].Min >= 1000000) {
printf("0\n");
continue;
}
for (register unsigned i(1); i <= n; ++i) {
Add(i);
}
register unsigned Now;
while (N[0].Min < 1000000) {
++Cnt;
Now = N[0].Pos;
if(Now == 1) {
a[n] -= 1000000 - a[Now];
A = n;
Chg2(N, 1, n);
} else {
a[Now - 1] -= 1000000 - a[Now];
A = Now - 1;
Chg2(N, 1, n);
}
if(Now == n) {
a[1] -= 1000000 - a[Now];
A = 1;
Chg2(N, 1, n);
} else {
a[Now + 1] -= 1000000 - a[Now];
A = Now + 1;
Chg2(N, 1, n);
}
a[Now] = 2000000 - a[Now];
A = Now;
Chg2(N, 1, n);
Add(Now);
if(Now == 1) Add(n);
else Add(Now - 1);
if(Now == n) Add(1);
else Add(Now + 1);
}
printf("%u\n", Cnt);
}
return Wild_Donkey;
}
然后在好心的 JJK 的提醒下, 我的贪心太小心了, 这个题可以直接见到负数就修改, 于是可以多源 BFS.
队列里存储所有负数, 发现每次操作除了操作的数字, 不存在别的位置的数变大的情况, 所以队列一定是只能在队首弹出的, 而每次可能变成负数的也只有操作数字两侧的数字, 所以可以每次只判断两个数是否入队.
这份代码得了 28′, 堪称用更短的代码拿更多的分的典范.
复杂度貌似是 O(n∑ai).
int a[200005];
long long Sum(0);
unsigned Q[100000005], Tl, Hd, m, n, Cnt(0);
unsigned A, B, C, D, t, Ans(0), Tmp(0);
char InQue[200005];
inline void Clr() {
n = RD(), Sum = 0, Tl = Hd = 0, Cnt = 0;
}
int main() {
while (1) {
Clr();
if (!n) break;
for (unsigned i(1); i <= n; ++i) Sum += (a[i] = RDsg());
if (Sum <= 0) { printf("-1\n");continue; }
for (register unsigned i(1); i <= n; ++i) if (a[i] < 0) Q[++Tl] = i, InQue[i] = 1;
while (Tl ^ Hd) {
unsigned Now(Q[++Hd]);
++Cnt, InQue[Now] = 0;
if (Now == 1) { a[n] += a[Now]; if ((!InQue[n]) && (a[n] < 0)) Q[++Tl] = n, InQue[n] = 1; }
else { a[Now - 1] += a[Now]; if ((!InQue[Now - 1]) && (a[Now - 1] < 0)) Q[++Tl] = Now - 1, InQue[Now - 1] = 1; }
if (Now == n) { a[1] += a[Now]; if ((!InQue[1]) && (a[1] < 0)) Q[++Tl] = 1, InQue[1] = 1; }
else { a[Now + 1] += a[Now]; if ((!InQue[Now + 1]) && (a[Now + 1] < 0)) Q[++Tl] = Now + 1, InQue[Now + 1] = 1; }
a[Now] = -a[Now];
}
printf("%u\n", Cnt);
}
return Wild_Donkey;
}
因为要求所有元素非负, 所以最终序列前缀和 (包括第 0 位) 一定是单调不降并且极差等于 m.
发现每次对 i 执行操作是交换 i 和 i−1 的前缀和. 但是当 i=n 或 i=1 的时候并不是这样.
但是当断点右移的时候, 如果只看相对大小, 那么前缀和数组相当于取出第一个元素, 增加 Sum 放到末尾后面, 这样就可以写出同时加上第一个元素的前缀和, 也可以取最后一个元素, 减去 Sum 放到末尾.
于是又有一个贪心, 每次将前 [1,n) 的序列排序 (我们可以直接交换这些元素, 从而实现排序), 然后统计入答案, 取第一个元素加 Sum 放到末尾, 将第一个元素弹出.
显然可以通过平衡树维护逆序对从而将时间复杂度优化到 O(∑ailogn).
int a[200005];
long long Sum[200005], A, B, m;
unsigned n;
unsigned C, D, t, Ans(0), Tmp(0);
char InQue[200005];
struct Node {
Node* LS, * RS;
long long ValL, ValR;
unsigned Size;
}N[400005], * Stack[400005], ** Top(Stack), * Root(N);
inline void Clr() {
n = RD(), Tmp = Ans = 0, Root = N, Top = Stack;
}
Node* Insert(Node* x) {
++x->Size;
if (x->Size == 2) {
Node* Now(*(Top--));
Now->ValL = Now->ValR = A, Now->Size = 1, Now->LS = Now->RS = NULL;
if (A > x->ValL) x->RS = Now, x->LS = *(Top--), x->LS->Size = 1, x->LS->LS = x->LS->RS = NULL, x->LS->ValL = x->LS->ValR = x->ValL;
else x->LS = Now, x->RS = *(Top--), x->RS->Size = 1, x->RS->LS = x->RS->RS = NULL, x->RS->ValL = x->RS->ValR = x->ValR;
x->ValL = x->LS->ValL, x->ValR = x->RS->ValR;
return x;
}
if ((x->LS) && (x->LS->ValR >= A)) x->LS = Insert(x->LS), x->ValL = x->LS->ValL;
else x->RS = Insert(x->RS), x->ValR = x->RS->ValR;
if (!(x->LS)) { *(++Top) = x; return x->RS; }
if (!(x->RS)) { *(++Top) = x; return x->LS; }
if (x->Size > 3) {
if ((x->LS->Size << 1) < x->RS->Size) {
Node* Now(x->RS);
x->RS = Now->RS, Now->RS = Now->LS, Now->LS = x->LS, x->LS = Now;
Now->ValL = Now->LS->ValL, Now->ValR = Now->RS->ValR;
Now->Size = Now->LS->Size + Now->RS->Size;
}
if ((x->RS->Size << 1) < x->LS->Size) {
Node* Now(x->LS);
x->LS = Now->LS, Now->LS = Now->RS, Now->RS = x->RS, x->RS = Now;
Now->ValL = Now->LS->ValL, Now->ValR = Now->RS->ValR;
Now->Size = Now->LS->Size + Now->RS->Size;
}
}
return x;
}
Node* Del(Node* x) {
--(x->Size);
if (!(x->Size)) { *(++Top) = x; return NULL; }
if ((x->LS) && (x->LS->ValR >= A)) { x->LS = Del(x->LS); }
else { x->RS = Del(x->RS); }
if (!(x->LS)) { *(++Top) = x; return x->RS; }
if (!(x->RS)) { *(++Top) = x; return x->LS; }
if (x->Size > 3) {
if ((x->LS->Size << 1) < x->RS->Size) {
Node* Now(x->RS);
x->RS = Now->RS, Now->RS = Now->LS, Now->LS = x->LS, x->LS = Now;
Now->ValL = Now->LS->ValL, Now->ValR = Now->RS->ValR;
Now->Size = Now->LS->Size + Now->RS->Size;
}
if ((x->RS->Size << 1) < x->LS->Size) {
Node* Now(x->LS);
x->LS = Now->LS, Now->LS = Now->RS, Now->RS = x->RS, x->RS = Now;
Now->ValL = Now->LS->ValL, Now->ValR = Now->RS->ValR;
Now->Size = Now->LS->Size + Now->RS->Size;
}
}
x->ValL = x->LS->ValL, x->ValR = x->RS->ValR;
return x;
}
unsigned Find(Node* x) {
if (x->Size == 1) return (unsigned)(x->ValL > A);
if ((x->RS) && (x->RS->ValL > A)) return ((x->LS) ? (Find(x->LS) + x->RS->Size) : x->RS->Size);
else return Find(x->RS);
}
int main() {
while (1) {
Clr();
if (!n) break;
for (unsigned i(1); i <= n; ++i) Sum[i] = Sum[i - 1] + (a[i] = RDsg());
for (unsigned i(1); i <= (n << 1); ++i) *(++Top) = N + i;
m = Sum[n], N->ValL = N->ValR = a[1], N->Size = 1, N->LS = N->RS = 0;
if (m <= 0) { printf("-1\n");continue; }
for (register unsigned i(2); i < n; ++i) A = Sum[i], Ans += Find(Root), Root = Insert(Root);
A = m, Tmp = Find(Root), Root = Insert(Root), B = Root->ValL;
while (Root->ValL + m < Root->ValR) {
Ans += Tmp;
A = B, Root = Del(Root);
A += m, Tmp = Find(Root), B = Root->ValL, Root = Insert(Root);
}
printf("%u\n", Ans + Tmp);
}
return Wild_Donkey;
}
但是很遗憾, 这份代码没有得分, 因为它是假的, 每次不一定需要取最小的, 也没有必要维护 [1,n) 前缀和单增, 只需要取最靠左的 ≤Max−m 的数字放到末尾, 然后答案加上这个数字到左端的交换数即可. 如果没有这样的数字, 则取最小值. 直到极差等于 m 为止.
但是这样极难维护, 而且算法复杂度 O(∑ailogn) 和 O(n2logn) 同阶, 也不是对的.
单调不降还要求前缀和数组第 1 位大于等于第 0 位, 也就是前缀和数组不能出现负数.
所以我们可以在任意一个位置开始求前缀和, 取最小值出现的位置, 然后以该点为末尾, 该点之后的一个元素为起点, 求出新的前缀和数组, 则这个新的前缀和一定都大于等于 0.
证明也很简单, 因为 Sum≤0 的情况已经输出 −1 了, 所以 Sum>0.
又因为前缀和相当于是一个折线, 而这个折线终点到起点的高度差就是 Sum, 起点可以认为是 0. 因为问题是一个环, 所以这个折线可以在自己的终点处再连接无数个自己, 相当于在环上循环求前缀和, 每个循环跑一圈, 前缀和增加 Sum.
那么就可以尝试找出这个折线的最低点, 以这里为起点, 那么再它后面的一个循环中, 一定不会有点低于它, 又因为这个最低点的值是 0, 所以折线上不存在负数.
发现只要我们愿意, 一定能在逆序对的数量次交换中得到有序的序列, 而这个交换次数是不可避免的, 所以不如一开始就将数组排序, 然后将逆序对数统计到答案中.
找到这个断开的位置, 重新求出前缀和, 求出逆序对数量, 然后记录进入答案. 这时就可以排序了.
接下来考虑减少极差.
我们取第一个元素 a, 增加 Sum 放到末尾, 但是这样会产生 x 逆序对, 将 x 加入答案即可再次得到单调序列.
发现每次进行这个操作后, a 到每个比它大超过 Sum 的元素的差就会减少 m, 所以每对数字 a<b, 都会贡献 ⌊b−a−1)Sum⌋ 的答案.
所以我们需要做的就是将前缀和 S 数组排序, 然后统计两两差 ⌊(Difi,j−1)Sum⌋ 的总和.
因为 Sum 非常小, 所以我们可以考虑将 S 对 modSum 进行分类, 对每个 Si 枚举前面的数对 Sum 的模数, 统计答案.
本来是可以用离散化和树状数组干过去的, 但是我舍不得我的平衡树, 所以我就用平衡树求逆序对了.
long long a[100005], b[100005];
long long Sum[100005], Min, m(0), Pos;
long long A, Pls[15], Ans;
long long n, Cnt, PCnt[15], Last;
struct Node {
Node* LS, * RS;
long long ValL, ValR;
unsigned Size;
}N[200005], * CntN(N), * Root(N);
inline void Clr() {
// printf("Done?\n");
if (m > 0) memset(Pls, 0, m << 3), memset(PCnt, 0, m << 3);
// printf("Half\n");
n = RD(), Ans = 0, Min = 0x3f3f3f3f3f3f3f3f, Root = CntN = N;
// printf("Done!\n");
}
void Print(Node* x) {
printf("Size %u [%lld, %lld] LS %u, RS %u\n", x->Size, x->ValL, x->ValR, x->LS - N, x->RS - N);
}
Node* Insert(Node* x) {
++x->Size;
if (x->Size == 2) {
Node* Now(++CntN);
Now->ValL = Now->ValR = A, Now->Size = 1, Now->LS = Now->RS = NULL;
if (A > x->ValL) x->RS = Now, x->LS = ++CntN, x->LS->Size = 1, x->LS->LS = x->LS->RS = NULL, x->LS->ValL = x->LS->ValR = x->ValL;
else x->LS = Now, x->RS = ++CntN, x->RS->Size = 1, x->RS->LS = x->RS->RS = NULL, x->RS->ValL = x->RS->ValR = x->ValR;
x->ValL = x->LS->ValL, x->ValR = x->RS->ValR;
return x;
}
if ((x->LS) && (x->LS->ValR >= A)) x->LS = Insert(x->LS), x->ValL = x->LS->ValL;
else x->RS = Insert(x->RS), x->ValR = x->RS->ValR;
if (!(x->LS)) { return x->RS; }
if (!(x->RS)) { return x->LS; }
if (x->Size > 3) {
if ((x->LS->Size << 1) < x->RS->Size) {
Node* Now(x->RS);
x->RS = Now->RS, Now->RS = Now->LS, Now->LS = x->LS, x->LS = Now;
Now->ValL = Now->LS->ValL, Now->ValR = Now->RS->ValR;
Now->Size = Now->LS->Size + Now->RS->Size;
}
if ((x->RS->Size << 1) < x->LS->Size) {
Node* Now(x->LS);
x->LS = Now->LS, Now->LS = Now->RS, Now->RS = x->RS, x->RS = Now;
Now->ValL = Now->LS->ValL, Now->ValR = Now->RS->ValR;
Now->Size = Now->LS->Size + Now->RS->Size;
}
}
return x;
}
unsigned Find(Node* x) {
if (x->Size == 1) return (unsigned)(x->ValL > A);
if ((x->RS) && (x->RS->ValL > A)) return ((x->LS) ? (Find(x->LS) + x->RS->Size) : x->RS->Size);
else return Find(x->RS);
}
int main() {
for (;;) {
Clr();
if (!n) break;
for (unsigned i(1); i <= n; ++i) { Sum[i] = Sum[i - 1] + (a[i] = RDsg()); if (Sum[i] < Min) Min = Sum[i], Pos = i; }
if ((m = Sum[n]) <= 0) { printf("-1\n");continue; }
for (unsigned i(1); i <= n; ++i) { b[i] = a[(Pos + i > n) ? (Pos + i - n) : (Pos + i)]; }
for (unsigned i(1); i <= n; ++i) Sum[i] = Sum[i - 1] + b[i];
Root->ValL = Root->ValR = Sum[1], Root->Size = 1, Root->LS = Root->RS = NULL;
for (unsigned i(2); i <= n; ++i) A = Sum[i], Ans += Find(Root), Root = Insert(Root);
sort(Sum + 1, Sum + n + 1, greater<long long>()), Sum[n + 1] = 0x3f3f3f3f3f3f3f3f, Last = 1, Cnt = 1;
for (unsigned i(1); i <= n; ++i, ++Cnt) {
if (Sum[i] ^ Sum[i + 1]) {
Pos = Sum[i] % m, A = Sum[i] / m;
for (unsigned j(0); j < m; ++j) Ans += (Pls[j] - PCnt[j] * (A + ((Pos < j) ? 0 : 1))) * Cnt;
Pls[Pos] += Cnt * A, PCnt[Pos] += Cnt, Cnt = 0;
}
}
printf("%lld\n", Ans);
}
return Wild_Donkey;
}
但是仍然遗憾, 我的程序得了 100′, 但是是过题的三个人的最劣解, 而且严重低于平均, 在别人 1100+ms 的时候, 我跑了 1300+ms.
然后为了抢最优解, 我选择了树状数组, 然后以 715ms 过掉了此题, 堪称用更短的代码跑更快的常数的典范. (其实去掉缺省源, 我就是最短解)
int a[100005], m;
unsigned BIT[100005], InvSum[100005];
long long Sum[100005], TmpSum[100005], Min;
unsigned long long A, Pls[15], Ans;
unsigned n, Cnt, PCnt[15], Pos;
inline void Clr() {
memset(BIT, 0, (n + 1) << 2);
if ((m > 0) && (m <= 10)) memset(Pls, 0, m << 3), memset(PCnt, 0, m << 2);
n = RD(), Ans = 0, Min = 0x3f3f3f3f3f3f3f3f;
}
int main() {
for (Clr();n; Clr()) {
for (unsigned i(1); i <= n; ++i) { Sum[i] = Sum[i - 1] + (a[i] = RDsg()); if (Sum[i] < Min) Min = Sum[i], Pos = i; }
if (Sum[n] <= 0) { printf("-1\n");continue; }
for (unsigned i(1); i <= n; ++i) TmpSum[i] = Sum[i] = Sum[i - 1] + a[(Pos + i > n) ? (Pos + i - n) : (Pos + i)];
sort(Sum + 1, Sum + n + 1, greater<long long>());
for (unsigned i(1); i <= n; ++i) InvSum[i] = lower_bound(Sum + 1, Sum + n + 1, TmpSum[i], greater<long long>()) - Sum;
for (unsigned i(1); i <= n; ++i) {
for (unsigned j(InvSum[i] - 1); j; j -= Lowbit(j)) Ans += BIT[j];
for (unsigned j(InvSum[i]); j <= n; j += Lowbit(j)) ++BIT[j];
}
Sum[n + 1] = 0x3f3f3f3f3f3f3f3f, Cnt = 1, m = TmpSum[n];
for (unsigned i(1); i <= n; ++i, ++Cnt) {
if (Sum[i] ^ Sum[i + 1]) {
Pos = Sum[i] % m, A = Sum[i] / m;
for (unsigned j(0); j < m; ++j) Ans += (Pls[j] - PCnt[j] * (A + ((Pos < j) ? 0 : 1))) * Cnt;
Pls[Pos] += Cnt * A, PCnt[Pos] += Cnt, Cnt = 0;
}
}
printf("%llu\n", Ans);
}
return Wild_Donkey;
}
我愿称此题为最难, 难在它的题解简洁晦涩难懂, 难在它没有标程 (然后在仅仅过掉的三个人中, 有一个是贺的另一个人的, 直接给我笑吐了, 贺别人的跑得还没人家快). 所以我前后总共写了 5 篇代码, 占据了非常大的篇幅.
C
稍微转化一波发现是求所有本质不同的子串出现次数的平方和.
发现 n=1 的情况很好做, 只需要建 SAM, 定义 Cnt 为后缀树子树内的前缀节点数量, 然后求每个点 (Len−FailLen)Cnt2 之和即可.
当 n>1 时, 可以在线构造 GSAM, 然后对每个询问遍历后缀树, 同样能求出答案, 但是时间复杂度是 n∑L, 只能得 58′.
接下来考虑优化.
因为我们只要知道哪些点的 Cnt 或 Fail 改变了即可 (因为一个点的 L 一旦确定永不改变, 所以不用讨论).
对于 Fail 来说, 只有分裂的时候会修改, 所以需要讨论的点数和 L 有关. 而 Cnt 则是一个点改变引起整条链的 Cnt 值改变, 所以考虑树剖, 但是树剖不能在线维护, 所以现在有两条路: 离线树剖和 LCT 在线维护.
因为本题没有强制在线, 所以考虑树剖. 需要实现维护 (Len−FailLen)Cnt2, 则需要维护 Dif=Len−FailLen 的单点修改, Cnt 的区间加, Cnt2 的区间加, 记录每个字符串插入的时候的操作序列, 离线回答即可.
这个题的思路非常套路, 但是它的难点在代码.
unsigned m, n, A, B, C, D, t, Ans(0), Tmp(0), NofS;
unsigned CntE(0), CntD(0), Pos[100005];
char a[300005], NowC;
struct Edit {
unsigned Nid, Opt;
}E[1200005];
struct Seg {
Seg* LS, * RS;
unsigned long long DiCnt2, DiCnt, Di;
unsigned TagofPCnt;
}S[1200005], * CntS(S);
void PsDw(Seg* x) {
if (x->TagofPCnt) {
unsigned long long Sq(x->TagofPCnt * x->TagofPCnt);
(x->LS->TagofPCnt) += x->TagofPCnt, (x->RS->TagofPCnt) += x->TagofPCnt;
x->LS->DiCnt2 += ((x->LS->DiCnt << 1) * x->TagofPCnt) + Sq * x->LS->Di;
x->RS->DiCnt2 += ((x->RS->DiCnt << 1) * x->TagofPCnt) + Sq * x->RS->Di;
x->LS->DiCnt += x->LS->Di * x->TagofPCnt;
x->RS->DiCnt += x->RS->Di * x->TagofPCnt;
x->TagofPCnt = 0;
}
}
void PsUp(Seg* x) {
x->DiCnt2 = x->LS->DiCnt2 + x->RS->DiCnt2;
x->DiCnt = x->LS->DiCnt + x->RS->DiCnt;
x->Di = x->LS->Di + x->RS->Di;
}
void Build(Seg* x, unsigned L, unsigned R) {
if (L == R) return;
unsigned Mid((L + R) >> 1);
Build(x->LS = ++CntS, L, Mid), Build(x->RS = ++CntS, Mid + 1, R);
}
void ChgCnt(Seg* x, unsigned L, unsigned R) {
if ((A <= L) && (R <= B)) { x->DiCnt2 += (x->DiCnt << 1) + x->Di, x->DiCnt += x->Di, ++(x->TagofPCnt);return; }
unsigned Mid((L + R) >> 1);
PsDw(x);
if (A <= Mid) ChgCnt(x->LS, L, Mid);
if (Mid < B) ChgCnt(x->RS, Mid + 1, R);
PsUp(x);
}
void ChgDif(Seg* x, unsigned L, unsigned R) {
if (L == R) { x->DiCnt = x->TagofPCnt * B, x->DiCnt2 = x->TagofPCnt * x->DiCnt, x->Di = B;return; }
unsigned Mid((L + R) >> 1);
PsDw(x);
if (A <= Mid) ChgDif(x->LS, L, Mid);
else ChgDif(x->RS, Mid + 1, R);
PsUp(x);
}
struct Node {
Node* To[26], * Fail, * Son, * Bro, * Heavy, * Top;
unsigned Len, DFSr, Size;
}N[600005], * CntN(N), * Last(N);
void Add() {
register Node* Back(Last);
if (Back->To[NowC]) {
if (Back->To[NowC]->Len == Back->Len + 1) Last = Back->To[NowC];
else {
Node* Bfr(Back->To[NowC]);
*(Last = ++CntN) = *Bfr, Last->Len = Back->Len + 1, Bfr->Fail = Last;
E[++CntE].Nid = Bfr - N, E[CntE].Opt = Bfr->Len - Last->Len;
E[++CntE].Nid = Last - N, E[CntE].Opt = Last->Len - Last->Fail->Len;
while (Back && (Back->To[NowC] == Bfr)) Back->To[NowC] = Last, Back = Back->Fail;
}
return;
}
Last = ++CntN, Last->Len = Back->Len + 1;
while (Back && (!(Back->To[NowC]))) Back->To[NowC] = Last, Back = Back->Fail;
if (Back) {
if ((Back->To[NowC]->Len) ^ (Back->Len + 1)) {
Node* Bfr(Back->To[NowC]);
*(++CntN) = *Bfr, CntN->Len = Back->Len + 1, Bfr->Fail = Last->Fail = CntN;
E[++CntE].Nid = Bfr - N, E[CntE].Opt = Bfr->Len - CntN->Len;
E[++CntE].Nid = Last - N, E[CntE].Opt = Last->Len - CntN->Len;
E[++CntE].Nid = CntN - N, E[CntE].Opt = CntN->Len - CntN->Fail->Len;
while (Back && (Back->To[NowC] == Bfr)) Back->To[NowC] = CntN, Back = Back->Fail;
}
else Last->Fail = Back->To[NowC], E[++CntE].Nid = Last - N, E[CntE].Opt = Last->Len - Last->Fail->Len;
}
else Last->Fail = N, E[++CntE].Nid = Last - N, E[CntE].Opt = Last->Len;
}
void ChgAp(Node* x) {
while (x) A = x->Top->DFSr, B = x->DFSr, ChgCnt(S, 1, NofS), x = x->Top->Fail;
}
void PreDFS(Node* x) {
Node* Now(x->Son);
unsigned Mx(0);
x->Size = 1;
while (Now) {
PreDFS(Now);
x->Size += Now->Size;
if (Now->Size > Mx) x->Heavy = Now, Mx = Now->Size;
Now = Now->Bro;
}
return;
}
void DFS(Node* x) {
x->DFSr = ++CntD;
if (!(x->Heavy)) return;
Node* Now(x->Son);
x->Heavy->Top = x->Top, DFS(x->Heavy);
while (Now) {
if (Now != x->Heavy) { Now->Top = Now, DFS(Now); }
Now = Now->Bro;
}
return;
}
int main() {
n = RD();
for (unsigned i(1), j(1); i <= n; ++i, j = 1, Last = N) {
scanf("%s", a + 1);
while (a[j] < 'a') ++j;
while (a[j] >= 'a') NowC = a[j] -= 'a', Add(), a[j++] = 0, E[++CntE].Nid = Last - N, E[CntE].Opt = 0;
Pos[i] = CntE;
}
for (Node* i(N + 1); i <= CntN; ++i) i->Bro = i->Fail->Son, i->Fail->Son = i;
N->Top = N, PreDFS(N), DFS(N), NofS = CntN - N + 1, Build(S, 1, NofS);
for (unsigned i(1), j(1); i <= n; ++i) {
for (;j <= Pos[i]; ++j) {
if (E[j].Opt) A = N[E[j].Nid].DFSr, B = E[j].Opt, ChgDif(S, 1, NofS);
else ChgAp(N + E[j].Nid);
}
printf("%llu\n", S->DiCnt2);
}
return Wild_Donkey;
}
很遗憾拿了最劣解, 但是指针 SAM (尤指字符集大于等于 26 的 SAM) 必然是最劣解吧...
但是非常羞耻, 我一个弱智树剖写了一晚上.
D
貌似是第二简单的.
给一个 0/1 串 S, 求随机添加字符, 得到后缀 S 停止, 求长度期望.
先分析边界, 如果 S 只有一个 1, 则期望是 2, 这个值是 12+24+38+416+... 得到的, 转化为递归式 x=1+0+12x 即可解出, 其意义是这一位无论选什么, 都会贡献 1 的期望, 其中 12 的几率选 1, 长度是 0, 剩下的 12, 仍然是这个问题的递归, 所以期望就是自己本身.
设计状态 fi, 表示 S 的 (i,n] 作为后缀的期望长度, 或者说, fi 表示已经匹配了 S 的前缀 [1,i], 仍需要匹配多少能得到 S 的期望值. 容易知道边界的 fn=0.
设 Posi 为匹配 i 位后失配, 当前字符串的最长的和 S 的前缀匹配的后缀的长度, 这个可以在求 KMP 的 Nxt 数组的同时求出, 这时可以写出转移方程:
因为, i+1>i, Posi≤i 所以不方便直接 DP, 所以选择设 Difi 为 fi−1−fi, 通过递推式, 解出 Difi+1.
发现这个时候, j≤i, 所以这个时候是可以正序递推的, 加一个前缀和就可以优化到 O(n).
所求答案是 f0, 所以只需要将 Dif 求和就是答案.
不过还有生成函数的做法, 它非常好写, 而且非常容易扩展到一般的字符串, 而不仅仅是 0/1 串.
设 f(i) 是放了 i 个数, 刚好第一次得到 S 的概率, g(i) 是放了 i 个数, 还没有得到 S 的概率.
设 F(x) 和 G(x) 是 f(x) 和 g(x) 的生成函数.
因为 g(i) 表示的情况中, 再选第 i+1 个字符, 有且仅有两种情况, 即第 i+1 位得到 S 了, 和第 i+1 位没得到 S, 所以有式子:
对应到生成函数里就是:
对于 g(i), 也就是还没有出现 S 的状态, 如果这时在后面连续放一个 S 串, 一定能得到一个 S, 并且结束. 但是有可能会提前得到 S 而结束.
对于 g(i) 状态后面恰好放一整个 S 的情况, 它要求后面每一次加字符都恰好得到我们想要的, 所以这种理想状态的概率为 g(i)2n.
这时定义一个布尔数组 IsBd, 其中 IsBdi 表示 S 的前缀 [1,i] 是否和后缀 [n−i+1,n] 匹配.
因为 g(i) 涵盖了所有选择 i 个字符仍未得到 S 的情况, 所以 f(i+j)[IsBdj] 所表示的所有情况都应该被 g(i)2n 所包含. 但是显然在 i+j 就已经得到 S 的情况不管本来打算在 (i+j,i+n] 放什么都无所谓了, 但是我们之前规定 i 后面要放整个 S, 所以相当于得到 S 后仍然强制放 n−j 个我们想要的字符, 这就需要在原本的 fi+j 上除以 2n−j 得到它在 g(i)2n.
仍然对应到生成函数:
化简得到:
因为本题是求期望, 所以考虑概率和期望的关系, 发现概率生成函数 F(x) 的导数 F′(x) 乘一个 x 就是期望的生成函数, 因为:
这时, 如果将 x 取 1, 发现 F′(1)=∑iai 即为所求答案.
将 i 代入之前的式子:
发现答案转化为 G(1), 然后回到刚刚的式子:
最后只要求出 F(1) 就可以了.
然后得出结论:
所以只要从 i=n 不断跳 Nxti, 并且对 2i 求和即可. 这个做法可以推广到任意字符集大小的问题.
unsigned Mod(1000000007);
unsigned Nxt[1000005], f[1000005], Bin[1000005], m, n(0), Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
char a[1000005];
int main() {
fread(a + 1, 1, 1000002, stdin);
Nxt[1] = 0, Bin[0] = 1;
for (register unsigned i(2), j(1); a[i] >= '0'; ++i) {
n = i;
j = i - 1;
while (j && (a[Nxt[j] + 1] ^ a[i])) {
j = Nxt[j];
}
if(!j) {Nxt[i] = 0; continue;}
Nxt[i] = Nxt[j] + 1;
}
f[n] = 0;
for (register unsigned i(1); i <= n; ++i) {
Bin[i] = (Bin[i - 1] << 1);
if(Bin[i] >= Mod) Bin[i] -= Mod;
}
register unsigned i(n);
while (i) {
Ans += Bin[i];
if(Ans >= Mod) Ans -= Mod;
i = Nxt[i];
}
printf("%u\n", Ans);
return Wild_Donkey;
}
所以接下来是本题的加强版;
CTSC2006
给一个字符集大小 w, 给 t 个序列 Si, 表示 t 个询问.
询问每次随机选择字符集中一个字符加在末尾, 得到 Si 就退出, 选择的字符连成的串长期望的后 4 位.
发现每个询问的答案, 可以直接由上一题推广而来:
unsigned a[100005], Nxt[100005], Pow[100005], m, n, w;
unsigned Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
inline void Clr() {
n = RD(), Ans = 0;
}
signed main() {
w = RD() % 10000, t = RD(), Pow[0] = 1;
for (unsigned i(1); i <= 100000; ++i) Pow[i] = Pow[i - 1] * w % 10000;
for (unsigned T(1); T <= t; ++T) {
Clr();
for (unsigned i(1); i <= n; ++i) a[i] = RD();
for (unsigned i(1), j(0); i <= n; ++i, j = i - 1) {
while (j && (a[i] ^ a[Nxt[j] + 1])) j = Nxt[j];
Nxt[i] = j ? (Nxt[j] + 1) : 0;
}
while (n) { Ans += Pow[n]; if (Ans >= 10000) Ans -= 10000; n = Nxt[n]; }
printf("%04u\n", Ans);
}
system("pause");
return Wild_Donkey;
}
Day14: ACtion Movie
A
大模拟, 有 N 个苹果, M 个骨头, 需要 A 个苹果, B 个骨头.
需要 X 时间生产一个苹果, Y 时间生产一个骨头.
可以用 C 个苹果换 D 个骨头, 可以用 D 个骨头换 C 个苹果.
求得到至少 A 苹果, B 骨头的最短时间.
A,B,C,D≤1000
首先有个性质: 只要 N≥A+C 或 M≥B+D, 一定把多出来的苹果或骨头换成另一种.
然后是 N+C≤A 或 M+D≤B, 这时如果生产 C 个苹果比 D 个骨头时间短, 则生产 C 个苹果换成 D 个骨头代替直接生产骨头, 反之亦然.
对于整段之后的零头, 仍然要讨论, 比如现在 N+C>A, 但是 A−N 个苹果生产仍然不如生产 D 个骨头, 那就选择 D 个骨头换出 C 个苹果.
还要讨论一开始形如 A<N<A+C 的情况, 因为有时候, 拿 C 个苹果换到 D 个骨头, 然后生产 C+A−N 个苹果的方案更优.
unsigned a[10005], N, M, X, Y, m, n, Cnt(0), A, B, C, D, t, TmpB, TmpA, Ans(0), Tmp1(0), Tmp2(0), Tmp(0);
char b[10005];
int main() {
N = RD(), M = RD(), X = RD(), Y = RD(), A = RD(), B = RD(), C = RD(), D = RD();
if((N >= A) && (M >= B)) {
printf("0\n");
return 0;
}
if(N >= A) {
M += ((N - A) / C) * D;
if(M >= B) {
printf("0\n");
return 0;
}
Tmp = (N - A + C - 1) / C;
TmpB = M + Tmp * D;
if(TmpB >= B) Tmp1 = X * (A + Tmp * C - N);
else Tmp1 = X * (A + Tmp * C - N) + min(((B - TmpB + D - 1) / D) * C * X, Y * (B - TmpB));
Tmp2 = min(((B - M + D - 1) / D) * C * X, Y * (B - M));
Ans += min(Tmp1, Tmp2);
printf("%u\n", Ans);
return 0;
}
if(M >= B) {
N += ((M - B) / D) * C;
if(N >= A) {
printf("0\n");
return 0;
}
Tmp = (M - B + D - 1) / D;
TmpA = N + Tmp * C;
if(TmpA >= A) Tmp1 = Y * (B + Tmp * D - M);
else Tmp1 = Y * (B + Tmp * D - M) + min(((A - TmpA + C - 1) / C) * D * Y, X * (A - TmpA));
Tmp2 = min(((A - N + C - 1) / C) * D * Y, X * (A - N));
Ans += min(Tmp1, Tmp2);
printf("%u\n", Ans);
return 0;
}
TmpA = ((A - N) / C) * D * Y + X * (A - (((A - N) / C) * C) - N);
TmpB = ((B - M) / D) * C * X + Y * (B - (((B - M) / D) * D) - M);
Ans += min(min(((A - N + C - 1) / C) * D * Y, X * (A - N)), TmpA);
Ans += min(min(((B - M + D - 1) / D) * C * X, Y * (B - M)), TmpB);
printf("%u\n", Ans);
return Wild_Donkey;
}
B
给一个 1,2,3,...,n 的序列, 可以随意选择几位, 将它变成 x−1, 然后求异或和.
一共有 2n 种情况, 求这 2n 种情况得到的异或和中, ≥m 的情况数.
打表题, 打表发现, 无论 n 是多少, 最后前缀和中, [0,2⌊logn⌋+1) 每种数字出现次数相同.
所以对于 m, 求 2n(m+1)2⌊logn⌋+1=2n−⌊logn⌋−1(m+1) 即可, 快速幂解决.
const unsigned long long MOD(1000000007);
unsigned long long m, n, Cnt(0), N, Ans(0), Tmp(0), a[1005];
unsigned long long Power(unsigned long long y) {
register unsigned long long Tmpx(2), Final(1);
while (y) {
if(y & 1) {
Final = Final * Tmpx % MOD;
}
Tmpx = Tmpx * Tmpx % MOD;
y >>= 1;
}
return Final;
}
int main() {
Tmp = n = RD(), m = RD();
while (Tmp) {
++Cnt;
Tmp >>= 1;
}
N = ((unsigned long long)1 << Cnt) - 1;
m = min(N, m);
printf("%llu\n", ((1 + m) % MOD) * Power(n - Cnt) % MOD);
return Wild_Donkey;
}
D
构造数据卡贪心.
有 n 个数, 要求分成两个集合使得它们的和的差尽可能小.
需要 Hack 的算法: 降序排序, 将数字插入和较小的那个集合.
给定 n, m, 输出 n 个数, 分成两个集合差值最小是 m.
发现原算法可以在 n≤5 的时候给出正确答案.
原算法一定会使得最大的和二大的数字分到两个不同的集合中, 所以我们只要构造数据使得答案中最大的和二大的数字分到一个集合中即可.
G
一棵树, 两点之间连的是双向边, 也就是一共 2(n−1) 条有向边.
一条边可以被删除, 当且仅当它的终点不存在到达不是它的起点的点的出边.
发现一开始所有连向叶子的边都可以被删除, 删除连向叶子的边之后, 连向这些删除了的边的起点的边也可以删除, 所以 DFS 回溯过程中删除之前走的每一条边即可. 这样就删掉了所有父亲连向儿子的边.
然后发现这时连向根的边可以被删除, 删除这些边之后, 每一颗子树又变成了同样的子问题, 所以仍然是 DFS, 在搜索一个子树之前, 删除这个子树连向根的边即可.
unsigned a[10005], m, n, Cnt(0), C, D, t, Ans(0), Tmp(0);
struct Edge;
struct Node {
Edge *Fst;
Node *Fa;
}N[100005], *A, *B;
struct Edge {
Node *To;
Edge *Nxt;
}E[200005], *CntE(E);
void Link(Node *x, Node *y) {
(++CntE)->Nxt = x->Fst;
x->Fst = CntE;
CntE->To = y;
}
void DFS(Node *x) {
Edge *Sid(x->Fst);
while (Sid) {
if(Sid->To != x->Fa) {
Sid->To->Fa = x;
DFS(Sid->To);
printf("%u %u\n", x - N, Sid->To - N);
}
Sid = Sid->Nxt;
}
}
void DFS2 (Node *x) {
Edge *Sid(x->Fst);
while (Sid) {
if(Sid->To != x->Fa) {
printf("%u %u\n", Sid->To - N, x - N);
DFS2(Sid->To);
}
Sid = Sid->Nxt;
}
}
int main() {
n = RD();
for (register unsigned i(1); i < n; ++i) {
A = N + RD(), B = N + RD();
Link(A, B);
Link(B, A);
}
DFS(N + 1);
DFS2(N + 1);
return Wild_Donkey;
}
J
对一个序列执行一次操作, 使得前 k 个数接到第 n 个数后面.
然后对序列进行合并, 规则是两个相邻的数字 x, y 合成一个数 x−y, 每轮之后对新的数组重复操作, 直到数组只剩一个元素.
求合并到只剩一个元素的最大值.
使用倍增, ai,j 表示从 i 开始合并到 i+2i−1 的结果.
所以这个是类似 ST 表的思想, 需要 O(nlogn) 的空间预处理.
破环为链, 枚举每个起始位置, 这样就可以每次二进制分组, 暴力合并得到的长度为 logn 的序列即可.
遗憾的是, 虽然场切了核心思想, 但是下面这个细节却没有调出来, 否则就是场上唯一一个切 8 题的学生队伍了.
暴力合并时, 要注意不能使用直接合并的规则, 因为每个元素不是同时得到的, 所以一定是原序列较小的元素先合并, 所以答案应该是得到的序列从左到右交替加减得到的结果.
long long a[200005][20], m, n, Cnt(0), A, B, C, D, t, Ans(-0x3f3f3f3f3f3f3f3f), Tmp[100005], Bin[200005], Log[200005];
long long Force() {
register long long All(0);
for (register unsigned i(1); i <= Cnt; ++i) {
if(i & 1) {
All += Tmp[i];
} else {
All -= Tmp[i];
}
}
return All;
}
int main() {
m = RD(), n = m << 1;
for (register unsigned i(1), j(0); i <= n; i <<= 1, ++j) {
Bin[j] = i, Log[i] = j;
}
for (register unsigned i(1); i <= n; ++i) {
Log[i] = max(Log[i - 1], Log[i]);
}
for (register unsigned i(1); i <= m; ++i) {
a[i + m][0] = a[i][0] = RD();
}
for (register unsigned j(1); j <= Log[m]; ++j) {
for (register unsigned i(1); i + Bin[j] <= n; ++i) {
a[i][j] = a[i][j - 1] - a[i + Bin[j - 1]][j - 1];
}
}
for (register unsigned i(1); i <= m; ++i) {
Cnt = 0;
register unsigned Len(0);
for (register unsigned j(Log[m]); j < 0x3f3f3f3f; --j) {
if(Len + Bin[j] <= m) {
Tmp[++Cnt] = a[i + Len][j];
Len += Bin[j];
}
}
Ans = max(Force(), Ans);
}
printf("%lld\n", Ans);
return Wild_Donkey;
}
L
给一个六边形网格, 每次将一个连通块涂成红色或蓝色, 求整个变成蓝色的最少涂色数量.
搜索, 得到每个连通块的相邻关系, 每个连通块作为一个点, 和与它相邻的点连边, 得到一个二分图, 这时二分图一定是一棵树, 这是因为六边形网格的特殊性不存在环.
发现每次做染色操作相当于以某个连通块所在的点为根, 将树从上面减少一层, 所以整个图变成统一颜色的操作数是树高, 所以我们要求出树高最小的根.
这个最小的树高即为直径的二分之一向上取整. (直径定义为最长链的边数)
特别地, 有可能最后整个图变成红色, 在直径为奇数的时候可以通过选择合适的直径中点作为根来控制最终颜色, 操作次数也不会改变.
特判直径为偶数的时候, 这时如果直径中点是蓝色, 直径的一半是偶数, 答案不变, 直径一半是奇数, 答案增加 1; 如果中点是红色, 直径一半是偶数, 答案增加 1, 否则答案不变.
M
一条长 L 的路, 路上有 n 个消防局, 可以在没有消防局的整点上修建筑. 修 m 个建筑, 使得所有建筑到最近的消防局的距离的最大值最小.
显然是二分答案题, 二分最大距离 x, 在每个消防局周围 x 范围内放满建筑, 看是否放够了 m 个即可.
unsigned a[100005], m, n, Cnt(0), A, B, C, D, L, t, Ans(0), Tmp(0);
char Judge (unsigned x) {
register unsigned Now(0);
a[n + 1] = L + x + 1;
for (register unsigned i(1); i <= n; ++i) {
Now += min(a[i] - a[i - 1] - 1, x);
if(a[i + 1] - a[i] - 1 > x) {
Now += min(a[i + 1] - a[i] - 1 - x, x);
}
}
return Now >= m;
}
int main() {
n = RD(), m = RD(), L = RD();
for (register unsigned i(1); i <= n; ++i) {
a[i] = RD();
}
a[0] = 0;
sort(a + 1, a + n + 1);
register l(1), r(L), Mid;
while (l < r) {
Mid = ((l + r) >> 1);
if(Judge(Mid)) {
r = Mid;
} else {
l = Mid + 1;
}
}
printf("%u\n", l);
return Wild_Donkey;
}
N
轮廓线长度, 直接从左到右扫描即可.
unsigned a[10005], m, n, Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
char b[10005];
inline void Clr() {}
int main() {
Ans = n = RD();
for (register unsigned i(1); i <= n; ++i) {
a[i] = RD();
}
++n;
for (register unsigned i(1); i <= n; ++i) {
if(a[i] > a[i - 1]) {
Ans += a[i] - a[i - 1];
} else {
Ans += a[i - 1] - a[i];
}
}
printf("%u\n", Ans);
return Wild_Donkey;
}
O
构造一个长度为 m 的数, 各位和为 n.
不能有前导零, n=0 时只有 m=1 时有解, 为 0.
总和除以长度向下取整得到每一位的数, 然后将余数从高到低补上即可.
unsigned m, n, Base, Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
inline void Clr() {}
int main() {
n = RD(), m = RD();
if(!n) {
if(m > 1) {
printf("-1\n");
return 0;
} else {
printf("0\n");
return 0;
}
}
Base = n / m;
if(Base > 9) {
printf("-1\n");
return 0;
}
if((Base == 9) && (Base * m < n)) {
printf("-1\n");
return 0;
}
for (register unsigned i(1); i <= n - (Base * m); ++i) {
printf("%u", Base + 1);
}
for (register unsigned i(n - (Base * m) + 1); i <= m; ++i) {
printf("%u", Base);
}
putchar('\n');
return Wild_Donkey;
}
P
翻转字符串, 如果首字母大写, 则反转后的首字母大写, 也就是原串末字符大写.
按空格分割每个字符串输入, 判断首字符, 打 Tag, 将所有字符转化为小写, 翻转, 然后输出时判断 Tag 将首字符大写即可.
unsigned Pos[3005], n(3000), Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
char a[3005], b[3005], Tag[3005];
int main() {
fread(a + 1, 1, 3002, stdin);
while (a[n] < 'A') {
--n;
}
Pos[0] = 0;
for (register unsigned i(1); i <= n; ++i) {
if(a[i] < 'A') {
Pos[++Cnt] = i;
}
if(a[i] >= 'A' && a[i] < 'a') {
Tag[Cnt] = 1;
a[i] += 'a' - 'A';
}
}
Pos[++Cnt] = n + 1;
for (register unsigned i(0); i < Cnt; ++i) {
if(Tag[i]) {
a[Pos[i + 1] - 1] -= 'a' - 'A';
}
}
for (register unsigned i(n); i; --i) {
putchar(a[i]);
}
putchar('\n');
return Wild_Donkey;
}
Day15: 连通性
强连通分量
过水已隐藏
Tip: Tarjan 找到强连通分量的顺序反转后是得到的 DAG 的拓扑序, 原因是一个点被弹出时, 它连向的点一定也被弹出了, 所以一个强连通分量被弹出时, 所有拓扑序应该比它大的点都被弹出了.
NOIp2009
n 个点, m 条单/双向边, 从点 1 到点 n, 在路径上取一个点 A, 然后在这个点之后再取一个点 B, 求 B−A 的最大值.
缩点, 处理每个强连通分量的最大值和最小值, 然后拓扑排序 + DP, 求出从 1 到一个点路径上最小值和从一个点到 n 路径上最大值. 答案即为这两个值差最大的点的差值.
也可以只搜索一次, 选择不记录一个点到 n 的最大值, 可以维护 1 到每个点的答案, 每次使用入边起点的答案更新自己的答案, 然后用自己的最大值和路径最小值讨论 B 取在自己的强连通分量中的情况.
unsigned m, n;
unsigned A, B, C, D, Top;
unsigned Cnt(0), Tmp(0);
struct SCC;
struct Node;
struct SCCE {
SCC* To;
SCCE* Nxt;
}SE[1000005], * CntSE(SE);
struct SCC {
SCCE* Fst;
unsigned Max, Min, Ans;
}S[100005], * CntS(S);
struct Edge {
Node* To;
Edge* Nxt;
}E[1000005], * CntE(E);
struct Node {
Edge* Fst;
SCC* Bel;
unsigned Val, DFSr, Low;
char InStk;
}N[100005], * Stack[100005];
void Add(Node* x) {
Edge* Sid(x->Fst);
while (Sid) {
if (Sid->To->Bel) {
(++CntSE)->Nxt = x->Bel->Fst;
x->Bel->Fst = CntSE;
CntSE->To = Sid->To->Bel;
}
Sid = Sid->Nxt;
}
}
void DFS(Node* x) {
x->Low = x->DFSr = ++Cnt, Stack[++Top] = x, x->InStk = 1;
Edge* Sid(x->Fst);
while (Sid) {
if (Sid->To->DFSr) {
if (Sid->To->InStk) x->Low = min(x->Low, Sid->To->Low);
}
else {
DFS(Sid->To);
x->Low = min(x->Low, Sid->To->Low);
}
Sid = Sid->Nxt;
}
if (x->Low == x->DFSr) {
(++CntS)->Min = 0x3f3f3f3f;
while (Stack[Top] != x) {
CntS->Max = max(CntS->Max, Stack[Top]->Val);
CntS->Min = min(CntS->Min, Stack[Top]->Val);
Stack[Top]->InStk = 0, Stack[Top--]->Bel = CntS;
}
CntS->Max = max(CntS->Max, Stack[Top]->Val);
CntS->Min = min(CntS->Min, Stack[Top]->Val);
Stack[Top]->InStk = 0, Stack[Top--]->Bel = CntS;
}
}
signed main() {
n = RD(), m = RD();
for (unsigned i(1); i <= n; ++i) N[i].Val = RD();
for (unsigned i(0); i < m; ++i) {
A = RD(), B = RD(), C = RD();
(++CntE)->Nxt = N[A].Fst, N[A].Fst = CntE, CntE->To = N + B;
if (C & 2)
(++CntE)->Nxt = N[B].Fst, N[B].Fst = CntE, CntE->To = N + A;
}
DFS(N + 1);
for (unsigned i(1); i <= n; ++i) if (N[i].Bel) Add(N + i);
for (SCC* i(CntS); i > S;--i) {
i->Ans = max(i->Ans, i->Max - i->Min);
SCCE* Sid(i->Fst);
while (Sid) {
Sid->To->Min = min(i->Min, Sid->To->Min);
Sid->To->Ans = max(i->Ans, Sid->To->Ans);
Sid = Sid->Nxt;
}
}
printf("%u\n", N[n].Bel->Ans);
return Wild_Donkey;
}
CF1137C
n 个点的有向图, 每周期 d 天, 每个点的博物馆每周开放固定的天, 一开始在点 1, 每天沿着有向边走到下一个点, 如果无限时间最多可以参观多少博物馆.
将每个点差分成 d 个点, 分别表示每一天, 感性理解原来的强连通分量拆点之后, 新的点不是强连通就是不连通, 原来不强连通的点拆点后一定也不强连通.
这时每个点是否开放可以确定, 与时间无关. 所以缩强连通分量, 统计每个分量有多少个不同的城市的开放状态, 在 DAG 上从 1−1 点所在的分量跑 DP 即可.
unsigned m, n, p, M, Top(0), Top2;
unsigned A, B, C, D, t;
unsigned Cnt(0), Num[100005], Ans(0), Tmp(0);
char InAva[105];
struct SCC;
struct SEdge {
SCC* To;
SEdge* Nxt;
}SE[5000005], * CntSE(SE);
struct SCC{
SEdge* Fst;
unsigned f, City;
}S[5000005], * CntS(S);
struct Node;
struct Edge {
Node* To;
Edge* Nxt;
}E[5000005], * CntE(E);
struct Node {
Edge* Fst;
SCC* Bel;
unsigned DFSr, Low;
char Ava, InS;
}N[5000055], * Stack[5000005];
inline void Link(Node* x) {
Edge* Sid(x->Fst);
while (Sid) {
if((Sid->To->Bel) && (Sid->To->Bel != CntS))
(++CntSE)->Nxt = CntS->Fst, CntS->Fst = CntSE, CntSE->To = Sid->To->Bel;
Sid = Sid->Nxt;
}
}
inline void Tarjan(Node* x) {
x->Low = x->DFSr = ++Cnt, Stack[++Top] = x, x->InS = 1;
Edge* Sid(x->Fst);
while (Sid) {
if(!(Sid->To->DFSr)) Tarjan(Sid->To), x->Low = min(x->Low, Sid->To->Low);
else if(Sid->To->InS) x->Low = min(x->Low, Sid->To->Low);
Sid = Sid->Nxt;
}
if(x->Low == x->DFSr) {
(++CntS), Top2 = Top, Ans = 0;
do if ((Stack[Top2]->Ava) && (!(Num[(Stack[Top2] - N - 1) / p]++))) ++Ans;
while (Stack[Top2--] != x);
CntS->City = Ans;
while (Top ^ Top2) {
if (Stack[Top]->Ava) --Num[(Stack[Top] - N - 1) / p];
Stack[Top]->Bel = CntS, Stack[Top]->InS = 0, Link(Stack[Top--]);
}
}
}
signed main() {
n = RD(), m = RD(), p = RD();
for (unsigned i(1); i <= m; ++i) {
A = RD(), B = RD();
for (unsigned j(1); j < p; ++j)
(++CntE)->Nxt = N[(A * p) + j].Fst, N[(A * p) + j].Fst = CntE, CntE->To = N + (B * p) + j + 1;
(++CntE)->Nxt = N[(A * p) + p].Fst, N[(A * p) + p].Fst = CntE, CntE->To = N + (B * p) + 1;
}
for (unsigned i(1); i <= n; ++i) {
scanf("%s", InAva + 1);
for (unsigned j(1); j <= p; ++j)
N[(i * p) + j].Ava = InAva[j] - '0';
}
Tarjan(N + p + 1), Ans = 0, CntS->f = CntS->City;
for (SCC* i(CntS); i > S; --i) {
SEdge* Sid(i->Fst);
Ans = max(i->f, Ans);
while (Sid) {
Sid->To->f = max(Sid->To->f, i->f + Sid->To->City);
Sid = Sid->Nxt;
}
}
printf("%u\n", Ans);
return Wild_Donkey;
}
这个题卡栈空间, 在洛谷讨论区老哥的指导下, 开 inline 过掉此题, 有时候爆栈是 RE, 有时候是 MLE 要注意. 我们还学到一个道理: inline 既能用来卡常, 又能用来卡空.
双连通
emm, 关于做题时需要的性质, 这里有全网首个严格证明.
边双连通
连通无向图缩点后得到一棵树, 树边称作 "桥".
双连通转强连通
给一个边双连通图, 要求将边定向, 得到一个强连通图.
只要在原图上 DFS, 每条边方向就是第一次访问它的时候的方向.
证明正确性, 上面方法得到的有向图一定是一棵树边指向儿子的树和一些非树边. 假设最后不是强连通图, 则一定存在至少一个子树是一个强连通分量, 这时不存在边从子树连出, 所以这时子树父亲连到该子树的边在原图上就是一个桥, 但显然和双连通图的定义相悖. 因此算法正确.
缩点
可以将无向图以上述方式定向, 然后求强连通分量, 这时的强连通分量就是边双连通分量.
CEOI2017
给一个无向图, 需要给边定向使得 q 个点对 (Fri,Toi) 满足可以从 Fri 到达 Toi, 数据保证有解, 可能有重边或自环, 不保证图连通.
一条边有三种情况, 分别是正向, 反向和不定向, 如果确定一条边的方向, 输出这个答案.
既然边双连通分量可以定向成强连通分量, 这时必然先定向成强连通分量, 所以直接 Tarjan 缩边双.
因为强连通分量的所有边同时取反后仍然强连通, 所以所有边双内的边都可以直接取 B, 然后讨论树边的方向.
这个题, 我第一次使用了树链剖分对每个约束进行区间修改, 复杂度 O(n+mlog2n).
unsigned M, m, n, q;
unsigned AskFr, AskTo, C, D, t, Top(0);
unsigned Cnt(0), Ans(0), Tmp(0);
char Goal(0);
struct Seg {
Seg* LS, * RS;
char Val;
}S[200005], * CntS(S);
struct Node;
struct Edge {
Node* To;
Edge* Nxt;
char ToPr;
}E[200005];
struct BCC {
BCC* Son, * Fa[20], * Bro, * Top, * Heavy;
Edge* FaTo;
unsigned DFSr, Dep, Size;
}B[100005], * SortByDFS[100005], * CntB(B), * DoFr, * DoTo, * DoLCA;
struct Node {
Edge* Fst;
BCC* Bel;
unsigned DFSr, Low;
char InStack;
}N[100005], * Stack[100005];
void Link(Node* x) {
Edge* Sid(x->Fst);
while (Sid) {
if (Sid->To->Bel) {
if (Sid->To->Bel != x->Bel) {
Sid->To->Bel->Bro = x->Bel->Son;
x->Bel->Son = Sid->To->Bel;
Sid->To->Bel->Fa[0] = x->Bel;
Sid->To->Bel->FaTo = Sid;
}
}
Sid = Sid->Nxt;
}
return;
}
void PushDown(Seg* x) { if (x->Val) x->LS->Val = x->RS->Val = x->Val, x->Val = 0; }
void Build(Seg* x, unsigned L, unsigned R) {
if (L == R) return;
unsigned Mid((L + R) >> 1);
Build(x->LS = ++CntS, L, Mid), Build(x->RS = ++CntS, Mid + 1, R);
}
void Change(Seg* x, unsigned L, unsigned R) {
if ((C <= L) && (R <= D)) { x->Val = Goal;return; }
unsigned Mid((L + R) >> 1); PushDown(x);
if (C <= Mid) Change(x->LS, L, Mid);
if (D > Mid) Change(x->RS, Mid + 1, R);
}
void Print(Seg* x, unsigned L, unsigned R) {
if (L == R) { if (SortByDFS[L]->FaTo) SortByDFS[L]->FaTo->ToPr = x->Val;return; }
unsigned Mid((L + R) >> 1); PushDown(x);
Print(x->LS, L, Mid), Print(x->RS, Mid + 1, R);
}
void DFS(Node* x, Edge* No) {
x->DFSr = x->Low = ++Cnt, Stack[++Top] = x, x->InStack = 1;
Edge* Sid(x->Fst);
while (Sid) {
if (Sid != No) {
if (Sid->To->DFSr) { if (Sid->To->InStack) x->Low = min(x->Low, Sid->To->Low); }
else DFS(Sid->To, E + ((Sid - E) ^ 1)), x->Low = min(x->Low, Sid->To->Low);
}
Sid = Sid->Nxt;
}
if (x->DFSr == x->Low) {
++CntB;
while (Stack[Top] != x) {
Stack[Top]->Bel = CntB, Link(Stack[Top]), Stack[Top--]->InStack = 0;
}
Stack[Top]->Bel = CntB, Link(Stack[Top]), Stack[Top--]->InStack = 0;
}
}
void PreDFSB(BCC* x) {
BCC* Now(x->Son);
unsigned MaxSz(0);
x->Size = 1;
while (Now) {
for (char i(0); Now->Fa[i]; ++i) Now->Fa[i + 1] = Now->Fa[i]->Fa[i];
Now->Dep = x->Dep + 1, PreDFSB(Now), x->Size += Now->Size;
if (MaxSz < Now->Size) x->Heavy = Now, MaxSz = Now->Size;
Now = Now->Bro;
}
return;
}
void DFSB(BCC* x) {
BCC* Now(x->Son);
x->DFSr = ++Cnt, SortByDFS[Cnt] = x;
if (!(x->Heavy)) return;
x->Heavy->Top = x->Top, DFSB(x->Heavy);
while (Now) {
if (Now != x->Heavy) Now->Top = Now, DFSB(Now);
Now = Now->Bro;
}
return;
}
void LCA(BCC* x, BCC* y) {
if (x->Dep < y->Dep) swap(x, y);
for (char i(17); ~i; --i) if ((x->Fa[i]) && (x->Fa[i]->Dep >= y->Dep)) x = x->Fa[i];
if (x == y) { DoLCA = x;return; }
for (char i(17); ~i; --i) if ((x->Fa[i]) && (x->Fa[i] != y->Fa[i])) x = x->Fa[i], y = y->Fa[i];
DoLCA = x->Fa[0];
}
signed main() {
n = RD(), m = RD(), M = m << 1;
for (unsigned i(0); i < M; i += 2) {
C = RD(), D = RD();
E[i].Nxt = N[C].Fst, N[C].Fst = E + i, E[i].To = N + D;
E[i ^ 1].Nxt = N[D].Fst, N[D].Fst = E + (i ^ 1), E[i ^ 1].To = N + C;
}
for (unsigned i(1); i <= n; ++i) if (!(N[i].DFSr)) DFS(N + i, NULL);
Cnt = 0;
for (BCC* i(CntB); i > B; --i) if (!(i->DFSr))
i->Dep = 1, PreDFSB(i), i->Top = i, DFSB(i);
Build(S, 1, Cnt), q = RD();
for (unsigned i(1); i <= q; ++i) {
DoFr = N[RD()].Bel, DoTo = N[RD()].Bel;
if (DoFr == DoTo) continue;
LCA(DoFr, DoTo), Goal = 'L';
while (DoFr->Top != DoLCA->Top)
C = DoFr->Top->DFSr, D = DoFr->DFSr, Change(S, 1, Cnt), DoFr = DoFr->Top->Fa[0];
if (DoFr != DoLCA) C = DoLCA->DFSr + 1, D = DoFr->DFSr, Change(S, 1, Cnt);
Goal = 'R';
while (DoTo->Top != DoLCA->Top)
C = DoTo->Top->DFSr, D = DoTo->DFSr, Change(S, 1, Cnt), DoTo = DoTo->Top->Fa[0];
if (DoTo != DoLCA) C = DoLCA->DFSr + 1, D = DoTo->DFSr, Change(S, 1, Cnt);
}
Print(S, 1, Cnt);
for (unsigned i(0); i < M; i += 2) {
if (E[i].ToPr) { putchar(E[i].ToPr); continue; }
if (E[i ^ 1].ToPr) putchar((E[i ^ 1].ToPr ^ 'L') ? 'L' : 'R');
else putchar('B');
}
putchar('\n');
return Wild_Donkey;
}
学过树链剖分的都知道, 树链剖分本来就能用来求 LCA, 在这个基础上用倍增求 LCA 无疑是非常憨的举动, 于是放弃了使用倍增求 LCA.
unsigned M, m, n, q;
unsigned AskFr, AskTo, C, D, t, Top(0);
unsigned Cnt(0), Ans(0), Tmp(0);
char Goal(0);
struct Seg {
Seg* LS, * RS;
char Val;
}S[200005], * CntS(S);
struct Node;
struct Edge {
Node* To;
Edge* Nxt;
char ToPr;
}E[200005];
struct BCC {
BCC* Son, * Fa, * Bro, * Top, * Heavy;
Edge* FaTo;
unsigned DFSr, Dep, Size;
}B[100005], * SortByDFS[100005], * CntB(B), * DoFr, * DoTo;
struct Node {
Edge* Fst;
BCC* Bel;
unsigned DFSr, Low;
char InStack;
}N[100005], * Stack[100005];
void Link(Node* x) {
Edge* Sid(x->Fst);
while (Sid) {
if (Sid->To->Bel) {
if (Sid->To->Bel != x->Bel) {
Sid->To->Bel->Bro = x->Bel->Son;
x->Bel->Son = Sid->To->Bel;
Sid->To->Bel->Fa = x->Bel;
Sid->To->Bel->FaTo = Sid;
}
}
Sid = Sid->Nxt;
}
return;
}
void PushDown(Seg* x) { if (x->Val) x->LS->Val = x->RS->Val = x->Val, x->Val = 0; }
void Build(Seg* x, unsigned L, unsigned R) {
if (L == R) return;
unsigned Mid((L + R) >> 1);
Build(x->LS = ++CntS, L, Mid), Build(x->RS = ++CntS, Mid + 1, R);
}
void Change(Seg* x, unsigned L, unsigned R) {
if ((C <= L) && (R <= D)) { x->Val = Goal;return; }
unsigned Mid((L + R) >> 1); PushDown(x);
if (C <= Mid) Change(x->LS, L, Mid);
if (D > Mid) Change(x->RS, Mid + 1, R);
}
void Print(Seg* x, unsigned L, unsigned R) {
if (L == R) { if (SortByDFS[L]->FaTo) SortByDFS[L]->FaTo->ToPr = x->Val;return; }
unsigned Mid((L + R) >> 1); PushDown(x);
Print(x->LS, L, Mid), Print(x->RS, Mid + 1, R);
}
void DFS(Node* x, Edge* No) {
x->DFSr = x->Low = ++Cnt, Stack[++Top] = x, x->InStack = 1;
Edge* Sid(x->Fst);
while (Sid) {
if (Sid != No) {
if (Sid->To->DFSr) { if (Sid->To->InStack) x->Low = min(x->Low, Sid->To->Low); }
else DFS(Sid->To, E + ((Sid - E) ^ 1)), x->Low = min(x->Low, Sid->To->Low);
}
Sid = Sid->Nxt;
}
if (x->DFSr == x->Low) {
++CntB;
while (Stack[Top] != x) {
Stack[Top]->Bel = CntB, Link(Stack[Top]), Stack[Top--]->InStack = 0;
}
Stack[Top]->Bel = CntB, Link(Stack[Top]), Stack[Top--]->InStack = 0;
}
}
void PreDFSB(BCC* x) {
BCC* Now(x->Son);
unsigned MaxSz(0);
x->Size = 1;
while (Now) {
Now->Dep = x->Dep + 1, PreDFSB(Now), x->Size += Now->Size;
if (MaxSz < Now->Size) x->Heavy = Now, MaxSz = Now->Size;
Now = Now->Bro;
}
return;
}
void DFSB(BCC* x) {
BCC* Now(x->Son);
x->DFSr = ++Cnt, SortByDFS[Cnt] = x;
if (!(x->Heavy)) return;
x->Heavy->Top = x->Top, DFSB(x->Heavy);
while (Now) {
if (Now != x->Heavy) Now->Top = Now, DFSB(Now);
Now = Now->Bro;
}
return;
}
signed main() {
n = RD(), m = RD(), M = m << 1;
for (unsigned i(0); i < M; i += 2) {
C = RD(), D = RD();
E[i].Nxt = N[C].Fst, N[C].Fst = E + i, E[i].To = N + D;
E[i ^ 1].Nxt = N[D].Fst, N[D].Fst = E + (i ^ 1), E[i ^ 1].To = N + C;
}
for (unsigned i(1); i <= n; ++i) if (!(N[i].DFSr)) DFS(N + i, NULL);
Cnt = 0;
for (BCC* i(CntB); i > B; --i) if (!(i->DFSr))
i->Dep = 1, PreDFSB(i), i->Top = i, DFSB(i);
Build(S, 1, Cnt), q = RD();
for (unsigned i(1); i <= q; ++i) {
DoFr = N[RD()].Bel, DoTo = N[RD()].Bel;
if (DoFr == DoTo) continue;
while (DoFr->Top != DoTo->Top) {
if (DoFr->Top->Dep > DoTo->Top->Dep) {
Goal = 'L', C = DoFr->Top->DFSr, D = DoFr->DFSr, Change(S, 1, Cnt);
DoFr = DoFr->Top->Fa;
}
else {
Goal = 'R', C = DoTo->Top->DFSr, D = DoTo->DFSr, Change(S, 1, Cnt);
DoTo = DoTo->Top->Fa;
}
}
if (DoFr != DoTo) {
if (DoFr->Dep > DoTo->Dep) Goal = 'L', C = DoTo->DFSr + 1, D = DoFr->DFSr, Change(S, 1, Cnt);
else Goal = 'R', C = DoFr->DFSr + 1, D = DoTo->DFSr, Change(S, 1, Cnt);
}
}
Print(S, 1, Cnt);
for (unsigned i(0); i < M; i += 2) {
if (E[i].ToPr) { putchar(E[i].ToPr); continue; }
if (E[i ^ 1].ToPr) putchar((E[i ^ 1].ToPr ^ 'L') ? 'L' : 'R');
else putchar('B');
}
putchar('\n');
return Wild_Donkey;
}
能不能拒绝树剖? 答案是肯定的. 在缩点后得到的树上打标记, 然后差分, 得到每条边向上/下经过次数, 根据这个值的正负给桥定向.
unsigned M, m, n, q;
unsigned AskFr, AskTo, C, D, t, Top(0);
unsigned Cnt(0), Ans(0), Tmp(0);
char Goal(0);
struct Node;
struct Edge {
Node* To;
Edge* Nxt;
char ToPr;
}E[200005];
struct BCC {
BCC* Son, * Fa, * Bro;
Edge* FaTo;
int Dif;
char Vis;
}B[100005], * CntB(B), * DoFr, * DoTo;
struct Node {
Edge* Fst;
BCC* Bel;
unsigned DFSr, Low;
char InStack;
}N[100005], * Stack[100005];
void Link(Node* x) {
Edge* Sid(x->Fst);
while (Sid) {
if (Sid->To->Bel) {
if (Sid->To->Bel != x->Bel) {
Sid->To->Bel->Bro = x->Bel->Son;
x->Bel->Son = Sid->To->Bel;
Sid->To->Bel->Fa = x->Bel;
Sid->To->Bel->FaTo = Sid;
}
}
Sid = Sid->Nxt;
}
return;
}
void DFS(Node* x, Edge* No) {
x->DFSr = x->Low = ++Cnt, Stack[++Top] = x, x->InStack = 1;
Edge* Sid(x->Fst);
while (Sid) {
if (Sid != No) {
if (Sid->To->DFSr) { if (Sid->To->InStack) x->Low = min(x->Low, Sid->To->Low); }
else DFS(Sid->To, E + ((Sid - E) ^ 1)), x->Low = min(x->Low, Sid->To->Low);
}
Sid = Sid->Nxt;
}
if (x->DFSr == x->Low) {
++CntB;
while (Stack[Top] != x) {
Stack[Top]->Bel = CntB, Link(Stack[Top]), Stack[Top--]->InStack = 0;
}
Stack[Top]->Bel = CntB, Link(Stack[Top]), Stack[Top--]->InStack = 0;
}
}
void DFSB(BCC* x) {
BCC* Now(x->Son);
x->Vis = 1;
while (Now) {
DFSB(Now), x->Dif += Now->Dif;
Now = Now->Bro;
}
if (x->Dif < 0) x->FaTo->ToPr = 'R';
if (x->Dif > 0) x->FaTo->ToPr = 'L';
return;
}
signed main() {
n = RD(), m = RD(), M = m << 1;
for (unsigned i(0); i < M; i += 2) {
C = RD(), D = RD();
E[i].Nxt = N[C].Fst, N[C].Fst = E + i, E[i].To = N + D;
E[i ^ 1].Nxt = N[D].Fst, N[D].Fst = E + (i ^ 1), E[i ^ 1].To = N + C;
}
for (unsigned i(1); i <= n; ++i) if (!(N[i].DFSr)) DFS(N + i, NULL);
q = RD();
for (unsigned i(1); i <= q; ++i) ++(N[RD()].Bel->Dif), --(N[RD()].Bel->Dif);
for (BCC* i(CntB); i > B; --i) if (!(i->Vis)) DFSB(i);
for (unsigned i(0); i < M; i += 2) {
if (E[i].ToPr) { putchar(E[i].ToPr); continue; }
if (E[i ^ 1].ToPr) putchar((E[i ^ 1].ToPr ^ 'L') ? 'L' : 'R');
else putchar('B');
}
putchar('\n');
return Wild_Donkey;
}
ICPC2019WF
想当年这道题被选为校内 ACM 赛前训练,结果是历城二中 57 级全灭,全场三个队,只有有一个队有分,并且只有一道题,非常惨烈,今天重新审视这道题,发现当时水平确实太低。
这题题意比较绕,场上对题意也是一知半解,感到迷茫的话可以好好研究样例。
一个无向图,给死路的起点打标记,死路定义为从起点经过这条边后,无法不掉头走回起点。一条死路如果被一条有标记的死路不掉头地到达,那么这个死路的标记便不必打,求最少的标记数量和标记位置。
首先,边双连通分量中的边一定不是死路,所以先缩点,考虑边双构成的树的树边即可。
我们发现,可以把问题转化为打 Tag 和删 Tag 两步,而这两个阶段是互不干扰的,也就是说我们可以先打 Tag,然后考虑如何删除多余的 Tag 即可。
说明这个结论,因为死路的定义是确定的,所以无论如何删除 Tag,一条路该是死路仍然是死路,所以打 Tag 删 Tag 互不影响。
因为删 Tag 需要的是有打 Tag 的边能不掉头经过这条边。能经过一条边也就是能经过这条边的起点,所以我们对于一个点讨论是否存在有这种边连入即可。
这个时候可能就会产生问题,就是删除 Tag 之后,原本连入某个点的有 Tag 的边的 Tag 被删除后,这条边的 Tag 就不能被删除了。但是,我们知道能否到达是可以传递的,所以如果有一条边的 Tag 被删除,它删除的 Tag 的正确性不会受到影响,所以我们对每次打 Tag,将终点记录一个 Deleted 标记,最后将有标记的所有点的出边的 Tag 都删掉即可。
但是有一种情况比较特殊,就是一条入边不能删除自己的回边的标记,这时因为走了入边再走回边就相当于是掉头了,但是如果有多个带 Tag 的入边,就无需考虑这个问题,因为多条入边的回边可以相互被删除。这些情况每个点记录一个唯一带 Tag 入边的地址,特判一下即可。
void Del(BCC* x) {
EdgeB* Sid(x->Fst);
while (Sid) { if (Sid != x->Dont) Sid->Deleted = 1; Sid = Sid->Nxt; }
}
值得注意的是:不能每次入边连进来就执行这个操作,必须离线处理,因为缩点之后是菊花图的数据可以卡到 O(n2),打标记,最后统一删除可以保证每个点只回遍历一次它的连边。
我们发现,一条路径只要能通向一个非节点的双连通分量,在这个双连通分量里绕一圈,就可以不掉头地从原地反向出来。这个结论是接下来打 Tag 的基础。
对于一个连通块,随便找一个点为根,然后将边分成两类,连向父亲和连向儿子。
对于连向儿子的边,如果儿子的子树中有非节点的边双,那么不用打 Tag。如果没有,则说明这走条边后没法不掉头回到起点,则给连向儿子的边打 Tag。
如下是代码:
void DFSFall(BCC* x) {
EdgeB* Sid(x->Fst);
x->SubTree = x->Turn;
while (Sid) {
if (Sid->To != x->Fa) {
DFSFall(Sid->To), x->SubTree |= Sid->To->SubTree;
if (!(Sid->To->SubTree)) {
Sid->Ava = 1;
if (Sid->To->Dont) Sid->To->Dont = EB + 0x3f3f3f3f;
else Sid->To->Dont = EB + ((Sid - EB) ^ 1);
Sid->To->Deleted = 1;
}
}
Sid = Sid->Nxt;
}
}
然后是儿子连父亲的边,这种边需要讨论不打 Tag 的情况。
第一种是经过父亲往上走,能走到至少一个非节点边双,对于每个父亲,这种情况可以 DFS 过程中统计。
第二种情况,注意第二种情况都是建立在前面所说的情况不存在的前提下的。这时父亲存在儿子,它的子树中至少一个非节点边双。
第二种情况还需要讨论子树存在非节点边双的儿子的数量,当父亲只有一个儿子子树中存在非节点边双,则除了这个儿子以外都可以不打 Tag,但是需要在父亲连向这个特定的儿子的边上打 Tag。当有大于一个儿子的子树中有非节点边双,则按第一种情况处理即可。
接下来是程序实现:
void DFSRise(BCC* x) {
BCC* Son(NULL);
EdgeB* Sid(x->Fst);
char More(0);
while (Sid) {
if ((Sid->To != x->Fa) && (Sid->To->SubTree)) More = (Son ? 1 : 0), Son = Sid->To;
Sid = Sid->Nxt;
}
Sid = x->Fst;
if (More || (x->Turn)) {
while (Sid) {
if (Sid->To != x->Fa) Sid->To->Turn = 1, DFSRise(Sid->To);
Sid = Sid->Nxt;
}
return;
}
if (!Son) {
while (Sid) {
if (Sid->To != x->Fa) {
DFSRise(Sid->To), EB[((Sid - EB) ^ 1)].Ava = 1, x->Deleted = 1;
if (x->Dont) x->Dont = EB + 0x3f3f3f3f; else x->Dont = Sid;
}
Sid = Sid->Nxt;
}
return;
}
while (Sid) {
if (Sid->To != x->Fa) {
if (Sid->To == Son) {
DFSRise(Sid->To), EB[((Sid - EB) ^ 1)].Ava = 1, x->Deleted = 1;
if (x->Dont) x->Dont = EB + 0x3f3f3f3f; else x->Dont = Sid;
}
else Sid->To->Turn = 1, DFSRise(Sid->To);
}
Sid = Sid->Nxt;
}
}
接下来的内容就是人尽皆知的 Tarjan 了,直接缩点即可。
接下来给出代码省略缺省源的其余部分:
unsigned m, n, M;
unsigned A, C, D, t;
unsigned Cnt(0), Top(0), CntRoot(0), CntPrt(0);
struct Node;
struct BCC;
struct Edge {
Node* To;
Edge* Nxt;
}E[1000005];
struct EdgeIO {
unsigned Frm, To;
const inline char operator <(const EdgeIO& x) const { return (this->Frm ^ x.Frm) ? (this->Frm < x.Frm) : (this->To < x.To); }
}IO[1000005];
struct EdgeB {
BCC* To;
EdgeB* Nxt;
EdgeIO UsedTo;
char Ava, Deleted;
}EB[1000005];
struct BCC {
BCC* Fa;
EdgeB* Fst, * Dont;
char Turn, SubTree, Deleted;
}B[500005], * Root[500005], * CntB(B);
struct Node {
Edge* Fst;
BCC* Bel;
unsigned DFSr, Low;
}N[500005], * Stack[500005];
void Link(Node* x) {
Edge* Sid(x->Fst);
while (Sid) {
if (Sid->To->Bel) {
if (Sid->To->Bel < x->Bel) {
EB[Cnt].UsedTo.Frm = x - N, EB[Cnt].UsedTo.To = Sid->To - N;
EB[Cnt].Nxt = x->Bel->Fst, x->Bel->Fst = EB + Cnt, EB[Cnt++].To = Sid->To->Bel;
EB[Cnt].UsedTo.Frm = Sid->To - N, EB[Cnt].UsedTo.To = x - N;
EB[Cnt].Nxt = Sid->To->Bel->Fst, Sid->To->Bel->Fst = EB + Cnt, EB[Cnt++].To = x->Bel;
Sid->To->Bel->Fa = x->Bel;
}
}
Sid = Sid->Nxt;
}
}
void Shrink(Node* x, Edge* No) {
x->Low = x->DFSr = ++Cnt, Stack[++Top] = x;
Edge* Sid(x->Fst);
while (Sid) {
if (Sid != No) {
if (!(Sid->To->DFSr)) Shrink(Sid->To, E + ((Sid - E) ^ 1)), x->Low = min(x->Low, Sid->To->Low);
else x->Low = min(x->Low, Sid->To->Low);
}
Sid = Sid->Nxt;
}
if (x->DFSr == x->Low) {
++CntB, CntB->Turn = (Stack[Top] != x);
do { Stack[Top]->Bel = CntB; } while (Stack[Top--] != x);
}
}
signed main() {
n = RD(), m = RD(), M = (m << 1);
for (unsigned i(0); i < m; ++i) IO[i].Frm = RD(), IO[i].To = RD();
sort(IO, IO + m);
for (unsigned i(0); i < M; i += 2) {
C = IO[i >> 1].Frm, D = IO[i >> 1].To;
E[i].Nxt = N[C].Fst, N[C].Fst = E + i, E[i].To = N + D;
E[i ^ 1].Nxt = N[D].Fst, N[D].Fst = E + (i ^ 1), E[i ^ 1].To = N + C;
}
for (unsigned i(1); i <= n; ++i) if (!(N[i].DFSr)) Shrink(N + i, NULL), Root[++CntRoot] = CntB;
Cnt = 0;
for (unsigned i(1); i <= n; ++i) Link(N + i);
for (unsigned i(1); i <= CntRoot; ++i) DFSFall(Root[i]), DFSRise(Root[i]);
for (BCC* i(B + 1); i <= CntB; ++i) if (i->Deleted) Del(i);
for (unsigned i(0); i < Cnt; ++i) if (EB[i].Ava && (!EB[i].Deleted)) IO[++CntPrt] = EB[i].UsedTo;
sort(IO + 1, IO + CntPrt + 1);
printf("%u\n", CntPrt);
for (unsigned i(1); i <= CntPrt; ++i) printf("%u %u\n", IO[i].Frm, IO[i].To);
system("pause");
return Wild_Donkey;
}
CF652E
给一个无向连通图, 边权为 0/1, 求 a 到 b 是否存在一条边权和非 0 的不经过重复边的路径.
一个边双连通分量中, 一定存在方案能经过任意一条边的路径连接任意两点, 所以只要这个边双连通分量存在 1 边, 则经过这个边双连通分量的路径一定可以经过 1.
边双连通缩点, 然后将双连通分量的或作为缩点后的点权, 然后统计两点所属的双连通分量的路径上的点权或边权的或和即可, 为 0 即无解, 为 1 则有解.
说实在的这个题远不配紫题, 但是因为我做了, 我是利益既得者, 所以我不建议修改难度.
unsigned a[10005], m, n, M;
unsigned Cnt(0), C, D, t;
unsigned Top(0), Ans(0), Tmp(0);
char Last(0), E1(0);
struct BCC {
BCC* Son, * Bro, * Fa;
char Vis;
}B[300005], *CntB(B), * Now, *TOP;
struct Node;
struct Edge {
Node* To;
Edge* Nxt;
char Type;
}E[600005];
struct Node {
Edge* Fst;
BCC* Bel;
unsigned DFSr, Low;
}N[300005], *Stack[300005];
void Link(Node* x) {
Edge* Sid(x->Fst);
while (Sid) {
if (Sid->To->Bel) {
if (Sid->To->Bel != x->Bel) Sid->To->Bel->Bro = x->Bel->Son, x->Bel->Son = Sid->To->Bel, Sid->To->Bel->Fa = x->Bel, Sid->To->Bel->Vis |= Sid->Type << 2;
else x->Bel->Vis |= Sid->Type;
}
Sid = Sid->Nxt;
}
}
void Tarjan(Node* x, Edge* No) {
x->Low = x->DFSr = ++Cnt;
Stack[++Top] = x;
Edge* Sid(x->Fst);
while (Sid) {
if(Sid != No) {
if(!Sid->To->DFSr) Tarjan(Sid->To, E + ((Sid - E) ^ 1));
x->Low = min(x->Low, Sid->To->Low);
}
Sid = Sid->Nxt;
}
if(x->Low == x->DFSr) {
++CntB;
do Stack[Top]->Bel = CntB, Link(Stack[Top]);
while(Stack[Top--] != x);
}
}
int main() {
n = RD(), m = RD(), M = m << 1;
for (unsigned i(0); i < M; i += 2) {
C = RD(), D = RD(), E[i ^ 1].Type = E[i].Type = RD();
E[i].To = N + D, E[i].Nxt = N[C].Fst, N[C].Fst = E + i;
E[i ^ 1].To = N + C, E[i ^ 1].Nxt = N[D].Fst, N[D].Fst = E + (i ^ 1);
}
Tarjan(N + 1, NULL), Last = ((Now = N[C = RD()].Bel)->Vis |= 2), D = RD();
while (Now) {
Now->Vis |= Last;
Last = Now->Vis;
Now = Now->Fa;
}
Now = N[D].Bel, Last = 0;
for(;;) {
if(Now) TOP = Now;
else break;
Last |= Now->Vis;
if(Now->Vis & 2) break;
Now = Now->Fa;
}
Now = N[C].Bel;
while (Now != TOP) {
E1 |= Now->Vis;
Now = Now->Fa;
}
Now = N[D].Bel;
while (Now != TOP) {
E1 |= Now->Vis;
Now = Now->Fa;
}
Last |= (E1 >> 2);
printf((Last & 1) ? "YES\n" : "NO\n");
return Wild_Donkey;
}
圆方树
对于点双连通分量的缩点, 因为我们知道一个点可能在多个点双连通分量中, 所以可能会无法正确缩点, 所以我们选择变缩点为加点, 每个点双连通对应一个方点, 这个方点连接了所有属于该分量的所有点, 而所有圆点方点和连接圆方点的边组成了一个树形结构, 圆方树.
点双连通
相对来说, 点双连通的构造略复杂, 算法和强连通分量十分类似, 但是无向图不会有横叉边, 所以只需要讨论回边和树边.
对于树边, 仍然是 FromLow=min(ToLow,FromLow), 对于回边也是 FromLow=min(ToDfn,FromLow).
但是弹栈方式略有不同, 因为一个点是一个儿子所在双连通分量的根, 当且仅当 LowSon=Dfnx. 所以这时将所有 Son 的子树中的栈中的点弹出, 然后向新建的方点连边, 最后 x 向该方点连边, 然后递归其他的点即可.
CF487E
给一个无向连通图, 支持:
-
修改一个点的点权
-
询问两点之间所有简单路径上点权的最小值
对于一个割点, 经过它之后, 它不能再次经过, 相当于将这个点删掉, 一个连通块变成多个. 这时我们必须保证我们走过割点后, 位于我们目的地所在的连通块. 这就规定了从割点往外走的方向.
一条路径经过的所有的割点都是一定的, 但是割点之间每个点双中的任何点都是可以选择性经过的, 所以我们可以记录每个点双的最小点值, 然后查询必须经过的割点和割点之间的点双. 可以使用圆方树实现.
查询时, 求出两个点在圆方树上的路径, 然后将路径上的点的最小值进行统计即可, 用树链剖分实现.
但是因为支持修改, 我们不能每次修改一个割点就把包含它的所有点双的最小值修改一遍, 这样会被菊花图卡到 O(nq), 所以选择将每个割点的信息存到它圆方树上父亲中, 这样每次查询时, 如果需要查询它某个儿子的信息, 需要另外访问它本身.
但是大部分时候, 一个割点的儿子不是查询 LCA, 这时, 这个割点一定会被路径所包含. 所以我们只考虑割点的儿子是 LCA 的情况即可, 因为割点儿子一定是方点, 所以当方点作为 LCA, 统计方点父亲的信息即可.
unsigned a[200005];
unsigned m, n, q, M;
unsigned A, B, C, D, t;
unsigned Cnt(0), Top(0), Ans(0), Tmp(0);
char Op[5];
struct Seg {
Seg* LS, * RS;
unsigned Val;
}S[400005], * CntS(S);
struct Node;
struct Edge {
Edge* Nxt;
Node* To;
}E[200005];
struct Node {
Edge* Fst;
Seg* Root;
Node* Son, * Fa, * Bro, * Heavy, * Top;
unsigned DFSr, Low, Local, Size, Dep;
char Square;
multiset <unsigned> Val;
}N[200005], * Stack[100005], * CntN;
void Build(Seg* x, unsigned L, unsigned R) {
if (L == R) { x->Val = a[L];return; }
unsigned Mid((L + R) >> 1);
Build(x->LS = ++CntS, L, Mid), Build(x->RS = ++CntS, Mid + 1, R);
x->Val = min(x->LS->Val, x->RS->Val);
}
void Change(Seg* x, unsigned L, unsigned R) {
if (L == R) { x->Val = a[L]; return; }
unsigned Mid((L + R) >> 1);
if (A <= Mid) Change(x->LS, L, Mid);
else Change(x->RS, Mid + 1, R);
x->Val = min(x->LS->Val, x->RS->Val);
}
void Query(Seg* x, unsigned L, unsigned R) {
if ((A <= L) && (R <= B)) { Tmp = min(Tmp, x->Val);return; }
unsigned Mid((L + R) >> 1);
if (A <= Mid) Query(x->LS, L, Mid);
if (B > Mid) Query(x->RS, Mid + 1, R);
}
void Link(Node* x, Node* y, Edge* z) { z->Nxt = x->Fst, x->Fst = z, z->To = y; }
void Tarjan(Node* x, Edge* No) {
x->Low = (Stack[++Top] = x)->DFSr = ++Cnt;
Edge* Sid(x->Fst);
while (Sid) {
if (!(Sid->To->DFSr)) {
Tarjan(Sid->To, E + ((Sid - E) ^ 1)), x->Low = min(x->Low, Sid->To->Low);
if (x->DFSr == Sid->To->Low) {
Node* Cur(++CntN);
Cur->Bro = x->Son, x->Son = Cur, Cur->Square = 1, Cur->Fa = x;
do Stack[Top]->Bro = Cur->Son, Cur->Son = Stack[Top], Stack[Top]->Fa = Cur; while (Stack[Top--] != Sid->To);
}
}
x->Low = min(x->Low, Sid->To->DFSr);
Sid = Sid->Nxt;
}
}
void PreDFS(Node* x) {
if (!(x->Son)) return;
Node* Now(x->Son);
unsigned Mx(0);
x->Size = 1;
while (Now) {
Now->Dep = x->Dep + 1, PreDFS(Now), x->Size += Now->Size;
if (Now->Size > Mx) Mx = Now->Size, x->Heavy = Now;
Now = Now->Bro;
}
if (x->Square) {
Now = x->Son;
while (Now) {
x->Val.insert(Now->Local), Now = Now->Bro;
}
}
}
void DFS(Node* x) {
if (!(x->Son)) return;
x->DFSr = ++Cnt;
if (x->Square)a[Cnt] = *(x->Val.begin());
else a[Cnt] = x->Local;
if (!(x->Heavy)) return;
x->Heavy->Top = x->Top, DFS(x->Heavy);
Node* Now(x->Son);
while (Now) {
if (Now != x->Heavy) {
Now->Top = Now, DFS(Now);
}
Now = Now->Bro;
}
}
signed main() {
n = RD(), m = RD(), q = RD(), M = m << 1;
for (unsigned i(1); i <= n; ++i) N[i].Local = RD();
for (unsigned i(0); i < M; i += 2)
C = RD(), D = RD(), Link(N + C, N + D, E + i), Link(N + D, N + C, E + (i ^ 1));
CntN = N + n, Tarjan(N + 1, NULL);
Cnt = 0, N[1].Dep = 1, PreDFS(N + 1), N[1].Top = N + 1, DFS(N + 1), Build(S, 1, Cnt);
for (unsigned i(1); i <= q; ++i) {
scanf("%s", &Op), C = RD(), D = RD();
if (*Op == 'A') {
Node* QL(N + C), * QR(N + D);
if (QL == QR) { printf("%u\n", QL->Local); continue; }
Tmp = min(QL->Local, QR->Local);
if (QL->Fa && (!QL->Son)) QL = QL->Fa; if (QR->Fa && (!QR->Son)) QR = QR->Fa;
while (QL->Top != QR->Top) {
if (QL->Top->Dep < QR->Top->Dep) A = QR->Top->DFSr, B = QR->DFSr, QR = QR->Top->Fa;
else A = QL->Top->DFSr, B = QL->DFSr, QL = QL->Top->Fa;
Query(S, 1, Cnt);
}
if (QL->Dep < QR->Dep) A = QL->DFSr, B = QR->DFSr, Query(S, 1, Cnt), QR = QL;
else A = QR->DFSr, B = QL->DFSr, Query(S, 1, Cnt), QL = QR;
if (QL->Square) Tmp = min(Tmp, QL->Fa->Local);
printf("%u\n", Tmp);
}
else {
Node* Chan(N + C);
Chan->Fa->Val.erase(Chan->Local), Chan->Fa->Val.insert(Chan->Local = D);
a[A = Chan->Fa->DFSr] = *(Chan->Fa->Val.begin()), Change(S, 1, Cnt);
}
Chan->Local = D;
if (Chan->Son) a[A = Chan->DFSr] = Chan->Local, Change(S, 1, Cnt);
}
}
return Wild_Donkey;
}
POJ2942
有 n 个骑士经常举行圆桌会议, 商讨大事. 每次圆桌会议至少有 3 个骑士参加, 且相互憎恨的骑士不能坐在圆桌的相邻位置. 如果发生意见分歧, 则需要举手表决, 因此参加会议的骑士数目必须是大于 1 的奇数, 以防止赞同和反对票一样多. 知道那些骑士相互憎恨之后, 你的任务是统计有多少骑士不可能参加任何一个会议.
给出的边是不能相邻的人, 那么我们给这些骑士建完全图, 然后将这个完全图删掉给出的边, 得到原图的补图, 这时, 一个合法的会议就是补图上的一个简单奇环.
既然是找不能参加会议的人, 那么我们只要找不被任何奇环包含的点即可.
奇环一定是被包含在点双里面的, 所以我们不考虑不同点双之间的点的影响. 对于一个点双, 如果存在一个奇环, 那么这个点双内所有点都能被至少一个奇环所包含.
证明也很简单, 因为点双里没有割点, 所以已知存在的奇环和其它任意一点之间都会又有至少两个点连接.
假设取奇环和其它点连接的两个点 u, v, 这两个点因为在奇环上, 所以它们之间既存在奇数长度的路径, 也存在偶数长度的路径. 因为点双内, 对于两个点, 任选一个第三点都能找到一条简单路径经过第三点连接两点. 所以对于任意点双内的点 x, 它如果不在已知的奇环内, 一定存在一条简单路径经过 x 连接 u, v, 无论路径奇偶, 都能找到另一条已知奇环上的路径, 和经过 x 的路径首尾连接, 形成奇环.
既然有了这个结论, 一个点双内只要找到一个奇环, 那么它的所有节点都会被至少一个奇环包含. 接下来对每个点双找奇环即可.
找奇环可以通过 BFS, 每个点双找一个原点, 然后记录原点到别的点是否有奇数或偶数的路径, 当找到一个点, 它到原点既有奇数路径也有偶数路径时, 则找到奇环.
查询一个点是否在有奇环的点双里, 可以建立圆方树, 在每次找奇环后, 将点双是否有奇环的信息存到对应点方点上, 如果一个方点有奇环, 则它的父亲被包含在这个方点的点双里, 则给父亲打上标记. 对于一个圆点, 如果它的父亲有奇环, 则这个圆点也应该打上标记. 这样就统计了所有圆点的父亲和儿子有奇环的情况.
最后统计没有标记的圆点数即可.
unsigned m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
unsigned Top(0), Tl(0), Hd(0);
char b[1005][1005];
struct Node;
struct Edge {
Node* To;
Edge* Nxt;
}E[2000005], * CntE(E);
struct Node {
Edge* Fst;
Node* Fa;
unsigned DFSr, Low;
char Situ;
}N[1005], * Q[1005], * Stack[1005], * CntN(N);
void Clr() {
memset(N, 0, (CntN - N + 1) * (sizeof(Node)));
n = RD(), m = RD(), CntE = E, CntN = N + n;
Cnt = Ans = 0;
}
void Tarjan(Node* x) {
Edge* Sid(x->Fst);
x->Low = (Stack[++Top] = x)->DFSr = ++Cnt;
while (Sid) {
if (Sid->To->DFSr) x->Low = min(x->Low, Sid->To->DFSr);
else {
Tarjan(Sid->To), x->Low = min(x->Low, Sid->To->Low);
if (Sid->To->Low == x->DFSr) {
Node* Cur(++CntN); Cur->Fa = x;
do Stack[Top]->Fa = Cur;
while (Stack[Top--] != Sid->To);
}
}
Sid = Sid->Nxt;
}
}
void BFS(Node* x) {
Hd = Tl = 0, Q[++Tl] = x->Fa, x->Fa->Situ = 1;
while (Hd ^ Tl) {
Node* Cur(Q[++Hd]);
Edge* Sid(Cur->Fst);
if (!(Cur->Situ ^ 3)) {
while (Sid) {
if ((Sid->To->Fa == x) || (x->Fa == Sid->To)) {
if (!(Sid->To->Situ)) Q[++Tl] = Sid->To;
Sid->To->Situ = 3;
}
Sid = Sid->Nxt;
}
}
else while (Sid) {
if ((Sid->To->Fa == x) || (x->Fa == Sid->To)) {
if (!(Sid->To->Situ)) Q[++Tl] = Sid->To;
Sid->To->Situ |= (Cur->Situ ^ 3);
if (!(Sid->To->Situ ^ 3)) { x->Situ = 3; return; }
}
Sid = Sid->Nxt;
}
}
}
signed main() {
for (;;) {
Clr();
if (!n) return Wild_Donkey;
for (unsigned i(1); i <= m; ++i) A = RD(), B = RD(), b[A][B] = b[B][A] = 1;
for (unsigned i(1); i <= n; ++i) {
b[i][i] = 1;
for (unsigned j(1); j <= n; ++j)
if (!b[i][j]) (++CntE)->Nxt = N[i].Fst, N[i].Fst = CntE, CntE->To = N + j; else b[i][j] = 0;
}
for (unsigned i(1); i <= n; ++i) if (!(N[i].DFSr)) Tarjan(N + i);
for (Node* i(CntN); i > N + n; --i) BFS(i);
for (Node* i(N + n + 1); i <= CntN; ++i) if (!((i->Situ) ^ 3)) i->Fa->Situ = 3;
for (unsigned i(1); i <= n; ++i) if (N[i].Fa && (N[i].Fa->Situ == 3)) N[i].Situ = 3;
for (unsigned i(1); i <= n; ++i) Ans += (N[i].Situ ^ 3) ? 1 : 0;
printf("%u\n", Ans);
}
}
UVA1108
在无向连通图上涂黑一些点, 使得任何一个点删除后, 每个连通块仍有至少一个黑点.
求最少涂黑的点数和保证涂黑点最少前提下的方案数.
感性理解, 不涂割点, 因为如果涂割点, 那么把它删掉之后, 每个连通块都需要一个黑点, 加起来最少是连通块个数 +1 个点要涂黑. 而如果不涂割点, 那么删除这个割点之后, 最少需要连通块个数个点要涂黑.
对于一个点双图, 一个点被删掉后, 剩下的点仍然连通, 所以只需要涂黑 2 个点即可, 方案数就是 (n2)=n∗(n−1)2.
而对于连通图的点双分量, 讨论它的割点数量, 如果没有割点, 说明这是一个点双图, 按上面的规则统计即可.
如果有 1 个割点, 则删除这个割点后, 该点双剩余的点形成一个连通块, 则该点双内部需要至少一个黑点, 且该黑点不能是割点, 而外部也需要至少一个黑点. 因此方案数是该点双非割点点数.
如果删除除割点以外的点, 则该分量仍和外界连通, 而外界的点至少有一个黑点, 所以仍合法.
对于两个及以上割点的点双, 我们可以完全相信与它相连的其它连通块各自都有黑点, 而只删一个割点是不能切断该点双和别的连通块的一切连接的, 所以这种点双无需涂黑任何点.
所以我们只要 Tarjan 求出所有的点双的非割点点数和割点点数, 然后将所有包含 1 个割点的点双的非割点数乘积即可. 还要特判点双图的情况.
有一个值得注意的问题: Tarjan 一般会默认第一个点是割点, 需要扫描和它有边相连的每个点所属的编号最大的点双是否是同一个, 如果是同一个, 说明不是割点, 需要修正它所在点双的数据.
unsigned long long Ans(1);
unsigned m, n, A, B, C, D, t;
unsigned Size[100005], CntCut[100005];
unsigned Cnt(0), Tmp(0), Top(0), BCC(0);
struct Node;
struct Edge {
Node* To;
Edge* Nxt;
}E[100005], * CntE(E);
struct Node {
Edge* Fst;
unsigned DFSr, Low, Bel;
char Cut;
}N[100005], * Stack[100005];
inline void Clr() {
memset(Size, 0, (BCC + 1) << 2);
memset(CntCut, 0, (BCC + 1) << 2);
memset(N, 0, (n + 1) * sizeof(Node));
m = RD(), BCC = Cnt = n = 0, Ans = 1, CntE = E;
}
void Tarjan(Node* x) {
Edge* Sid(x->Fst);
(Stack[++Top] = x)->Low = x->DFSr = ++Cnt;
while (Sid) {
if (Sid->To->DFSr) x->Low = min(x->Low, Sid->To->DFSr);
else {
Tarjan(Sid->To), x->Low = min(x->Low, Sid->To->Low);
if (Sid->To->Low == x->DFSr) {
Size[++BCC] = x->Cut = 1, CntCut[BCC] = 1;
do ++Size[BCC], CntCut[BCC] += Stack[Top]->Cut, Stack[Top]->Bel = BCC;
while (Stack[Top--] != Sid->To);
}
}
Sid = Sid->Nxt;
}
}
signed main() {
for (unsigned T(1);;++T) {
Clr();
if (!m) { return Wild_Donkey; }
for (unsigned i(1); i <= m; ++i) {
n = max(n, C = RD()), n = max(n, D = RD());
(++CntE)->Nxt = N[C].Fst, N[C].Fst = CntE, CntE->To = N + D;
(++CntE)->Nxt = N[D].Fst, N[D].Fst = CntE, CntE->To = N + C;
}
Tarjan(N + 1), Cnt = 0, N[1].Bel = N[1].Fst->To->Bel;
for (Edge* i(N[1].Fst); i; i = i->Nxt, ++Tmp)
if (N[1].Bel != i->To->Bel) N[1].Bel = 0;
if (N[1].Bel) --CntCut[BCC];
if (BCC == 1) Cnt = 2, Ans = (n * (n - 1)) >> 1;
else for (unsigned i(1); i <= BCC; ++i) if (CntCut[i] == 1) Ans *= Size[i] - 1, Cnt += 1;
printf("Case %u: %u %llu\n", T, Cnt, Ans);
}
}
三倍经验? (UVA1108+HNOI2012+SP16185)
CF97E
给一个简单无向图, 询问两个点之间是否存在长度为奇数的简单路径. (简单路径定义为没有重复点的路径, 路径长度定义为边数)
这里简单路径的定义是每个点出现最多一次的路径, 所以优先考虑点双. 发现点双里面, 只要有至少一个奇环, 任意两点间都存在奇路径.
继续探索发现如果每个点双对应的方点的父亲称为 "主割点", 那么一个点双内, 除了主割点, 一个点到主割点有三种状态, 没有奇路径, 存在奇偶路径, 仅有奇路径. 分别称三种类型的节点为偶点, 奇偶点, 奇点.
发现有奇环的点双里, 任意两点间都既有奇路径, 也有偶路径, 所以除主割点外的点都是奇偶点.
如果没有奇环, 则 BFS 找到每个点到主点的最短路, 最短路的奇偶性就是这个点的奇偶性.
对于找奇环和最短路, 为了保证不会被菊花图卡到 O(n2), 借助 Calvincheng1231 的题解中的方法, 每个点双连通分量建一个新的点双连通图.
对于点双内的情况, 两个非主割点的点之间有简单奇路径, 当且仅当有至少一个点是奇偶点, 或有一个点是奇点.
因为这种情况可以取两个点到主割点的路径, 使得路径总和为奇数, 把重合部分删除, 因为删除一条边, 相当于它两次经过的贡献都删除了, 所以奇偶性不变.
对于点双内, 除主割点外的一点到主割点的路径, 这个点只要是奇偶点或奇点, 就能找到一条简单奇路径.
接下来讨论一般情况, 也就是点双间的路径, 因为两点间路径上的割点已经确定了, 所以我们只需要依次讨论端点和割点间路径的情况即可. 这些点将路径分成了几段.
因为这几段分别在不同的点双内, 所以每一段的情况就可以当作点双内部的情况来讨论, 对于既有奇数又有偶数路径的段, 我们称其为奇偶段, 对于只有奇数路径的段, 称奇段, 没有奇数路径的段, 称偶段.
类似地, 整条路经存在奇路径, 当且仅当这些段中有奇偶段, 或者这些段中的奇段数量为奇数.
对于一段路径, 如果它的两端有一端是路径所在点双的主割点, 那么另一个端点的类型就是这一段的类型.
如果两端都不是路径所在点双的主割点, 那么这一段分成两端, 两段类型分别是两个点的类型.
所以我们需要做的就是查询圆方树上两点间路径上不同类型的圆点数量 (除去 LCA). 就能得到这些段的类型数量, 然后 O(1) 判断即可.
用树链剖分维护圆方树, 支持查询路径三种类型的点的数量 (其实偶点数量和答案无关, 无需维护). 由于无需修改, 所以只需要用前缀和查询区间和即可.
总复杂度 O(n+m+qlogn).
unsigned m, M, n, q, Bd;
unsigned A, B, C, D, t;
unsigned STop(0), ETop(0), Hd, Tl;
unsigned Cnt(0), CntCo(0), Ans[3];
unsigned Sum[200005][2], Tmp(0);
struct Node;
struct NNode;
struct Edge {
Node* To, * Frm;
Edge* Nxt;
}E[200005], *EStack[200005];
struct Node {
Edge* Fst;
NNode* Last;
Node* Fa, * Bro, * Son, * Heavy, * Top;
unsigned DFSr, Low, Dep, Size, BelC;
char Type;
}N[200005], * Stack[100005], * CntN;
struct NEdge {
NNode* To;
NEdge* Nxt;
}NE[400005], *CntNE(NE);
struct NNode{
NEdge* Fst;
Node* Old;
char Col, Dist;
}NN[200005], * Q[200005], *CntNN(NN);
inline void Tarjan(Node* x) {
x->Low = x->DFSr = ++Cnt, x->BelC = CntCo, Stack[++STop] = x;
Edge* Sid(x->Fst);
while (Sid) {
EStack[++ETop] = Sid;
if(Sid->To->DFSr) {
if(Sid->To->Fa) --ETop;
x->Low = min(x->Low, Sid->To->DFSr);
}
else {
unsigned LastTop(ETop);
Tarjan(Sid->To), x->Low = min(x->Low, Sid->To->Low);
if(Sid->To->Low == x->DFSr) {
Node* Cur(++CntN);
Cur->Fa = x, Cur->Bro = x->Son, x->Son = Cur;
x->Last = Cur->Last = ++CntNN, CntNN->Old = x;
do {
Stack[STop]->Bro = Cur->Son, Cur->Son = Stack[STop];
Stack[STop]->Last = ++CntNN, (CntNN->Old = Stack[STop])->Fa = Cur;
} while (Stack[STop--] != Sid->To);
NNode * LiF, * LiT;
do {
LiF = EStack[ETop]->Frm->Last, LiT = EStack[ETop]->To->Last;
(++CntNE)->Nxt = LiF->Fst, LiF->Fst = CntNE, CntNE->To = LiT;
(++CntNE)->Nxt = LiT->Fst, LiT->Fst = CntNE, CntNE->To = LiF;
} while ((ETop--) ^ LastTop);
}
}
Sid = Sid->Nxt;
}
}
inline void BFS(Node* x) {
char Flg(0);
Hd = Tl = 0, (Q[++Tl] = x->Last)->Col = 1, x->Last->Dist = 1;
while (Hd ^ Tl) {
NNode* Cur(Q[++Hd]);
NEdge* Sid(Cur->Fst);
while (Sid) {
Sid->To->Col |= (Cur->Col ^ 3);
if(Sid->To->Col == 3) {Flg = 1; break;}
if(!(Sid->To->Dist)) (Q[++Tl] = Sid->To)->Dist = Cur->Dist + 1;
Sid = Sid->Nxt;
}
if(Flg) break;
}
if(Flg) x->Type = 2;
else
for (unsigned i(2); i <= Hd; ++i)
Q[i]->Old->Type = ((Q[i]->Dist & 1) ? 0 : 1);
}
inline void PreDFS (Node* x) {
x->Size = 1;
Node* Cur(x->Son);
unsigned Mx(0);
while (Cur) {
Cur->Dep = x->Dep + 1, PreDFS(Cur), x->Size += Cur->Size;
if(Cur->Size > Mx) x->Heavy = Cur, Mx = Cur->Size;
Cur = Cur->Bro;
}
}
inline void DFS (Node* x) {
x->DFSr = ++Cnt;
if(x->Type) Sum[Cnt][x->Type - 1] = 1;
if(!(x->Heavy)) return;
x->Heavy->Top = x->Top, DFS(x->Heavy);
Node* Cur(x->Son);
while (Cur) {
if(Cur != x->Heavy) Cur->Top = Cur, DFS(Cur);
Cur = Cur->Bro;
}
}
inline char Ask(Node* x, Node* y) {
Ans[1] = Ans[2] = 0;
while (x->Top != y->Top) {
if(x->Top->Dep < y->Top->Dep) swap(x, y);
C = x->Top->DFSr, D = x->DFSr, x = x->Top->Fa;
Ans[1] += Sum[D][0] - Sum[C - 1][0];
Ans[2] += Sum[D][1] - Sum[C - 1][1];
}
if(x->Dep < y->Dep) swap(x, y);
C = y->DFSr, D = x->DFSr, x = y;
Ans[1] += Sum[D][0] - Sum[C - 1][0];
Ans[2] += Sum[D][1] - Sum[C - 1][1];
--Ans[x->Type];
if(Ans[2] || (Ans[1] & 1)) return 1;
return 0;
}
signed main() {
n = RD(), M = ((m = RD()) << 1), CntN = N + n;
for (unsigned i(0); i < M; i += 2) {
A = RD(), B = RD();
E[i].Nxt = N[A].Fst, N[A].Fst = E + i;
E[i ^ 1].Nxt = N[B].Fst, N[B].Fst = E + (i ^ 1);
E[i].To = N + B, E[i].Frm = N + A;
E[i ^ 1].To = N + A, E[i ^ 1].Frm = N + B;
}
for (unsigned i(1); i <= n; ++i) if(!(N[i].DFSr)) ++CntCo, Tarjan(N + i);
Cnt = 0;
for (Node* i(N + n + 1); i <= CntN; ++i) BFS(i);
for (unsigned i(1); i <= n; ++i) if(N[i].Fa && N[i].Fa->Type) N[i].Type = 2;
for (unsigned i(1); i <= n; ++i) if(!N[i].Size) N[i].Dep = 1, PreDFS(N + i);
for (unsigned i(1); i <= n; ++i) if(!N[i].Top) N[i].Top = N + i, DFS(N + i);
for (unsigned i(1); i <= Cnt; ++i) Sum[i][0] += Sum[i - 1][0], Sum[i][1] += Sum[i - 1][1];
for (unsigned i(RD()); i; --i) {
A = RD(), B = RD(), --q;
if(A == B) {printf("No\n");continue;}
if(N[A].BelC ^ N[B].BelC) {printf("No\n");continue;}
printf(Ask(N + A, N + B) ? "Yes\n" : "No\n");
}
return Wild_Donkey;
}
CF962F
给一个简单无向图, 求哪些边恰好在一个简单环内.
根据本题对简单环的定义, 可以知道是考虑点双.
对于一个存在多个简单环的点双, 每条边都不在答案中, 对于没有简单环的点双, 每条边也不在答案中.
所以答案就是所有只有一个简单环的点双的边.
一个简单环作为点双, 需要这个点双内部的点的度数都是 2 (连向该点双的点的度数).
标记每个圆点在它父亲代表的点双内的度, 对于方点, 记录它的父亲在它对应的点双内的度. 对于每个方点, 如果它和它的儿子的度都是 2, 这时标记这个方点为可行.
求答案时, 将所有标记为可行的方点的点双内的边全部标记为输出, 然后扫描所有边, 统计输出边数, 然后输出对应编号即可.
unsigned m, n, M, Top(0);
unsigned A, B, C, D, t;
unsigned Cnt(0), Tmp(0);
char Calced[100005], Ans[100005];
struct Node;
struct Edge {
Node* To;
Edge* Nxt;
}E[200005];
struct Node {
Edge* Fst;
Node* Son, * Bro, * Fa;
unsigned DFSr, Low, Deg;
char NoAva;
}N[200005], * Stack[100005], * CntN;
inline void Tarjan(Node* x) {
x->Low = x->DFSr = ++Cnt, Stack[++Top] = x;
Edge* Sid(x->Fst);
while (Sid) {
if(Sid->To->DFSr) x->Low = min(x->Low, Sid->To->DFSr);
else {
Tarjan(Sid->To), x->Low = min(x->Low, Sid->To->Low);
if(Sid->To->Low == x->DFSr) {
Node* Cur(++CntN);
Cur->Bro = x->Son, x->Son = Cur, Cur->Fa = x;
do Stack[Top]->Bro = Cur->Son, Cur->Son = Stack[Top], Stack[Top]->Fa = Cur;
while (Stack[Top--] != Sid->To);
}
}
Sid = Sid->Nxt;
}
return;
}
inline void PreDFS (Node* x) {
Node* Cur(x->Son);
while(Cur) PreDFS(Cur), Cur = Cur->Bro;
Edge* Sid(x->Fst);
Node* GrFa(x->Fa);
if(GrFa) GrFa = GrFa->Fa;
while(Sid) {
if(!(Calced[(Sid - E) >> 1])) {
Calced[(Sid - E) >> 1] = 1;
if(Sid->To->Fa == x->Fa) ++(x->Deg), ++(Sid->To->Deg);
if(Sid->To == GrFa) ++(x->Deg), ++(x->Fa->Deg);
}
Sid = Sid->Nxt;
}
}
inline void DFS (Node* x) {
Node* Cur(x->Son);
if(x - N > n) {
if(x->Deg ^ 2) x->NoAva = 1;
while(Cur) {
DFS(Cur);
if(Cur->Deg ^ 2) x->NoAva = 1;
Cur = Cur->Bro;
}
} else while(Cur) DFS(Cur), Cur = Cur->Bro;
}
inline void PlsDFS (Node* x) {
Node* Cur(x->Son);
while(Cur) PlsDFS(Cur), Cur = Cur->Bro;
Edge* Sid(x->Fst);
Node* GrFa(x->Fa);
if(GrFa) GrFa = GrFa->Fa;
while(Sid) {
if(Calced[(Sid - E) >> 1]) {
Calced[(Sid - E) >> 1] = 0;
if((Sid->To->Fa == x->Fa) && (!(x->Fa->NoAva))) Ans[(Sid - E) >> 1] = 1;
if((Sid->To == GrFa) && (!(x->Fa->NoAva))) Ans[(Sid - E) >> 1] = 1;
}
Sid = Sid->Nxt;
}
}
signed main() {
CntN = N + (n = RD()), M = ((m = RD()) << 1);
for (unsigned i(0); i < M; i += 2) {
A = RD(), B = RD();
E[i].Nxt = N[A].Fst, N[A].Fst = E + i;
E[i ^ 1].Nxt = N[B].Fst, N[B].Fst = E + (i ^ 1);
E[i].To = N + B, E[i ^ 1].To = N + A;
}
for (unsigned i(1); i <= n; ++i) if(!N[i].DFSr)
Tarjan(N + i), PreDFS(N + i), DFS(N + i), PlsDFS(N + i);
Cnt = 0;
for (unsigned i(0); i < m; ++i) Cnt += Ans[i];
printf("%u\n", Cnt);
for (unsigned i(0); i < m; ++i) if(Ans[i]) printf("%u ", i + 1);
return Wild_Donkey;
}
Day16: 图论
拓扑排序
仅有向无环图, 过水已隐藏
CF1385E
给一个混合图, 既有有向边也有无向边, 定向无向边使得它是一个 DAG.
只看有向边拓扑排序, 无向边连向拓扑序大的点.
unsigned m, n, q, Hd, Tl;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
unsigned Qry[200005][2];
unsigned Top;
struct Node;
struct Edge{
Node* To;
Edge* Nxt;
}E[200005], *CntE(E);
struct Node {
Edge* Fst;
unsigned ToPo, Deg;
}N[200005], * Q[200005];
inline void Clr() {
for (unsigned i(1); i <= n; ++i) N[i].Fst = NULL, N[i].Deg = NULL;
n = RD(), m = RD(), Hd = Tl = q = 0;
}
signed main() {
t = RD();
for (unsigned T(1); T <= t; ++T){
Clr();
for (unsigned i(1); i <= m; ++i) {
C = RD(), A = RD(), B = RD();
if(C) (++CntE)->Nxt = N[A].Fst, N[A].Fst = CntE, CntE->To = N + B, ++N[B].Deg;
else Qry[++q][0] = A, Qry[q][1] = B;
}
for (unsigned i(1); i <= n; ++i) if(!N[i].Deg) Q[++Tl] = N + i;
while (Tl ^ Hd) {
Node* Cur(Q[++Hd]);
Edge* Sid(Cur->Fst);
Cur->ToPo = ++Cnt;
while(Sid) {
if(!(--(Sid->To->Deg))) Q[++Tl] = Sid->To;
Sid = Sid->Nxt;
}
}
if(Tl < n) {printf("NO\n"); continue;}
printf("YES\n");
for (unsigned i(1); i <= q; ++i) {
if(N[Qry[i][0]].ToPo > N[Qry[i][1]].ToPo) swap(Qry[i][0], Qry[i][1]);
printf("%u %u\n", Qry[i][0], Qry[i][1]);
}
for (unsigned i(1); i <= n; ++i) {
Edge* Sid(N[i].Fst);
while (Sid) {
printf("%u %u\n", i, Sid->To - N);
Sid = Sid->Nxt;
}
}
}
return Wild_Donkey;
}
基环树
外向树无法拓扑排序, 内向树拓扑排序后剩余一个环.
DAG 最长链
给一个点带权 DAG, 问选一条链最大权值是多少.
拓扑排序后 DP.
设计状态 fx 是从 x 出发的最大链权, 转移是用从 x 有一条出边能到达的点 y 更新 x, 使得 fx=ax+max(fy), 转移顺序需要拓扑序从大到小, 否则会有冲突.
传递闭包
给一个 DAG, 求每个点能到达哪些点.
仍然拓扑排序 + DP, 然后从大到小转移.
边界条件是汇点只能到达自己.
设计状态值 f 是 ⌊n64⌋ 个 64 位整数.
转移是对于任意 x 有出边到达的 y, fx=fx∪fy.
P7480
数轴上有 n 个加油站, 每个加油站 i 对应位置 xi 和油价 ci.
一开始没油, 起点有加油站, 油箱容量无限, 一单位油走一单位路, 给一个起点和终点, 求最小花费.
策略是每次到一个油钱更小的加油站, 有单调栈求出每个加油站左右第一个更便宜的加油站, 连边, 边权是 当前油价×距离.
因为一定是向更便宜的点连边, 所以有向图无环, 是 DAG, 跑起点到所有点的最短路后分别更新答案.
unsigned m, n, Frm, Lst;
int T;
unsigned StkL[100005], StkR[100005], Top1(0), Top2(0);
unsigned List[100005];
unsigned Cnt(0), Ans(0), Tmp(0);
struct Node;
struct Sta {
unsigned Val, Pos;
const unsigned char operator < (const Sta &x) { return Pos < x.Pos; }
}S[100005], FindT;
struct Edge {
Node* To;
Edge* Nxt;
unsigned long long Val;
}E[100005], * CntE(E);
struct Node {
Edge* Fst;
unsigned long long Dis;
}N[100005];
inline void Link(const unsigned &x, const unsigned &y, const unsigned long long &z) {
(++CntE)->Nxt = N[x].Fst, N[x].Fst = CntE, CntE->To = N + y, CntE->Val = z;
}
signed main() {
n = RD() + 1, FindT.Pos = RDsg() + 1000000000, S[n].Pos = RDsg() + 1000000000;
for (unsigned i(1); i < n; ++i) S[i].Val = RD(), S[i].Pos = 1000000000 + RDsg();
sort(S + 1, S + n + 1), Frm = lower_bound(S + 1, S + n + 1, FindT) - S;
for (unsigned i(Frm), j(Frm), k(S[Frm].Val);;) {
while(i && (S[i].Val >= k)) --i;
while((j <= n) && (S[j].Val >= k)) ++j;
if(S[i].Val > S[j].Val) k = S[i].Val, StkL[++Top1] = i;
else k = S[j].Val, StkR[++Top2] = j;
if(!k) break;
}
if(S[StkR[Top2 - 1]].Pos == S[StkR[Top2]].Pos) StkR[Top2 - 1] = StkR[Top2], --Top2;
for (unsigned i(1), j(1), k(Frm); j <= Top2;) {
List[++Cnt] = k;
Link(k, StkL[i], (unsigned long long)S[k].Val * (S[k].Pos - S[StkL[i]].Pos));
Link(k, StkR[j], (unsigned long long)S[k].Val * (S[StkR[j]].Pos - S[k].Pos));
if(S[StkL[i]].Val > S[StkR[j]].Val) k = StkL[i++];
else k = StkR[j++];
}
for (unsigned i(1); i <= n; ++i) N[i].Dis = 0x3f3f3f3f3f3f3f3f;
N[Frm].Dis = 0;
for (unsigned i(1); i <= Cnt; ++i) {
Node* Cur(N + List[i]);
Edge* Sid(Cur->Fst);
while (Sid) {
Sid->To->Dis = min(Sid->To->Dis, Cur->Dis + Sid->Val);
Sid = Sid->Nxt;
}
}
printf("%llu\n", N[StkR[Top2]].Dis);
return Wild_Donkey;
}
最小拓扑序
因为一个 DAG 的拓扑序是不唯一的, 所以一定存在一个方案, 使得拓扑序排出的节点序列字典序最小.
只要在统计时将字典序小的先删除即可.
树上拓扑序计数
统计外向树的拓扑序不同的可能的情况总数.
如果一个点有多个子树, 则两两子树的节点在拓扑序中的先后顺序随意, 所以可以直接在 Sizex−1 个位置中任选 SizeSon 个分配给儿子即可, 方案数 (Sizex−1SizeSon).
对于第二个儿子, 在 Sizex−1−SizeSon1 种中选 SizeSon2 种即可.
所以总的分配方案数是
最后再用乘法原理统计每个儿子内部分配情况即可, 所以 x 子树的总方案数为:
拓扑序计数
给一个 n 点 m 边有向图, 每条边可能出现, 对 2m 种情况, 求每种情况拓扑序方案数之和.
n≤20
枚举拓扑序, 对于每个拓扑序, 累加可行的连边情况.
对节点状压, fi 表示包含集合 i 中的所有拓扑序, 符合条件的连边情况总和. 对于一个点集, 只考虑这些点之间的边.
那么 i 只包含一个点的时候, 是边界情况, fi=1, 对于转移来说, 枚举一个点加入点集, 放到集合最后.
Edgei,j 是所有 i 集合中的点连向点 j 的边数.
新♂题♂目
对长为 n 的未知正整数序列给 m 个约束条件表示 ax≤ay, 求 min(maxai).
每个约束条件连边 (x,y), 变成求 DAG 最长链的点数.
拓扑排序, 设计状态 fi 表示一个点为终点的最长链点数, 按顺序转移, 对于一个点 x, 它可以更新有出边到达的点 y, fy=max(fy,fx+1).
答案即为 max(fi).
NWRRC2015
对于 [1,n] 的排列, 给 m 个限制, 第 i 个限制描述 bi 出现在 ai, ci 之间. 保证存在一个排列满足所有限制.
构造一个 n 的排列至少满足 ⌈m2⌉ 个限制.
每个限制连接两条有向边 (ai,bi), (ci,bi), 因为所有限制都可以被满足, 所以在原序列中的端点一定入度为 0.
这个图虽然存在环, 但是我们对这个图进行拓扑排序, 一次删除一个约束的两条边, 仍然是可以将所有点入队出队的, 但是排序后仅能保证其中每个约束中, b 点不会同时排在 a, c 前面. 但是这已经足够做此题了.
证明很简单, 如果一个 b 的度变成 0, 一定是它的所有入边都被删除了, 所以不存在 b 被删除, a, c 都仍未删除的情况.
我们按拓扑序考虑将点加入最左边还是最右边, 从两边往中间堆元素, 直到填满排列为止.
对于一个约束, 第一个放入的如果是 b, 则无论 a, b 怎么放, 都不可能满足约束, 而我们的拓扑排序不存在 b 第一个放的情况.
如果第一个放的是 a 或 c, 第二个放的点的位置就决定了该约束是否能满足.
如果第二个放的是 b, 那么它放在第一个放的元素同侧, 则最后一个元素无论怎么放, 约束都满足. 如果放在异侧, 则无论最后一个元素怎么放, 约束都不满足.
如果第二个放的是 a 或 c 那么第三个放的一定是 b, 所以第一个和第二个放的 a, c 只要在异侧, 约束一定满足, 在同侧则一定不满足.
我们对于每个枚举的元素, 统计它属于的约束中, 有多少次是第二个放的元素, 然后统计这些情况中, 是放在左端满足的约束多还是放在右端满足的约束多, 放到满足约束多的一侧, 这样就保证了一定满足 ⌈m2⌉ 个限制.
因为每个约束会给 bi 带来两个入度, 而拓扑排序时我们需要给 bi 减去两个入度, 所以为了方便, 不如直接用一个入度表示一个约束.
过程中我们一遍拓扑排序一边处理, 因为每个点的位置只和已经放入排列中的点有关, 所以这样处理也是正确的.
unsigned m, n, M;
unsigned Top(0), Tl(0), Hd(0);
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans[100005], Tmp(0), BdL(0), BdR;
struct Que;
struct Node {
vector<Que*> Bel;
unsigned Deg;
char Vis, Le;
}N[100005], * Queue[100005];
struct Que {
Node* Le, * Ri, * Mid;
Que* Nxt;
}Q[100005];
signed main() {
BdR = (n = RD()) + 1, m = RD();
for (unsigned i(1); i <= m; ++i) {
A = RD(), B = RD(), C = RD(), ++N[B].Deg;
Q[i].Le = N + A, N[A].Bel.emplace_back(Q + i);
Q[i].Mid = N + B, N[B].Bel.emplace_back(Q + i);
Q[i].Ri = N + C, N[C].Bel.emplace_back(Q + i);
}
for (unsigned i(1); i <= n; ++i) if(!N[i].Deg) Queue[++Tl] = N + i;
while (Tl ^ Hd) {//Topo and Solve
Node* Cur(Queue[++Hd]);
unsigned PutLeft(100000);
Cur->Vis = 1;
for (auto Prs:Cur->Bel) {
if(Cur == Prs->Le) {//Cur is A
if(Prs->Ri->Vis) {//2nd or 3rd
if(!(Prs->Mid->Vis)) {if(Prs->Ri->Le) --PutLeft; else ++PutLeft;}//2nd Add
} else if(!(--(Prs->Mid->Deg))) Queue[++Tl] = Prs->Mid;//1st Add
} else {//Cur is C or B
if(Cur == Prs->Ri) {//Cur is C
if(Prs->Le->Vis) {//2nd or 3rd
if(!(Prs->Mid->Vis)) {if(Prs->Le->Le) --PutLeft; else ++PutLeft;}//2nd Add
} else if(!(--(Prs->Mid->Deg)))Queue[++Tl] = Prs->Mid; //1st Add
} else {//Cur is B
if(!((Prs->Ri->Vis) & (Prs->Le->Vis))) {//2nd Add
if(Prs->Ri->Vis) {if(Prs->Ri->Le) ++PutLeft;else --PutLeft;}//1st is C
else {if(Prs->Le->Le) ++PutLeft;else --PutLeft;}//1st is A
}
}
}
}
Cur->Le = (PutLeft >= 100000);
Ans[(PutLeft < 100000) ? (--BdR) : (++BdL)] = Cur - N;
}
for (unsigned i(1); i <= n; ++i) printf("%u ", Ans[i]);
return Wild_Donkey;
}
DAG 重链剖分
求一个字符串的字典序第 k 大的子序列的后 p 位.
建子序列自动机, 从后往前转移, 设 fi 为以第 i 个字符为起点有多少种子序列, DP 求出, 然后 DFS 查找即可找到对应子序列, 然后输出后 p 位.
2-SAT
n 个布尔变量, 每个变量拆成两个点, 表示 0/1, 有 m 个条件, 表达了两个变量取 0 或 1 的情况, 形如 x 取 0/1 或 y 取 0/1 有且只有一个成立.
针对 x 为 0 y 为 1 至少有一个成立的情况.
x 的 0 点向 y 的 0 点连边, 表示 x 取 0 时 y 取 0, 而 x 的 1 点向 y 的 1 点连边, 另外再连反向边, 以此类推.
对于另一种约束, 即两种情况出现至少一种, 则不连反向边.
对于 x 就是 0 这种钦定式约束, 直接将 x 的 1 向 0 连边, 这样就能代表 x 为 1 的情况不合法.
得到了一个有向图, 有向图中任何节点能到达的节点都是只要它本身发生则一定会发生的情况, 所以很显然一个 1 点不能到达它对应的 0 点, 否则这个点不合法.
得到的图进行缩点, 拓扑排序.
如果某个 1 点和对应的 0 点在同一个强连通分量内, 则无解.
对于不在一个强连通分量的 0 和 1, 选择拓扑序大的点所在的强连通分量, 如果这个强连通分量已经不选了, 则不合法.
这时可能会出现一种情况, 可能卡掉算法:
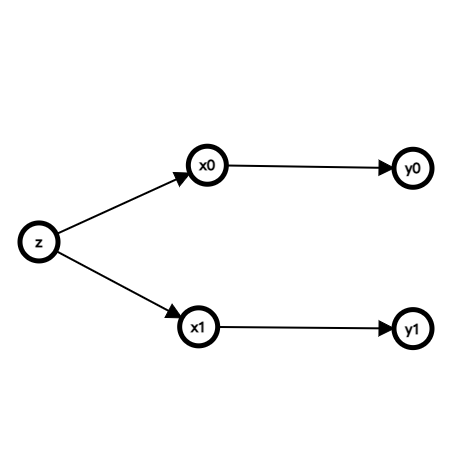
这时假设拓扑序为: Rankz=1, Rankx0=2, Rankx1=3, Ranky0=5, Ranky1=4
这时我们会得出 x1, y0 的答案, 不合法.
但是当我们重新审视这组数据, 发现不会存在仅从 x 的点往 y 的点连边的情况, 所以不会出现这种数据.
unsigned m, n, n2, Top(0), SCC(0);
unsigned A, B, C, D, t;
unsigned Cnt(0), Tmp(0);
unsigned Fa[2000005], SetStack[2000005], STop(0);
char Ans[1000005];
struct Node;
struct Edge {
Node* To;
Edge* Nxt;
}E[2000005], * CntE(E);
struct Node {
Edge* Fst;
unsigned Low, DFSr, Bel;
char InS;
}N[2000005], * Stack[2000005];
inline unsigned Find(unsigned x) {
while (x ^ Fa[x]) SetStack[++STop] = x, x = Fa[x];
while (STop) Fa[SetStack[STop--]] = x;
return x;
}
inline void Link(Node* x, Node* y) {
(++CntE)->Nxt = x->Fst, x->Fst = CntE, CntE->To = y;
Fa[Find(x - N)] = Find(y - N);
}
inline void Tarjan(Node* x) {
x->Low = x->DFSr = ++Cnt, Stack[++Top] = x, x->InS = 1;
Edge* Sid(x->Fst);
while (Sid) {
if(Sid->To->DFSr) {
if(Sid->To->InS) x->Low = min(x->Low, Sid->To->Low);
} else {
Tarjan(Sid->To), x->Low = min(x->Low, Sid->To->Low);
}
Sid = Sid->Nxt;
}
if(x->Low == x->DFSr) {
++SCC;
do Stack[Top]->Bel = SCC, Stack[Top]->InS = 0; while (Stack[Top--] != x);
}
}
signed main() {
n2 = ((n = RD()) << 1), m = RD();
for (unsigned i(1); i <= m; ++i) {
A = (RD() << 1), B = RD(), C = (RD() << 1), D = RD();
Link(N + (A ^ B ^ 1), N + (C ^ D));
Link(N + (C ^ D ^ 1), N + (A ^ B));
}
for (unsigned i(1); i <= n2; ++i) if(!N[i + 1].DFSr) Tarjan(N + i + 1);
for (unsigned i(2); i <= n2; i += 2) {
if(N[i ^ 1].Bel == N[i].Bel) {printf("IMPOSSIBLE\n");return 0;}
Ans[i >> 1] = (N[i ^ 1].Bel < N[i].Bel) ? 1 : 0;
}
printf("POSSIBLE\n");
for (unsigned i(1); i <= n; ++i) printf("%u ", Ans[i]);
return Wild_Donkey;
}
P6965 + LOJ6036
树链剖分优化建图, 复杂度 O(nlog2n), 开了 -O2 跑得真不慢.
有 n 个二进制串,每个串最多有一位是 ?。
你要给 ? 填上 0/1, 使得不存在 i, j 使 si 是 sj 的前缀.
洛谷上要输出方案, 而 LOJ 只需要判断可行性, 相当于弱化版, 所以这里只放 P6965 的做法.
将每个字符串 ? 取 0 和 1 的情况都存到 Trie 里.
我们发现, 如果选了一个节点, 那么它子树上的节点都不能选, 它到根的路径上的节点也不能选, 所以我们要往这些点的对应点上连边.
我们知道有线段树优化建边, 当线段树从序列上放到 Trie 上, 就需要树链剖分了, (显然我没有想到可以只连父子)
树链剖分建边是 O(nlog2n), 对于常数极大的线性算法, 这个算法增加的 log2n 的复杂度没有明显地比别的算法慢, 只是不开 -O2 会超时, 但是开了 -O2 便跑到了最优解第一页的前半部分.
建边之后跑 2-SAT 即可.
我觉得这份代码最妙的地方莫过于在递归过程中计算线段树区间长度, 然后用 vector 存图, 实现了线段树和有向图的无缝衔接, 这虽然对数组来说是很正常的事, 但是对于指针来说, 少定义两个结构体 (存边和存线段树) 确实大大减少了代码难度.
unsigned m, n, n2;
unsigned A, B, C, D, t;
unsigned Tmp(0);
unsigned DFSCnt(1), STop(0), SCC(0);
char TmpI[500005], UnSur[500005], Cr(0), Flg(0);
vector<char> Ans[500005];
struct Trie;
struct Node {
vector<Node*> To;
Trie* Tr;
unsigned Bel, Low, DFSr;
char InS;
}N[2000005], * List[2000005], * CntN, * Frm, * Root;
struct Trie {
Trie* Son[2], * Top, * Fa;
unsigned RL, RR, Size, Cnt;
char Heavy;
inline void PreDFS() {
unsigned Mx(0);
if (Son[0]) Son[0]->Fa = this, Son[0]->PreDFS(), Heavy = 0, Mx = Son[0]->Size;
if (Son[1]) {
Son[1]->Fa = this, Son[1]->PreDFS();
if (Son[1]->Size > Mx) Heavy = 1;
}
}
inline void DFS() {
RL = DFSCnt, RR = RL + Cnt - 1, DFSCnt += Cnt;
if (!Son[Heavy]) return;
Son[Heavy]->Top = Top, Son[Heavy]->DFS();
Trie* Cur(Son[Heavy ^ 1]);
if (Cur) Cur->Top = Cur, Cur->DFS();
}
}T[1000005], * CntT(T), * Lst1, * Lst2;
inline void Link(Node* x, unsigned L, unsigned R) {
if ((A <= L) && (R <= B)) { Frm->To.emplace_back(x);return; }
unsigned Mid((L + R) >> 1);
if (A <= Mid) Link(x->To[0], L, Mid);
if (B > Mid) Link(x->To[1], Mid + 1, R);
}
inline Node* Build(unsigned L, unsigned R) {
if (L == R) { return N + ((List[L] - N) ^ 1); }
unsigned Mid((L + R) >> 1);
Node* Cur(++CntN);
Cur->To.emplace_back(Build(L, Mid));
Cur->To.emplace_back(Build(Mid + 1, R));
return Cur;
}
inline void Tarjan(Node* x) {
x->DFSr = x->Low = ++DFSCnt, List[++STop] = x, x->InS = 1;
for (auto Cur : x->To) {
if (Cur->DFSr) { if (Cur->InS) x->Low = min(x->Low, Cur->Low); }
else Tarjan(Cur), x->Low = min(x->Low, Cur->Low);
}
if (x->DFSr == x->Low) {
++SCC;
do List[STop]->Bel = SCC, List[STop]->InS = 0;
while (List[STop--] != x);
}
}
signed main() {
CntN = N + (n2 = ((n = RD()) << 1)) - 1;
for (unsigned i(0), j(1); i < n; ++i) {
scanf("%s", TmpI + 1), Lst1 = Lst2 = T, j = 1;
while (TmpI[j] >= '0') {
++(Lst1->Size), ++(Lst2->Size);
Ans[i].push_back(TmpI[j]);
if (TmpI[j] == '?') {
UnSur[i] = 1;
if (!(Lst1->Son[0])) Lst1->Son[0] = ++CntT;
if (!(Lst2->Son[1])) Lst2->Son[1] = ++CntT;
Lst1 = Lst1->Son[0];
Lst2 = Lst2->Son[1];
}
else {
Cr = TmpI[j] - '0';
if (!(Lst1->Son[Cr])) Lst1->Son[Cr] = ++CntT;
if (!(Lst2->Son[Cr])) Lst2->Son[Cr] = ++CntT;
Lst1 = Lst1->Son[Cr];
Lst2 = Lst2->Son[Cr];
}
++j;
}
++(Lst1->Cnt), ++(Lst1->Size), N[i << 1].Tr = Lst1;
++(Lst2->Cnt), ++(Lst2->Size), N[(i << 1) ^ 1].Tr = Lst2;
}
T->PreDFS(), T->Top = T, T->DFS();
for (unsigned i(0); i < n2; ++i) List[(N[i].Tr)->RL + (--((N[i].Tr)->Cnt))] = N + i;
for (unsigned i(1); i <= n2; ++i) List[i]->DFSr = i;
Root = Build(1, n2);
for (Frm = N + n2 - 1; Frm >= N; --Frm) {
Trie* Cur(Frm->Tr);
A = Frm->DFSr + 1, B = Cur->RL + Cur->Size - 1;
if (A <= B) Link(Root, 1, n2);
A = Cur->Top->RL, B = Frm->DFSr - 1;
if (A <= B) Link(Root, 1, n2);
Cur = Cur->Top->Fa;
while (Cur) {
A = Cur->Top->RL, B = Cur->RR;
if (A <= B) Link(Root, 1, n2);
Cur = Cur->Top->Fa;
}
}
for (unsigned i(1); i <= n2; ++i) List[i]->DFSr = 0;
DFSCnt = 0, Tarjan(Root);
for (unsigned i(0); i < n; ++i)
if (N[i << 1].Bel == N[(i << 1) ^ 1].Bel) { Flg = 1;break; }
else UnSur[i] = (N[i << 1].Bel > N[(i << 1) ^ 1].Bel ? 1 : 0);
if (Flg) { printf("NO\n"); return 0; }
printf("YES\n");
for (unsigned i(0); i < n; ++i) {
for (auto j : Ans[i]) {
if (j == '?') putchar(UnSur[i] + '0');
else putchar(j);
}
putchar('\n');
}
return Wild_Donkey;
}
AT2336
数轴上插 n 面旗, 第 i 面要么插 xi, 要么插 yi. 使相邻旗子最小间隔最大.
设计每个旗子两个点分别表示选 xi 和 yi, 然后二分答案 Ans, 这样每个点 xi 左后各 Ans 位区间内的点的对应点都应该和 yi 连边, 跑 2-SAT 判断可行性.
用线段树优化建边, 线段树优化 Tarjan, 可以在 O(nlogn) 的时间内, 跑 O(n2) 条边的 Tarjan.
AC 之后才发现, 我写的根本就不是什么线段树优化建边, 如果非要起个名字, 我愿称之为 "无边Tarjan", 虽然常数效率不高, 但是实现非常精彩, 再次给线段树长脸了.
unsigned m, n, n2, SCC, Top(0);
unsigned A, B, C, D, t;
unsigned BinL(0), BinR(1000000000), BinMid;
unsigned Cnt(0), Ans(0), Tmp(0);
char Flg(0);
struct Node;
struct Seg;
struct Node {
Node* Bro;
unsigned RL, RR, Low, DFSr, Pos, Num, Bel;
inline const char operator < (const Node &x) const {return Pos < x.Pos; }
}N[20005], ForFind, * Tlag[10005], *Stack[20005], * To;
struct Seg {
Seg* LS, * RS;
Node* Ava;
unsigned Mn;
inline void Chg(unsigned L, unsigned R) {
if(L == R) {Mn = B;return;}
unsigned Mid((L + R) >> 1);
if(A <= Mid) LS->Chg(L, Mid);
else RS->Chg(Mid + 1, R);
Mn = min(LS->Mn, RS->Mn);
}
inline void Vis(unsigned L, unsigned R) {
if(L == R) {Ava = NULL;return;}
unsigned Mid((L + R) >> 1);
if(A <= Mid) LS->Vis(L, Mid);
else RS->Vis(Mid + 1, R);
Ava = (LS->Ava) ? (LS->Ava) : (RS->Ava);
}
inline void Qry(unsigned L, unsigned R) {
if((A <= L) && (R <= B)) {Ans = min(Ans, Mn);return;}
unsigned Mid((L + R) >> 1);
if(A <= Mid) LS->Qry(L, Mid);
if(B > Mid) RS->Qry(Mid + 1, R);
}
inline void Find(unsigned L, unsigned R) {
if((A <= L) && (R <= B)) {To = Ava;return;}
unsigned Mid((L + R) >> 1);
if(A <= Mid) LS->Find(L, Mid);
if(To) return;
if(B > Mid) RS->Find(Mid + 1, R);
}
}S[40005], * CntS(0);
inline void Build(Seg* x, unsigned L, unsigned R) {
x->Mn = 0x3f3f3f3f;
if (L == R) {x->Ava = N[L].Bro;return;}
unsigned Mid((L + R) >> 1);
Build(x->LS = ++CntS, L, Mid);
Build(x->RS = ++CntS, Mid + 1, R);
x->Ava = (x->LS->Ava) ? (x->LS->Ava) : (x->RS->Ava);
}
inline void Tarjan(Node* x) {
x->Low = x->DFSr = ++Cnt, Stack[++Top] = x;
Ans = 0x3f3f3f3f, A = x->RL, B = x - N - 1;
if((B < 0x3f3f3f3f) && (A <= B)) S->Qry(0, n2 - 1);
A = x + 1 - N, B = x->RR;
if(A <= B) S->Qry(0, n2 - 1);
x->Low = min(x->Low, Ans);
A = x->Bro - N, B = x->Low, S->Chg(0, n2 - 1), S->Vis(0, n2 - 1);
To = NULL, A = x->RL, B = x - N - 1;
if((B < 0x3f3f3f3f) && (A <= B)) S->Find(0, n2 - 1);
A = x + 1 - N, B = x->RR;
if(A <= B) S->Find(0, n2 - 1);
Node* Cur(To);
while(Cur) {
Tarjan(Cur), x->Low = min(x->Low, Cur->Low);
To = NULL, A = x->RL, B = x - N - 1;
if((B < 0x3f3f3f3f) && (A <= B)) S->Find(0, n2 - 1);
A = x + 1 - N, B = x->RR;
if(A <= B) S->Find(0, n2 - 1);
Cur = To;
}
A = x->Bro - N, B = x->Low, S->Chg(0, n2 - 1);
if(x->Low == x->DFSr) {
++SCC, B = 0x3f3f3f3f;
do{
A = Stack[Top]->Bro - N, S->Chg(0, n2 - 1), Stack[Top]->Bel = SCC;
}while(Stack[Top--] != x);
}
}
inline char Judge(unsigned x) {
SCC = 0, Flg = 0, CntS = S, Cnt = 0;
Build(S, 0, n2 - 1);
for (unsigned i(0); i < n2; ++i) {
if(N[i].Pos >= x) ForFind.Pos = N[i].Pos - x + 1, N[i].RL = lower_bound(N, N + n2, ForFind) - N;
else N[i].RL = 0;
ForFind.Pos = N[i].Pos + x, N[i].RR = lower_bound(N, N + n2, ForFind) - N;
if(N[i].RR >= n2) N[i].RR = n2 - 1; else --(N[i].RR);
}
for (unsigned i(0); i < n2; ++i) N[i].Low = N[i].DFSr = N[i].Bel = 0;
for (unsigned i(0); i < n2; ++i) if(!N[i].DFSr) Tarjan(N + i);
for (unsigned i(0); i < n2; ++i) if(N[i].Bel == N[i].Bro->Bel) {Flg = 1;break;}
return Flg;
}
signed main() {
n2 = ((n = RD()) << 1);
for (unsigned i(0); i < n2; i += 2) {
N[i].Pos = RD(), N[i ^ 1].Pos = RD();
N[i].Num = N[i ^ 1].Num = i >> 1;
}
sort(N, N + n2);
for (unsigned i(0); i < n2; ++i) {
if(Tlag[N[i].Num]) Tlag[N[i].Num]->Bro = N + i, N[i].Bro = Tlag[N[i].Num];
else Tlag[N[i].Num] = N + i;
}
while (BinL ^ BinR) {
BinMid = (BinL + BinR + 1) >> 1;
if(Judge(BinMid)) BinR = BinMid - 1;
else BinL = BinMid;
}
printf("%u\n", BinL);
return Wild_Donkey;
}
P6898
给定 n 个点的无向带权图, 将点集剖分成 L, R, 最小化 L 内部最大边权与 R 内部最大边权的和.
假设 L 的最大边权更大, 枚举 L 的最大边权 x, 二分 R 的最大边权 y. 对于一个二分到的 (x,y), 对所有大于 x 的边 (ui,vi), 连接 uiL 和 viR, 对于大于 y 的边, 连接 uiR 和 viL. 每次判断 x, y 是否可行可以直接跑 2-SAT, 单次 O(1).
但是这样的 2-SAT 判断次数达到了 O(n2logMax), 总复杂度 O(n4logMax), n≤200 是必然过不去的.
从大到小枚举边, 对于每条枚举的边, 假设它是 L 内部的最大边, 也就是 x. 然后讨论原图只选取 ≥x 的边, 得到的环的情况.
由于是从大到小枚举, 所以是不断向当前的图里加边, 而一条一条加边判断环的这种操作很经典的方法是并查集.
这里先定义一条边加入是否成环: 一条边加入后成环, 当且仅当它的两端本来就在一个连通块内.
接下来分类讨论按顺序枚举的边加入后成环情况:
-
不成环
这种情况直接二分 y, 统计答案即可.
-
成偶环
这时当前枚举的边的两端都应该在 L 中, 而如果这两个点都在 L 中, 剩下的点无论如何分配, 都会出现大于等于 x 的边连接同一集合内的两点, 所以这条边是不能做最大边的, 但是不排除更小的边做最大边的情况, 所以什么都不做直接
continue. -
成奇环
已经成奇环了, 奇环内无论怎么分配, 至少存在一条边会出现在集合内部, 我们设这条边是当前枚举的边, 这时 L 的最大边权是 x, 二分 y 得到这种情况的答案. 但是这时如果继续枚举边, 则这个奇环中的边都不能出现在集合内部了, 但是奇环永远不会消失, 所以以后就不会有解了, 所以二分完以后就结束枚举.
复杂度证明, 第一种情况的出现次数取决于两个端点不在一个集合中的边数, 容易发现, 第一种情况每次出现一次, 集合数就会少 1, 所以这种情况的出现次数是 O(n) 的. 每次出现花费 O(n2logMax) 的复杂度, 所以总复杂度 O(n3logMax).
第二种情况出现最多是 O(n2) 次, 这种情况可以通过二分图的形式连边来构造, 每次出现消耗 O(logn) 的复杂度, 总复杂度 O(n2logn).
第三种情况最多出现一次, 复杂度 O(n2logMax).
三种情况的总复杂度 O(n3logMax).
代码部分, 需要查询环的奇偶, 所以使用边带权并查集, 维护每条边成环情况. 对于二分判断, 直接常规 2-SAT 即可.
unsigned E[205][205], Stack[405];
unsigned DFSr[405], Low[405], Bel[405], Col[405];
unsigned Fa[205], Setak[205], STop(0);
unsigned m, n, n2;
unsigned A, B, C, D, Mx(0);
unsigned Cnt(0), SCC(0), Ans(0x3f3f3f3f), Tmp(0), Top(0);
unsigned char ToFa[205];
char InS[405], Flg(0);
struct Edge {
unsigned Frm, To, Val;
const inline char operator <(const Edge& x) const {return Val < x.Val;}
}List[20005];
inline void Tarjan(unsigned x) {
Low[x] = DFSr[x] = ++Cnt, Stack[++Top] = x, InS[x] = 1;
if(x & 1) {
for (unsigned i(0); i < n; ++i) {
if(E[x >> 1][i] > D) {
unsigned Cur(i << 1);
if (DFSr[Cur]) {if(InS[Cur]) Low[x] = min(Low[x], Low[Cur]);}
else Tarjan(Cur), Low[x] = min(Low[x], Low[Cur]);
}
}
}else {
for (unsigned i(0); i < n; ++i) {
if(E[x >> 1][i] > C) {
unsigned Cur((i << 1) ^ 1);
if (DFSr[Cur]) {if(InS[Cur]) Low[x] = min(Low[x], Low[Cur]);}
else Tarjan(Cur), Low[x] = min(Low[x], Low[Cur]);
}
}
}
if(Low[x] == DFSr[x]) {
++SCC;
do Bel[Stack[Top]] = SCC, InS[Stack[Top]] = 0;
while(Stack[Top--] ^ x);
}
}
inline char Judge () {
memset(Low, 0, ((n + 1) << 3));
memset(DFSr, 0, ((n + 1) << 3));
Cnt = 0, SCC = 0;
for (unsigned i(0); i < n2; ++i) if(!DFSr[i]) Tarjan(i);
for (unsigned i(0); i < n; ++i) if(Bel[i << 1] == Bel[(i << 1) ^ 1]) return 0;
return 1;
}
inline unsigned Find(unsigned x) {
unsigned char AddUp(0);
while (Fa[x] ^ x) Setak[++STop] = x, x = Fa[x];
while (STop) AddUp += ToFa[Setak[STop]], Fa[Setak[STop]] = x, ToFa[Setak[STop--]] = AddUp & 1;
return x;
}
inline void Binary() {
A = 0, B = D + 1;
while (A ^ B) {
C = (A + B) >> 1;
if(Judge()) B = C;
else A = C + 1;
}
if(A ^ (D + 1)) Ans = min(Ans, D + A);
}
signed main() {
n2 = ((n = RD()) << 1), m = (n * (n + 1)) >> 1;
for (unsigned i(0); i < n; ++i) Fa[i] = i;
for (unsigned i(0); i < n; ++i) {
E[i][i] = 0;
for (unsigned j(i + 1); j < n; ++j)
Mx = max(Mx, List[++Cnt].Val = E[i][j] = E[j][i] = RD()),
List[Cnt].Frm = i, List[Cnt].To = j;
List[++Cnt].Val = 0, List[Cnt].Frm = List[Cnt].To = i;
}
sort(List + 1, List + m + 1);
for (unsigned i(m); i; --i) {
D = List[i].Val, A = Find(List[i].Frm), B = Find(List[i].To);
if(A ^ B) {
Fa[A] = B, ToFa[A] = ToFa[List[i].Frm] ^ ToFa[List[i].To] ^ 1, Binary();
} else {
if(ToFa[List[i].Frm] ^ ToFa[List[i].To]) continue;
else {Binary();break;}
}
}
printf("%u\n", Ans);
return Wild_Donkey;
}
CF1215F
有 n 个电台, 频段在 [l(i),r(i)] 之间.
由你在 [1,m] 中选频段 f. 区间不包含 f 的电台不能被启用.
给 k 条限制, 有两种:
-
电台 u 和 v 至少选一个
-
电台 u 和 v 不能同时选
输出 f 和选择方案.
其实频段就是增加了一些不能同时选的限制, 所以理论上我们应该给区间不交的点连边, 但是这样显然是 O(n2) 的, 发现可以, 前缀和 + 后缀和优化建边, 优化到 O(nlogn).
得到的图跑 2-SAT.
得到一组可行解后, 将所有选定的区间取交 (其实就是求这些区间左端点最大值), 输出方案即可.
unsigned m, n, p, M;
unsigned A, B, C, D, t;
unsigned a[400005];
unsigned Cnt(0), Ans(0), Tmp(0), SCC(0), Top(0);
char Choice[400005], Flg(0);
struct Node;
struct Node {
vector<Node*> To;
unsigned DFSr, Low, Bel;
char InS;
}N[1600005], * Stack[1600005], * Suf, * Pref;
struct Station {
unsigned Le, Ri, Num;
inline const char operator<(const Station& x) const{ return Num < x.Num;}
}S[400005];
inline char Cmpl(const Station &x, const Station &y) {return x.Le < y.Le;}
inline char Cmpr(const Station &x, const Station &y) {return x.Ri < y.Ri;}
inline void Tarjan(Node* x) {
x->DFSr = x->Low = ++Cnt, Stack[++Top] = x, x->InS = 1;
for (auto i:x->To) {
if(i->DFSr) { if(i->InS) x->Low = min(x->Low, i->Low); }
else Tarjan(i), x->Low = min(x->Low, i->Low);
}
if(x->Low == x->DFSr) {
++SCC;
do Stack[Top]->Bel = SCC, Stack[Top]->InS = 0;
while (Stack[Top--] != x);
}
}
signed main() {
n = RD(), p = RD(), M = RD(), m = RD();
Suf = N + (p << 1) + 1, Pref = Suf + p;
for (unsigned i(1); i <= n; ++i)
A = RD() << 1, B = RD() << 1, N[A ^ 1].To.push_back(N + B), N[B ^ 1].To.push_back(N + A);
for (unsigned i(1); i <= p; ++i) S[i].Le = RD(), S[i].Ri = RD(), S[i].Num = i;
for (unsigned i(1); i <= m; ++i)
A = RD() << 1, B = RD() << 1, N[A].To.push_back(N + (B ^ 1)), N[B].To.push_back(N + (A ^ 1));
sort(S + 1, S + p + 1, Cmpl);
for (unsigned i(1); i <= p; ++i) Suf[i].To.push_back(N + ((S[i].Num << 1) ^ 1));
for (unsigned i(1); i < p; ++i) Suf[i].To.push_back(Suf + i + 1);
for (unsigned i(1); i <= p; ++i) a[i] = S[i].Le;
for (unsigned i(1); i <= p; ++i) {
A = upper_bound(a + 1, a + p + 1, S[i].Ri) - a;
if(A <= p) N[S[i].Num << 1].To.push_back(Suf + A);
}
sort(S + 1, S + p + 1, Cmpr);
for (unsigned i(1); i <= p; ++i) Pref[i].To.push_back(N + ((S[i].Num << 1) ^ 1));
for (unsigned i(2); i <= p; ++i) Pref[i].To.push_back(Pref + i - 1);
for (unsigned i(1); i <= p; ++i) a[i] = S[i].Ri;
for (unsigned i(1); i <= p; ++i) {
A = lower_bound(a + 1, a + p + 1, S[i].Le) - a - 1;
if(A) N[S[i].Num << 1].To.push_back(Pref + A);
}
for (Node* i(N + ((p << 1) ^ 1)); i > N + 1; --i) if(!(i->DFSr)) Tarjan(i);
for (unsigned i(1); i <= p; ++i)
if(N[i << 1].Bel ^ N[(i << 1) ^ 1].Bel) Choice[i] = N[i << 1].Bel < N[(i << 1) ^ 1].Bel;
else {Flg = 1; break;}
if(Flg) {printf("-1\n"); return 0;}
A = 0, B = 0x3f3f3f3f;
sort(S + 1, S + p + 1);
for (unsigned i(1); i <= p; ++i) if(Choice[i])
A = max(A, S[i].Le), ++Ans;
printf("%u %u\n", Ans, A);
for (unsigned i(1); i <= p; ++i) if(Choice[i]) printf("%u ", i);
return Wild_Donkey;
}
Day17: 网络流
Ford_Fulkerson
每次从源点 DFS 找增广路, 因为 DFS 可能会每次只找 1 个流量, 而且可能会遍历整个边集, 可能会被卡到 O(mMax).
Edmond_Karp
将 DFS 改成 BFS, 每次找边数最少的增广路来增广.
Dinic
BFS 将图分层, DFS 找增广路, 一次 DFS 走多条增广路. 为了避免走得太远, 选择只能从一个点走到它下一层的点. 复杂度 O(n2m)
其它算法
但是仅仅是 Dinic 还远远不够, Dinic 的常用优化 ISAP 综合常数和复杂度考虑往往是常规数据中最有效率的算法. 对于正解是网络流的题目, 95% 的题目可以用 Dinic 通过, 99.5% 的题目可以用 ISAP 通过.
但是因为 HLPP 的复杂度非常优秀, 所以在一些较大的数据中, HLPP 是竞赛中会用到的最高效的算法. 但是由于代码复杂度, 常数还有网络流算法一般不会跑到复杂度上界等原因, Dinic 仍是算法竞赛的首选, 而且不会被卡.
最小割
最小割大小即为最大流大小, 这便是最小割最大流定理.
最大权闭合子图
一个有向图, 选择一个点就必须选择其后继点. 求选择的总点权最大值.
假设初始全选所有正权点, 设这个总和为 Sum, 建 S 连向所有正权点, 负权点连向 T, 容量都是对应点权的绝对值, 求出最大流也就是最小割.
Sum 减掉最小割就是答案.
这样做正确性的保证是一开始假设所有的正权点都选了, 即 S 到正权点总容量为 Sum, 而所有负权点也都统计了, 但是统计的负权不会超过选择它所需要的正权点的点权和.
如果有的正权点使用入不敷出, 花费也顶多和收获相等, 这时总的收获中就会将这个点减去, 相当于没选.
如果有的点有富余, 那么总收获中减去它后继的负权就会剩下净赚.
所以我们的策略相当于将亏的正权点都不选, 只选有净赚的点.
最小费用最大流
从图上以 S 为起点按边权跑最短路, 然后沿最短路推流.
一般跑 Dinic, 就是用 SPFA 代替原来的 BFS 即可 (原来的最大流算法可以认为是这种算法使得网络边权都是 1, 回边边权是 −1).
无源汇上下界可行流
每条边有流量上下界, 求最大流.
新建超级源汇 SS, ST.
强制流满每条边的下界, 然后将每条边的容量设为 上界−下界.
如果某个点流量不平衡 (流出 ≠ 流入), 则往超级源汇连边.
流入多几个单位就从 SS 往这个点连几个单位容量的边;
流出多几个单位就从这个点往 ST 连几个单位容量的边.
这个时候, SS 出边容量和应该等于 TT 入边容量和.
跑 SS 到 ST 的最大流即可, 如果最大流小于 SS 的出边容量和或 TT 的入边流量和, 说明没有可行流, 否则每条边当前流量加上它的下界, 就是一组可行流中流经它的流量.
这样做的原因是对于流入 > 流出的点, 我们给它补上一个流量, 就可以给多出来的流量找到出路, 把积压的流量疏通出去;
对于流出 > 流入的点, 给它抽走这个流量, 就可以需求倒逼生产力发展, 为它收集缺少的流量.
而 SS 到 TT 的最大流等于 SS 出边总和说明积压的流量都被疏散了, 最大流等于 TT 入边总和说明需求的流量都被收集了.
有源汇上下界可行流
原来的 T 往 S 连下界为 0, 上界无穷的边, 在新的图上跑无源汇上下界可行流, 如果存在可行流, 则这个可行方案中, T 到 S 的边的流量便是 S 到 T 的可行流.
有源汇上下界最小流
跑一遍有源汇上下界可行流, 如果存在可行流, 删掉 SS, TT, 得到一张残量网络, 然后从 T 往 S 退流, 也就是跑最大流, 可行流减去这个最大流得到的就是答案.
有源汇上下界最大流
类似于有源汇上下界最小流, 可行流之后的操作改为从 S 向 T 推最大流即可.
上下界最小费用可行流
仍然是类似于普通可行流, 和 SS, ST 连边, 然后跑最小费用最大流, 统计出的可行流加权就是答案.
二分图匹配
匈牙利 O(mn), Dinic O(m√n).
过水已隐藏
二分图最大独立集
指图上找出最多的点使得点集中没有任何点之间有边.
二分图的最大独立集大小就是 n−最大匹配.
很好理解, 我们先全选, 然后对于每对匹配, 删除其中一个点即可.
二分图最大权匹配
边带权的二分图, 最大匹配可以认为是求一个最大的边的集合, 使得这些边的端点各不相同. 最大权匹配可以理解为在保证最大匹配的前提下使得边权和最大.
在最大流跑最大匹配的时候给边加权, 跑最小费用最大流 O(nm) 解决.
存在 DFS 的 O(n4) 的 KM 算法, 和基于 BFS 的 O(n3) 的 KM 算法, 后者比费用流高效.
Hall
如果二分图的最大匹配等于它点数较少的一侧的点数, 我们说这个二分图具有完美匹配.
将点数较少的一侧当作左部, 如果 S 表示左部点的任意点集, R(S) 表示所有 S 中的点直接连接的右部点点集.
根据 Hall 定理, 如果对所有 S, 都有 |R(S)|≥S, 则二分图有完美匹配.
P4001
给一个边带权网格图, 和一般网格图不同的是, 每个网格的左上角和右下角也有连边, 求左上角为源, 右下角为汇的路径上的最小割.
而网格图是一个平面图, 平面图是边两两不相交的图, 通俗地说, 可以画在平面上, 保证两两边不相交的图.
平面图的性质就是以每个边分割出来的区域为点, 相邻的区域之间连边, 边权就是跨过的那条网格图边的边权, 在新图上跑单源最短路即可得到原图的最小割. (原图汇到源连无穷大的边)
很遗憾, 有头铁的老哥实测本题网络流比最短路高效.
对于本题 106 的点, 3∗106 条边来说, 有些写法的 Dinic 可能无法通过, 很多人选择使用当前弧优化, 但是因为本题的图的特殊性, 可以就题论题地, 针对性地写出又短又快的代码, 在没有任何优化的情况下可以说是跑得飞快了.
const int Direc[12] = {-1005, 1005, -1, 1, -1006, 1006, -1005, 1005, -1, 1, -1006, 1006};
const unsigned char Inv[12] = {7, 6, 9, 8, 11, 10, 1, 0, 3, 2, 5, 4};
struct Node {
unsigned Edge[12], Dep;
}N[1005][1005], * Q[1000005];
unsigned a[10005], m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0);
unsigned Hd, Tl;
inline char BFS() {
Hd = Tl = 0, (Q[++Tl] = N[1] + 1)->Dep = 1;
while (Hd ^ Tl) {
Node* Cur(Q[++Hd]);
for (unsigned char i(0); i < 12; ++i) if(Cur->Edge[i]) {
Node* To(Cur + Direc[i]);
if(To->Dep >= 0x3f3f3f3f) To->Dep = Cur->Dep + 1, Q[++Tl] = To;
}
}
return N[n][m].Dep < 0x3f3f3f3f;
}
inline unsigned DFS(Node* x, const unsigned& Come) {
if(x == N[n] + m) {Ans += Come; return Come;}
unsigned Cur(Come);
for (unsigned char i(0); i < 12; ++i) if (x->Edge[i]) {
Node* To(x + Direc[i]);
if(To->Dep == x->Dep + 1) {
unsigned Push(min(x->Edge[i], Cur)), Tmp(DFS(To, Push));
if(Tmp < Push) To->Dep = 0x3f3f3f3f;
x->Edge[i] -= Tmp;
To->Edge[Inv[i]] += Tmp;
Cur -= Tmp;
if(!Cur) break;
}
}
return Come - Cur;
}
signed main() {
n = RD(), m = RD();
for (unsigned i(1); i <= n; ++i) for (unsigned j(1); j < m; ++j)
N[i][j].Edge[3] = N[i][j + 1].Edge[2] = RD();
for (unsigned i(1); i < n; ++i) for (unsigned j(1); j <= m; ++j)
N[i][j].Edge[1] = N[i + 1][j].Edge[0] = RD();
for (unsigned i(1); i < n; ++i) for (unsigned j(1); j < m; ++j)
N[i][j].Edge[5] = N[i + 1][j + 1].Edge[4] = RD();
for (unsigned i(n + 1); ~i; --i) for (unsigned j(m + 1); ~j; --j) N[i][j].Dep = 0x3f3f3f3f;
while (BFS()) {
DFS(N[1] + 1, 0x3f3f3f3f);
for (unsigned i(n + 1); ~i; --i) for (unsigned j(m + 1); ~j; --j) N[i][j].Dep = 0x3f3f3f3f;
}
printf("%u\n", Ans);
return Wild_Donkey;
}
p2762
n 个实验, m 个仪器, 每个实验用到的仪器是 m 个仪器的子集, 每个仪器可以用于多个实验, 每个实验有 ci 收益, 求如何安排实验, 使得去掉仪器花费后的净收益最大.
每个实验和仪器都视为点, 实验的权值为正, 是它的收益, 仪器的收益为负, 是它的花费.
每个实验向对应的仪器连容量无限的边, 然后建超级源汇 SS, ST, 将 SS 往实验上连边, 仪器的点往 ST 连边, 跑最大闭合子图即可.
这个题还有一个要求, 就是输出方案, 我们从 SS 开始 DFS, 遇到有余量的边就走, 所有能经过的实验都要选, 对应的能经过的仪器也要选.
unsigned m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0);
unsigned Hd, Tl;
char RDch, Prt[110];
struct Node;
struct Edge {
Node* To;
unsigned Cap, Inv;
Edge (Node* x, const unsigned &y) { To = x, Cap = y; }
Edge (Node* x) { To = x, Cap = 0; }
};
struct Node {
vector<Edge> Ed;
unsigned Dep;
}N[110], *Q[110], * E, * I;
inline unsigned RD() {
unsigned intmp(0);
RDch = getchar();
while (RDch < '0' || RDch > '9') RDch = getchar();
while (RDch >= '0' && RDch <= '9')
intmp = (intmp << 3) + (intmp << 1) + RDch - '0', RDch = getchar();
return intmp;
}
inline char BFS() {
Hd = Tl = 0, (Q[++Tl] = N)->Dep = 1;
while (Hd ^ Tl) {
Node* Cur(Q[++Hd]);
for (unsigned i(Cur->Ed.size() - 1); ~i; --i)
if((Cur->Ed[i].Cap) && (Cur->Ed[i].To->Dep >= 0x3f3f3f3f))
Q[++Tl] = Cur->Ed[i].To, Cur->Ed[i].To->Dep = Cur->Dep + 1;
}
return (N[1].Dep < 0x3f3f3f3f);
}
inline unsigned DFS(Node* x, const unsigned& Come) {
if(x == N + 1) {Ans -= Come; return Come;}
unsigned Cur(Come);
for (unsigned i(x->Ed.size() - 1); ~i; --i)
if((x->Ed[i].Cap) && (x->Ed[i].To->Dep == x->Dep + 1)) {
unsigned Go(min(Cur, x->Ed[i].Cap)), Push(DFS(x->Ed[i].To, Go));
if(Push < Go) x->Ed[i].To->Dep = 0x3f3f3f3f;
Cur -= Push, x->Ed[i].Cap -= Push, x->Ed[i].To->Ed[x->Ed[i].Inv].Cap += Push;
if (!Cur) break;
}
return Come - Cur;
}
inline void SufDFS (Node* x) {
Prt[x - N] = 1;
for (auto i:x->Ed) if((i.Cap) && (!Prt[i.To - N])) SufDFS(i.To);
}
signed main() {
E = N + 1, I = E + (m = RD()), n = RD();
for (unsigned i(1); i <= m; ++i) {
Ans += (A = RD());
N[0].Ed.push_back(Edge(E + i, A)), E[i].Ed.push_back(Edge(N));
N[0].Ed.back().Inv = E[i].Ed.size() - 1;
E[i].Ed.back().Inv = N[0].Ed.size() - 1;
while (RDch > 0x0d) {
A = RD();
E[i].Ed.push_back(Edge(I + A, 0x3f2f2f2f)), I[A].Ed.push_back(Edge(E + i));
E[i].Ed.back().Inv = I[A].Ed.size() - 1;
I[A].Ed.back().Inv = E[i].Ed.size() - 1;
}
}
for (unsigned i(1); i <= n; ++i) {
I[i].Ed.push_back(Edge(N + 1, RD())), N[1].Ed.push_back(Edge(I + i));
I[i].Ed.back().Inv = N[1].Ed.size() - 1;
N[1].Ed.back().Inv = I[i].Ed.size() - 1;
}
for (Node* i(I + n); i > N; --i) i->Dep = 0x3f3f3f3f;
while (BFS()) {
DFS(N, 0x3f3f3f3f);
for (Node* i(I + n); i > N; --i) i->Dep = 0x3f3f3f3f;
}
SufDFS(N);
for (unsigned i(1); i <= m; ++i) if(Prt[i + 1]) {printf("%u ", i);}
putchar(0x0A);
for (unsigned i(1); i <= n; ++i) if(Prt[1 + m + i]) printf("%u ", i);
putchar(0x0A);
printf("%u\n", Ans);
return Wild_Donkey;
}
P2763
n 道题, 每道题属于至少一种类型, 要求选 ∑mi 道题组卷, 每个类型要求存在 mi 道题, 求一组可行方案.
每个题是一个点, 向汇点连容量为 1 的边, 每个类型类型是一个点, 从源点连一条容量 mi 的边, 每个点分别向对应类型连边, 跑最大流, 有解当且仅当每条从源点出来的边满流, 而有流从一个类型流向一道题, 则这道题属于方案中的这个类型.
unsigned m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
struct Node;
struct Edge {
Node* To;
unsigned Val, Inv;
Edge (Node* x, const unsigned& y) {To = x, Val = y;}
Edge (Node* x) {To = x;}
};
struct Node {
vector<Edge> Ed;
unsigned Dep;
}N[1105], * Q[1105], * P, * T;
inline char BFS() {
for (Node* i(N); i <= T; ++i) i->Dep = 0x3f3f3f3f;
unsigned Hd(0), Tl(0);
(Q[++Tl] = N)->Dep = 1;
while (Hd ^ Tl) {
Node* Cur(Q[++Hd]);
for (auto i:Cur->Ed) if((i.Val) && (i.To->Dep >= 0x3f3f3f3f)) {
(Q[++Tl] = i.To)->Dep = Cur->Dep + 1;
}
}
return T->Dep < 0x3f3f3f3f;
}
inline unsigned DFS (Node* x, unsigned Come) {
if (x == T) {Ans -= Come; return Come;}
unsigned Res(Come);
for (unsigned i(x->Ed.size() - 1); ~i; --i)
if((x->Ed[i].Val) && (x->Ed[i].To->Dep == x->Dep + 1)){
unsigned Go(min(Res, x->Ed[i].Val)), Push(DFS(x->Ed[i].To, Go));
if(Push ^ Go) x->Ed[i].To->Dep = 0x3f3f3f3f;
Res -= Push, x->Ed[i].Val -= Push, x->Ed[i].To->Ed[x->Ed[i].Inv].Val += Push;
if(!Res) break;
}
return Come - Res;
}
signed main() {
P = N + (m = RD()), T = P + (n = RD()) + 1;
for (unsigned i(1); i <= m; ++i) {
N->Ed.push_back(Edge(N + i, RD()));
N[i].Ed.push_back(Edge(N + i));
N->Ed.back().Inv = N[i].Ed.size() - 1;
N[i].Ed.back().Inv = N->Ed.size() - 1;
Ans += N->Ed.back().Val;
}
for (unsigned i(1); i <= n; ++i) {
for (unsigned j(RD()); j; --j) {
A = RD();
N[A].Ed.push_back(Edge(P + i, 1));
P[i].Ed.push_back(Edge(N + A));
N[A].Ed.back().Inv = P[i].Ed.size() - 1;
P[i].Ed.back().Inv = N[A].Ed.size() - 1;
}
P[i].Ed.push_back(Edge(T, 1));
T->Ed.push_back(Edge(P + i));
T->Ed.back().Inv = P[i].Ed.size() - 1;
P[i].Ed.back().Inv = T->Ed.size() - 1;
}
while (BFS()) DFS(N, 0x3f3f3f3f);
if(Ans) {printf("No Solution!\n"); return 0;}
for (unsigned i(1); i <= m; ++i) {
printf("%u:", i);
for (auto j:N[i].Ed) if((!(j.Val)) && (j.To > P)) printf(" %u", j.To - P);
putchar(0x0A);
}
return Wild_Donkey;
}
P2764
有向图, 分成若干路径, 每条路径是简单路径且顶点不相交. 求一个划分方案使路径数量尽可能小.
一个划分合法的条件是每个点至多有一个出度, 最多有一个入度, 所以我们只要一个点拆成两个, 一个代表出度, 在左部, 一个代表入度, 在右部. 跑二分图最大匹配即可.
unsigned m, n, n2;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
unsigned char Nxt[155], Pre[155];
struct Node;
struct Edge {
Node* To;
unsigned char Val, Inv;
Edge (Node* x, const unsigned char& y) {To = x, Val = y;}
Edge (Node* x) {To = x, Val = 0;}
};
struct Node {
vector<Edge> Ed;
unsigned Dep;
}N[305], * Q[305];
inline char BFS() {
for (Node* i(N + n2 + 1); i > N; --i) i->Dep = 0x3f3f3f3f;
unsigned Hd(0), Tl(0);
(Q[++Tl] = N)->Dep = 1;
while (Hd ^ Tl) {
Node* Cur(Q[++Hd]);
for (auto i:Cur->Ed) if((i.Val) && (i.To->Dep >= 0x3f3f3f3f))
Q[++Tl] = i.To, i.To->Dep = Cur->Dep + 1;
}
return N[1].Dep < 0x3f3f3f3f;
}
inline char DFS(Node* x, unsigned char Come) {
if(x == N + 1) {--Ans; return 1;}
unsigned char Res(Come);
for (unsigned i(x->Ed.size() - 1); ~i; --i)
if((x->Ed[i].To->Dep == x->Dep + 1) && (x->Ed[i].Val)) {
unsigned char Push(DFS(x->Ed[i].To, 1));
if(!Push) { x->Ed[i].To->Dep = 0x3f3f3f3f; continue;}
--(x->Ed[i].Val), --Res, ++(x->Ed[i].To->Ed[x->Ed[i].Inv].Val);
if(!Res) break;
}
return Come - Res;
}
signed main() {
n2 = ((Ans = n = RD()) << 1) + 1, m = RD();
for (unsigned i(2); i <= n2; i += 2) {
N->Ed.push_back(Edge(N + i, 1));
N[i].Ed.push_back(Edge(N));
N->Ed[(i >> 1) - 1].Inv = 0;
N[i].Ed[0].Inv = (i >> 1) - 1;
}
for (unsigned i(3); i <= n2; i += 2) {
N[1].Ed.push_back(Edge(N + i));
N[i].Ed.push_back(Edge(N + 1, 1));
N[1].Ed[(i >> 1) - 1].Inv = 0;
N[i].Ed[0].Inv = (i >> 1) - 1;
}
for (unsigned i(1); i <= m; ++i) {
A = RD() << 1, B = (RD() << 1) ^ 1;
N[A].Ed.push_back(Edge(N + B, 1));
N[B].Ed.push_back(Edge(N + A));
N[A].Ed.back().Inv = N[B].Ed.size() - 1;
N[B].Ed.back().Inv = N[A].Ed.size() - 1;
}
while (BFS()) DFS(N, 0xff);
for (unsigned i(2); i <= n2; i += 2)
for (auto j:N[i].Ed) if((j.To > N) && (!(j.Val))) {
Nxt[i >> 1] = (j.To - N) >> 1, Pre[(j.To - N) >> 1] = 1; break;
}
for (unsigned char i(1), j; i <= n; ++i) {
if(!Pre[i]) {
j = i;
while (j) printf("%u ", j), j = Nxt[j];
putchar(0x0A);
}
}
printf("%u\n", Ans);
return Wild_Donkey;
}
P2765
n 个栈, 依次将正整数压入栈中, 要求栈中任何相邻数字的和为完全平方数. 计算最多压入多少数, 并且给出方案.
二分答案, 暴力枚举所有相加为完全平方数的数连边, 从小到大连单向边.
判断答案可行的时候统计图上的路径条数, 这样就和上一题一样, 每次判断求一下 DAG 的最小路径覆盖即可.
unsigned n, n2, Sq[65];
unsigned A, B, C, D, t;
unsigned Nxt[1605];
unsigned Cnt(0), Ans(0), Tmp(0);
unsigned char Idg[1605];
struct Node;
struct Edge {
Node* To;
unsigned Inv;
unsigned char Cap;
Edge (Node* x, const unsigned char y) {To = x, Cap = 1;}
Edge (Node* x) {To = x, Cap = 0;}
};
struct Node {
vector<Edge> E;
unsigned Dep;
}N[3205], * Q[3205], * Fr, * Th;
inline void Clr() {
n2 = ((Ans = C) << 1) ^ 1;
for (Node* i(N + n2); i >= N; --i) i->E.clear();
}
inline char BFS() {
for (Node* i(N + n2); i > N; --i) i->Dep = 0x3f3f3f3f;
unsigned Hd(0), Tl(0);
(Q[++Tl] = N)->Dep = 1;
while (Tl ^ Hd) {
Node* Cur(Q[++Hd]);
for (auto i:Cur->E) if((i.Cap) && (i.To->Dep >= 0x3f3f3f3f))
i.To->Dep = Cur->Dep + 1, Q[++Tl] = i.To;
}
return N[1].Dep < 0x3f3f3f3f;
}
inline unsigned char DFS(Node* x, unsigned Come) {
if(x == N + 1) { --Ans; return 1; }
unsigned Res(Come);
for (unsigned i(x->E.size() - 1); ~i; --i)
if((x->E[i].Cap) && (x->E[i].To->Dep == x->Dep + 1)) {
unsigned char Push(DFS(x->E[i].To, 1));
if(!Push) {x->E[i].To->Dep == 1; continue;}
--Res, --(x->E[i].Cap), ++(x->E[i].To->E[x->E[i].Inv].Cap);
if(!Res) break;
}
return Res < Come;
}
inline void Judge () {
for (unsigned i(2); i <= n2; i += 2) {
N[0].E.push_back(Edge(N + i, 1));
N[i].E.push_back(Edge(N));
N[0].E[(i >> 1) - 1].Inv = 0;
N[i].E[0].Inv = (i >> 1) - 1;
}
for (unsigned i(3); i <= n2; i += 2) {
N[1].E.push_back(Edge(N + i));
N[i].E.push_back(Edge(N + 1, 1));
N[1].E[(i >> 1) - 1].Inv = 0;
N[i].E[0].Inv = (i >> 1) - 1;
}
for (unsigned i(1); i <= C; ++i) {
Fr = N + (i << 1);
for (unsigned j(2); Sq[j] <= C + i; ++j) if((i << 1) < Sq[j]) {
Th = N + (((Sq[j] - i) << 1) ^ 1);
Fr->E.push_back(Edge(Th, 1));
Th->E.push_back(Edge(Fr));
Fr->E.back().Inv = Th->E.size() - 1;
Th->E.back().Inv = Fr->E.size() - 1;
}
}
while (BFS()) DFS(N, 0x3f3f3f3f);
}
signed main() {
n = RD();
A = 1, B = 1600;
for (unsigned i(1); i <= 60; ++i) Sq[i] = i * i;
while (A ^ B) {
C = (A + B + 1) >> 1, Clr(), Judge();
if(Ans > n) B = C - 1;
else A = C;
}
printf("%u\n", C = A);
Clr(), Judge();
for (Node* i(N + n2 - 1); i > N; i -= 2)
for (auto j:i->E) if((j.To > N) && (!(j.Cap)))
Nxt[(i - N) >> 1] = (j.To - N) >> 1, Idg[(j.To - N) >> 1] = 1;
for (unsigned i(1), j; i <= A; ++i) if(!(Idg[i])) {
j = i;
while (j) printf("%u ", j), j = Nxt[j];
putchar(0x0A);
}
return Wild_Donkey;
}
P2766
给一个序列.
-
计算最长不降子序列长度 s
-
求最多同时取出多少长度为 s 的不下降子序列
-
如果第一个和最后一个元素可以随意无限使用, 求最多同时取出多少长度为 s 的不同的不下降子序列
对于第一个问题, 直接 DP 即可.
设 DP 时每个点为结尾的最长不下降子序列为 fi.
第二个问题, 每个点拆成两个, 中间连一条容量为 1 的边, 自己的第二个点往自己后面不比自己小的数 j 并且 fj=fi+1 的第一个点连边, 这样就得到了一个分层图.
新建源点 S, 向每个深度为 1 的点连边, 新建汇点 T, 每个深度为 s 的点向汇点连边.
为了防止一个点两次被用, 我们将一个点拆成两个点, 中间用容量为 1 的边连接, 这样再跑最大流即可.
第三个问题, 为了复用第一个和最后一个元素, 我们只要将这两个元素的点之间的边, S 到 1 的第一个点, n 的第二个点到 T 的边的容量都设为无限.
别忘了特判序列长度为 1 的情况.
const unsigned maxn(1010);
unsigned Q[1005], Hd(0), Tl(0);
unsigned n, x[maxn], en(1), fst[maxn], S, T;
unsigned long long dep[maxn], Flow, Tmp1, Tmpn, Tmp, f[maxn], s;
struct Edge {
ll c;
unsigned to, nxt;
char Type;
}ed[maxn * maxn + maxn * 2];
void add(int u, int v, ll w) {
ed[++en].to = v, ed[en].c = w, ed[en].nxt = fst[u], fst[u] = en;
ed[++en].to = u, ed[en].nxt = fst[v], fst[v] = en;
}
bool BFS() {
memset(dep, 0, sizeof(dep));//重置深度
dep[S] = 1;//重新来过
Hd = Tl = 0, Q[++Tl] = S;
while (Tl ^ Hd) {//手写队列可不可以/kk
unsigned u(Q[++Hd]);
for (unsigned e(fst[u]), v(ed[e].to); e; e = ed[e].nxt, v = ed[e].to)
if ((!(dep[v])) && (ed[e].c > 0)) dep[v] = dep[u] + 1, Q[++Tl] = v;
}
return dep[T];
}
ll DFS(int u, ll flow) {//DFS 大成功 √
if (u == T) return flow;//汇点, 来多少要多少
if (!flow) return 0;//没有流量, 拉倒
ll res = flow;//分配
for (int e(fst[u]), v(ed[e].to); e; e = ed[e].nxt, v = ed[e].to) {
if (!res) break;
if ((dep[v] == dep[u] + 1) && (ed[e].c)) {//加个括号吧姐姐
ll k(DFS(v, min(res, ed[e].c)));//实际上的流量
if (!k) dep[v] = 0;//一点都流不得了
res -= k;
ed[e].c -= k, ed[e ^ 1].c += k;
}
}
return flow - res;//这时剩余的和进来的差就是实际流量
}
int main() {
n = rd(); S = n * 2 + 3, T = n * 2 + 4;
if (n == 1) { printf("1\n1\n1\n");return 0; }
for (int i(1); i <= n; ++i) x[i] = rd(), f[i] = 1;//2 ~ 2 * n + 1 // 自边 每一个点拆成两个点 二者连边? 用于限制每个数的使用次数
for (int i(1); i <= n; ++i) for (int j(1); j < i; ++j)
if (x[j] <= x[i]) f[i] = max(f[i], f[j] + 1);//DP 求最长
for (int i(1); i <= n; ++i) s = max(s, f[i]);
printf("%lld\n", s);
for (int i(1); i <= n; ++i) if (f[i] == 1) add(S, i, 1);
for (int i(1); i <= n; ++i) if (f[i] == s) add(i + n, T, 1);
for (int i(1); i <= n; ++i) for (int j(1); j < i; ++j)
if ((x[j] <= x[i]) && (f[j] + 1 == f[i])) add(j + n, i, 1);
for (int i(1); i <= n; ++i) add(i, i + n, 1);//自边
while (BFS()) Flow += DFS(S, inf); // 最大流
printf("%lld\n", Flow);
for (unsigned i(1); i <= en; ++i) ed[i].c = ((i & 1) ^ 1);
for (unsigned e(fst[S]); e; e = ed[e].nxt) if (ed[e].to == 1) ed[e].c = inf;
for (unsigned e(fst[n << 1]); e; e = ed[e].nxt) if (ed[e].to == T) ed[e].c = inf;
ed[fst[1]].c = inf, ed[fst[n]].c = inf, Flow = 0;
while (BFS()) Flow += DFS(S, inf); // 最大流
printf("%lld\n", Flow);
return 0;
}
P2774
给一个方格图, 每个格子有权值, 要求选出互不相邻的格子使得权值和最大, 求权值.
先在每对相邻的点之间连边, 得到一个二分图, 建立源点 S 连向二分图每个左部点一条容量为点权的边, 左部点到右部点的边容量无穷, 右部点向汇点 T 连容量为点权的边.
求这个网络的最小割后, 发现一定是 S 到左部点和右部点到 T 的边被割掉.
假设一开始选择所有点, 把每条边被割掉看成是对应的点被删除, 则最小割割掉后, 相当于不存在一条左右部之间的边两端的点都没有删掉的情况, 也就是点的选择合法了.
接下来分析其点权和最大, 因为是从所有点中, 删除一些点使得方案合法, 所以只要保证删除点权和最小, 而这个值等于网络的割, 因为求的是最小割, 所以这个值最小, 保证了答案正确性.
unsigned m, n, mn;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
struct Node;
struct Edge {
Node* To;
unsigned Cap, Inv;
};
struct Node {
vector<Edge> E;
unsigned Dep;
}N[10005], * Q[10005];
inline char BFS() {
for (Node* i(N + mn); i > N; --i) i->Dep = 0x3f3f3f3f;
unsigned Hd(0), Tl(0);
(Q[++Tl] = N)->Dep = 1;
while (Hd ^ Tl) {
Node* Cur(Q[++Hd]);
for (auto i:Cur->E) if((i.Cap) && (i.To->Dep >= 0x3f3f3f3f))
i.To->Dep = Cur->Dep + 1, Q[++Tl] = i.To;
}
return N[1].Dep < 0x3f3f3f3f;
}
inline unsigned DFS(Node* x, unsigned Come) {
if(x == N + 1) {Ans -= Come; return Come;}
unsigned Res(Come);
for (unsigned i(x->E.size() - 1); ~i; --i)
if((x->E[i].Cap) && (x->E[i].To->Dep == x->Dep + 1)) {
unsigned Go(min(x->E[i].Cap, Res)), Push(DFS(x->E[i].To, Go));
if(Push < Go) {x->E[i].To->Dep = 0x3f3f3f3f;}
Res -= Push, x->E[i].Cap -= Push, x->E[i].To->E[x->E[i].Inv].Cap += Push;
}
return Come - Res;
}
inline void Link(Node* x, Node* y) {
x->E.push_back((Edge){y, 0x3f3f3f3f, 0});
y->E.push_back((Edge){x, 0, 0});
x->E.back().Inv = y->E.size() - 1;
y->E.back().Inv = x->E.size() - 1;
return;
}
signed main() {
n = RD(), m = RD(), mn = (n * m) + 1;
for (unsigned i(1), k(2); i <= n; ++i) {
for (unsigned j(1); j <= m; ++j, ++k) {
Ans += (A = RD());
if((i ^ j) & 1) {
N->E.push_back((Edge){N + k, A, 0});
N[k].E.push_back((Edge){N, 0, 0});
N[k].E[0].Inv = (k >> 1) - 1;
} else {
N[1].E.push_back((Edge){N + k, 0, 0});
N[k].E.push_back((Edge){N + 1, A, 0});
N[k].E[0].Inv = (k >> 1) - 1;
}
}
}
for (unsigned i(2), j; i <= mn; ++i)
if (((((i - 2) / m) + 1) ^ (((i - 2) % m) + 1)) & 1) {
if ((i - 2) % m) Link(N + i, N + i - 1);
if ((i - 1) % m) Link(N + i, N + i + 1);
if (i > m + 1) Link(N + i, N + i - m);
if (i + m <= mn) Link(N + i, N + i + m);
}
while (BFS()) DFS(N, 0x3f3f3f3f);
printf("%u\n", Ans);
return Wild_Donkey;
}
由于在 vector 里只有 0 号元素的时候访问 1 号元素, 所以调了很久, 但是非常感谢小黄鸭的支持, 让我意识到这个问题, 获得了 AC.
P1251
有 n 天, 每天需要 ri 块餐巾, 每天可以送去快/慢洗部一些餐巾, 花费一定 morn 天是间和 fors 金钱洗完, 也可以新买一批餐巾, 花费金钱 p 立刻得到餐巾.
求保证每天有足够干净餐巾的情况下的最小花费.
每天建两个点, 分别是臭抹布点和新抹布点.
源点 S 向每天的新抹布点连一条费用为 p, 容量无限的边, 这些边代表着新抹布收费不限量供应.
源点 S 向每天的臭抹布点连一条免费的, 容量为 ri 的边, 表示臭抹布免费限量供应, 数量取决于当天用多少.
每天的新抹布点向汇点 T 连一条免费的, 容量为 ri 的边, 表示新抹布用完后扔到一个高维空间, 这里面的臭抹布会通过源点提供给当天的臭抹布点.
每天的臭抹布点下一天的臭抹布点连一条免费的, 容量无限的边, 表示可以把臭抹布放着不洗.
臭抹布点还可以向 n 或 m 天之后的新抹布点连费用为 s 或 f, 容量无限的边, 表示可以洗抹布.
容易发现, 这个网络最大流是所有天的抹布总和, 而它的最小费用最大流就是最小的花费.
#define INF 20000000000
long long a[4005];
long long QC, New, SC, Ans(0);
unsigned QD, SD, n, n2;
unsigned A, B, C, D, t;
unsigned Cnt(0);
struct Node;
struct Edge {
Node* To;
long long Val, Cap;
unsigned Inv;
};
struct Node {
vector<Edge> E;
long long Dis;
char InQ;
}N[4005], * Q[100005];
inline void Link(Node* x, Node* y, long long V) {
x->E.push_back((Edge){y, V, INF, 0});
y->E.push_back((Edge){x, -V, 0, 0});
x->E.back().Inv = y->E.size() - 1;
y->E.back().Inv = x->E.size() - 1;
}
inline char SPFA () {
for (Node* i(N + n2); i > N; --i) i->Dis = INF, i->InQ = 0;
unsigned Hd(0), Tl(0);
(Q[++Tl] = N)->Dis = 0, N->InQ = 1;
while (Hd ^ Tl) {
Node* Cur(Q[++Hd]);
Cur->InQ = 0;
for (auto i:Cur->E) if((i.Cap) && (i.To->Dis > Cur->Dis + i.Val)) {
i.To->Dis = Cur->Dis + i.Val;
if(!(i.To->InQ)) Q[++Tl] = i.To, i.To->InQ = 1;
}
}
return N[1].Dis < INF;
}
inline long long DFS (Node* x, long long Come) {
x->InQ = 1;
if(x == N + 1) {Ans += Come * x->Dis;return Come;}
long long Res(Come);
for (unsigned i(x->E.size() - 1); ~i; --i)
if((x->E[i].Cap) && (x->E[i].To->Dis == x->Dis + x->E[i].Val) && (!(x->E[i].To->InQ))) {
long long Go(min(x->E[i].Cap, Res)), Push(DFS(x->E[i].To, Go));
x->E[i].To->InQ = 0;
if(Go > Push) x->E[i].To->Dis = INF;
Res -= Push, x->E[i].Cap -= Push, x->E[i].To->E[x->E[i].Inv].Cap += Push;
if(!Res) break;
}
return Come - Res;
}
signed main() {
n2 = ((n = RD()) << 1) + 1;
for (unsigned i(1); i <= n; ++i) a[i] = RD();
New = RD(), QD = RD(), QC = RD(), SD = RD(), SC = RD();
for (unsigned i(2); i <= n2; i += 2) {
N->E.push_back((Edge){N + i, 0, a[i >> 1], 0});
N[i].E.push_back((Edge){N, 0, 0, (i >> 1) - 1});
}
for (unsigned i(3); i <= n2; i += 2) {
N->E.push_back((Edge){N + i, New, INF, 0});
N[i].E.push_back((Edge){N, -New, 0, n + (i >> 1) - 1});
}
for (unsigned i(3); i <= n2; i += 2) {
N[1].E.push_back((Edge){N + i, 0, 0, 1});
N[i].E.push_back((Edge){N + 1, 0, a[i >> 1], (i >> 1) - 1});
}
for (unsigned i(4); i <= n2; i += 2) Link(N + i - 2, N + i, 0);
if(QD < n) for (unsigned i(n2 - ((QD) << 1) ^ 1); i >= 2; i -= 2) Link(N + i, N + i + (QD << 1) + 1, QC);
if(SD < n) for (unsigned i(n2 - ((SD) << 1) ^ 1); i >= 2; i -= 2) Link(N + i, N + i + (SD << 1) + 1, SC);
while (SPFA()) DFS(N, INF);
printf("%lld\n", Ans);
return Wild_Donkey;
}
NOI2008
n 类志愿者, 每类可以在 [li,ri] 日期工作, 价格 ci. 每天需要 ai 个志愿者, 求满足所有条件的志愿者数量的最小花费.
这个题最恶心的地方有两点, 一点是一个人可以工作好几天, 这一点和上一题的餐巾可以洗净类似, 但是餐巾可以无限次洗净, 人却只能在特定的几天内工作. 第二点是每天的工作人数不一定非要和限制相等, 也可以有更多人在这一天工作.
这个题的建图也很神, 首先建立 n+1 个点, S 向 1 连免费容量无限的边, 然后 n+1 向 T 容量无限的边.
我们希望使得 S 到 T 的最大流是 INF, 并且在过程中对某些流进行收费, 令这些收费等于雇佣人的收费.
对于 i 到 i+1 的边, 使它们免费, 表示这些流量不是雇佣的人. 既然需要收费, 那么这些边的容量必然不能是 INF, 否则所有流就都从这些边流走了.
使 i 到 i+1 的边容量为 INF−ai, 其中缺失的 ai 流量需要被收费, 但是没有规定在哪收费, 所以只要有 ai 流量 (除了走免费边的 INF−ai 流以外) 从 i 以及 i 之前流向 i+1 以及 i+1 之后即可.
接下来是收费边, 一种人可以解决 [li,ri] 的缺人问题, 作为 li 到 ri+1 的免费边的流量补充, 这之间的所有边都能被这条边的收费所补充, 因此从 li 到 ri+1 连费用 ci, 容量无穷的边.
在这个网络上跑最小费用最大流即可.
#define INF 2147483647
#define IINF 0x3f3f3f3f3f3f3f3f
long long Ans(0);
unsigned a[1005], m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Tmp(0);
struct Node;
struct Edge {
Node* To;
int Val;
unsigned Cap, Inv;
};
struct Node {
vector<Edge> E;
long long Dis;
char InQ;
}N[1005], * Q[1000005];
inline void Link (Node* x, Node* y, const int& z) {
x->E.push_back((Edge){y, z, INF, 0});
y->E.push_back((Edge){x, -z, 0, 0});
x->E.back().Inv = y->E.size() - 1;
y->E.back().Inv = x->E.size() - 1;
};
inline char SPFA () {
unsigned Hd(0), Tl(0);
for (Node* i(N + n + 2); i > N; --i) i->Dis = IINF, i->InQ = 0;
(Q[++Tl] = N)->Dis = 0;
while (Hd ^ Tl) {
Node* Cur(Q[++Hd]);
for (auto i:Cur->E) if((i.To->Dis > Cur->Dis + i.Val) && (i.Cap)) {
i.To->Dis = Cur->Dis + i.Val;
if(!(i.To->InQ)) i.To->InQ = 1, Q[++Tl] = i.To;
}
Cur->InQ = 0;
}
return N[n + 2].Dis < IINF;
}
inline unsigned DFS(Node* x, unsigned Come) {
x->InQ = 1;
if(x == N + n + 2) {Ans += x->Dis * Come; return Come;}
unsigned Res(Come);
for (unsigned i(x->E.size() - 1); ~i; --i)
if((x->E[i].Cap) && (x->E[i].To->Dis == x->Dis + x->E[i].Val) && (!(x->E[i].To->InQ))) {
unsigned Go(min(Res, x->E[i].Cap)), Push(DFS(x->E[i].To, Go));
x->E[i].To->InQ = 0;
if(Go ^ Push) x->E[i].To->Dis = IINF;
Res -= Push, x->E[i].Cap -= Push, x->E[i].To->E[x->E[i].Inv].Cap += Push;
if(!Res) break;
}
return Come - Res;
}
signed main() {
n = RD(), m = RD();
for (unsigned i(1); i <= n; ++i) a[i] = RD();
for (Node* i(N + n + 2); i > N; --i) i->E.push_back((Edge){i - 1, 0, 0, 1});
for (Node* i(N + n + 1); i >= N; --i) i->E.push_back((Edge){i + 1, 0, INF - a[i - N], 0});
N[1].E[0].Inv = 0;
for (unsigned i(1); i <= m; ++i) {
A = RD(), B = RD(), C = RD();
Link(N + A, N + B + 1, C);
}
while (SPFA()) DFS(N, INF);
printf("%lld\n", Ans);
return Wild_Donkey;
}
AT2689
无限硬币, 有 n 枚正面朝上, 每次翻转长度为奇数质数的一个区间, 求使硬币都朝下的最少操作数.
我们将原序列需要翻转的区间情况差分, 得到一个含有偶数个 1 的差分数组.
发现奇质数可以凑出任意偶数 (奇质数的差可以凑出 2, 4, 之和可以凑出很可观的正整数范围内的所有偶数), 而一个奇合数可以被 3 和一个偶数凑出, 一共用了 3 个奇质数.
由此发现每次可以将两个 1 同时消去, 而两个 1 坐标之差决定了消去的花费.
-
j−i 是奇质数
花费为 1, 优先考虑, 在差为奇质数的 1 之间连边, 跑二分图最大匹配.
剩下的点之间没有距离为奇质数的了, 所以距离只有奇偶之分, 设剩下点的坐标 a 个奇数, b 个偶数, a+b 是偶数.
我们需要使 a+b2 点对中, 尽可能少的点对距离为奇数.
-
a, b 是偶数
则我们只要将坐标奇偶性相同的点作为一对点, 这样就可以用 a+b 次操作消除所有点了.
-
a, b 是奇数
仍然将奇偶性相同的点放到一对, 发现最后剩下一对点奇偶性不同, 它们花费为 3, 其余点对花费 2, 所以操作数 a+b+1.
unsigned a[205], b[205], m, n;
unsigned A, B, C, D, t;
unsigned Ans(0), Tmp(0);
unsigned Prime[1000005], Cnt(0);
bitset <10000005> IsntP;
struct Node;
struct Edge {
Node* To;
unsigned Inv;
char Cap;
};
struct Node {
vector<Edge> E;
unsigned Dep;
}N[205], * Q[205];
inline void GetPrime () {
for (unsigned i(2); i <= 10000000; ++i) {
if(!(IsntP[i])) Prime[++Cnt] = i;
for (unsigned j(1); Prime[j] * i <= 10000000; ++j) {
IsntP[Prime[j] * i] = 1;
if(!(i % Prime[j])) break;
}
}
}
inline void Link(Node* x, Node* y) {
x->E.push_back((Edge){y, 0, 1});
y->E.push_back((Edge){x, 0, 0});
x->E.back().Inv = y->E.size() - 1;
y->E.back().Inv = x->E.size() - 1;
}
inline char BFS () {
for (Node* i(N + Cnt + 1); i > N; --i) i->Dep = 0x3f3f3f3f;
unsigned Hd(0), Tl(0);
(Q[++Tl] = N)->Dep = 1;
while (Hd ^ Tl) {
Node* Cur(Q[++Hd]);
for (auto i:Cur->E) if((i.Cap) && (i.To->Dep >= 0x3f3f3f3f))
Q[++Tl] = i.To, i.To->Dep = Cur->Dep + 1;
}
return N[1].Dep < 0x3f3f3f3f;
}
inline unsigned DFS(Node* x, unsigned Come) {
if(x == N + 1) {++Ans; return 1;}
unsigned Res(Come);
for (unsigned i(x->E.size() - 1); ~i; --i)
if((x->E[i].Cap) && (x->E[i].To->Dep == x->Dep + 1)) {
char Push(DFS(x->E[i].To, 1));
if(!Push) {x->E[i].To->Dep = 0x3f3f3f3f; continue;}
--Res, --(x->E[i].Cap), ++(x->E[i].To->E[x->E[i].Inv].Cap);
if(!Res) break;
}
return Come - Res;
}
signed main() {
GetPrime();
n = RD(), Cnt = 0, IsntP[0] = IsntP[1] = 1;
for (unsigned i(1); i <= n; ++i) a[i] = RD();
sort(a + 1, a + n + 1);
for (unsigned i(1), j(1); i <= n;) {
while (a[j] + 1 == a[j + 1]) ++j;
b[++Cnt] = a[i], b[++Cnt] = a[j] + 1, i = j + 1, j = i;
}
for (unsigned i(1); i <= Cnt; ++i) {
if(b[i] & 1) {
Link(N, N + i + 1), ++A;
for (unsigned j(1); j <= Cnt; ++j) if(!(b[j] & 1))
if(!IsntP[max(b[j], b[i]) - min(b[j], b[i])]) Link(N + i + 1, N + j + 1);
} else Link(N + i + 1, N + 1), ++B;
}
while (BFS()) DFS(N, 0x3f3f);
A -= Ans, B -= Ans, Ans += A + B + (A & 1), printf("%u\n", Ans);
return Wild_Donkey;
}
AT2645
给 n 个人, 每个人可以坐 (−∞,li]∪[ri,∞) 的椅子, 在 [1, m] 的每个整点都放着一个椅子.
如果希望人人都能坐椅子, 最少需要在任意实数点放多少椅子.
n,m≤2∗105
这个题可以不用管放椅子的问题, 因为既然往实数点放了, 就一定可以想让谁坐, 就找到一个位置放下椅子让他坐, 所以我们只要求原来整点上的椅子和人的最大匹配就可以了.
但是这个题如果用二分图匹配, 每个人连出 O(m) 条边, 则总边数就是 O(nm) 的, 这样跑二分图匹配就是 O(nm√n), 是绝对不行的.
因为建边的特殊性, 考虑前后缀和优化建边, 这样用 3m+n 个点, 4m+2n 条边将图建出来, 然后跑二分图.
下面这份 Dinic 跑二分图, 在 48 个点中过了 31 个.
unsigned a[10005], m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
struct Node;
struct Edge {
Node* To;
unsigned Cap, Inv;
};
struct Node {
vector<Edge> E;
unsigned Dep;
}N[800005], * Q[800005], * Peo, * Suf, * Pre, * Cha(N + 1);
inline void Link(Node* x, Node* y) {
x->E.push_back((Edge){y, INFi, 0});
y->E.push_back((Edge){x, 0, 0});
x->E.back().Inv = y->E.size() - 1;
y->E.back().Inv = x->E.size() - 1;
}
inline char BFS() {
for (Node* i(Peo + n + 1); i > N; --i) i->Dep = 0x3f3f3f3f;
unsigned Hd(0), Tl(0);
(Q[++Tl] = N)->Dep = 1;
while (Hd ^ Tl) {
Node* Cur(Q[++Hd]);
for (auto i:Cur->E) if((i.Cap) && (i.To->Dep >= 0x3f3f3f3f))
i.To->Dep = Cur->Dep + 1, Q[++Tl] = i.To;
}
return N[1].Dep < 0x3f3f3f3f;
}
inline unsigned DFS(Node* x, unsigned Come) {
if(x == N + 1) {--Ans; return 1;}
unsigned Res(Come);
for (unsigned i(x->E.size() - 1); ~i; --i)
if((x->E[i].Cap) && (x->E[i].To->Dep == x->Dep + 1)) {
unsigned Go(min(Res, x->E[i].Cap)), Push(DFS(x->E[i].To, Go));
if(Go ^ Push) x->E[i].To->Dep = 0x3f3f3f3f;
Res -= Push, x->E[i].Cap -= Push, x->E[i].To->E[x->E[i].Inv].Cap += Push;
if(!Res) break;
}
return Come - Res;
}
signed main() {
Ans = n = RD(), Pre = N + (m = RD()) + 1, Suf = Pre + m, Peo = Suf + m;
for (unsigned i(1); i <= m; ++i) {
Cha[i].E.push_back((Edge){N + 1, 1, i - 1});
N[1].E.push_back((Edge){Cha + i, 0, 0});
Cha[i].E.push_back((Edge){Pre + i, 0, 0});
Pre[i].E.push_back((Edge){Cha + i, 1, 1});
Cha[i].E.push_back((Edge){Suf + i, 0, 0});
Suf[i].E.push_back((Edge){Cha + i, 1, 2});
}
for (unsigned i(1); i <= n; ++i) {
Peo[i].E.push_back((Edge){N, 0, i - 1});
N->E.push_back((Edge){Peo + i, 1, 0});
}
for (unsigned i(2); i <= m; ++i) Link(Pre + i, Pre + i - 1);
for (unsigned i(1); i < m; ++i) Link(Suf + i, Suf + i + 1);
for (unsigned i(1); i <= n; ++i) {
A = RD(), B = RD();
if(A) Link(Peo + i, Pre + A);
if(B <= m) Link(Peo + i, Suf + B);
}
while (BFS()) DFS(N, INFi);
printf("%u\n", Ans);
return Wild_Donkey;
}
但是我怎么能只会写 Dinic 呢, ISAP 赶紧安排上, 结果发现只过了 24 个点.
unsigned m, n, m3n1;
unsigned Gap[800005];
inline void BFS() {
for (Node* i(Peo + n); i >= N; --i) i->Dep = 0x3f3f3f3f;
unsigned Hd(0), Tl(0);
++Gap[(Q[++Tl] = N + 1)->Dep = 0];
while (Hd ^ Tl) {
Node* Cur(Q[++Hd]);
for (auto i:Cur->E) if((i.To->E[i.Inv].Cap) && (i.To->Dep >= 0x3f3f3f3f))
++Gap[i.To->Dep = Cur->Dep + 1], Q[++Tl] = i.To;
}
}
inline unsigned DFS(Node* x, unsigned Come) {
if(x == N + 1) {--Ans; return 1;}
unsigned Res(Come);
for (unsigned i(x->E.size() - 1); ~i; --i)
if((x->E[i].Cap) && (x->E[i].To->Dep + 1 == x->Dep)) {
unsigned Go(min(Res, x->E[i].Cap)), Push(DFS(x->E[i].To, Go));
Res -= Push, x->E[i].Cap -= Push, x->E[i].To->E[x->E[i].Inv].Cap += Push;
if(!Res) return Come;
}
if(!(--Gap[(x->Dep)++])) N->Dep = m3n1 + 1;
++Gap[x->Dep];
return Come - Res;
}
signed main() {
Ans = n = RD(), Pre = N + (m = RD()) + 1, Suf = Pre + m, Peo = Suf + m;
m3n1 = (m << 1) + m + n;
/*建边, 同上*/
BFS();
while (N->Dep <= m3n1) DFS(N, INFi);
printf("%u\n", Ans);
return Wild_Donkey;
}
在当前弧优化 (不放代码了, 这文章太 TM 长了) 之后, 少 T 了几个点, 但还是没跑过 Dinic.
所以查看正解, 需要用到 Hall 定理的一个推论, 如果 S 表示左部点的一个子集, R(S) 表示它们能连接的右部点的点集, 那么 n−max(|S|−|R(S)|) 就是二分图的最大匹配.
因为我们要求 n−最大匹配, 所以就是求 max(|S|−|R(S)|).
结合此题连边方式的特殊性, R(S) 事实上是 S 中的所有连边区间的并, 我们知道, 一些区间的并, 就是这些区间的补的交的补, 这样比较好做.
转化为求 S, 使得 |S| 加上它所有连边补区间的交最大, 答案就是这个值减去 m.
因为显然这个交一定是一段区间, 所以我们可以用枚举区间的惯用伎俩, 枚举右端点, 线段树扫描左端点.
当交确定的时候, 这是需要让 S 最大. 那么一定是把所有连边补区间包含这个区间的都算上, 我们需要查询所有右端点 ≥R, 并且左端点 ≤L 的区间数量, 可以按右端点排序, 然后从大到小加入线段树, 查询 [1,L] 区间数量即可.
优化方面, 需要快速查询 L∈[1,R] 的 [1,L] 区间和加上 R−L+1 的最大值, 所以首先需要给每个位置都减去 L, 然后每次查询之后全局加 R+1.
所以我们要求的是线段树上点的前缀和减去 L 的最大值, 可以认为减 L 是序列 −1,−1,...,−1,−1 的前缀和.
所以不如直接维护前缀和, 把单点修改变成区间修改, 然后查询区间最值即可.
对于 −L, 建树时维护即可.
具体实现仍有不同, 因为实在不想用有符号整型, 所以给线段树每个点赋初值 m−L, 最后多减一个 m 即可.
线段树方面因为是后缀修改和前缀查询, 优化了一些冗余判断.
统计答案时因为永远都要减 m, 所以放到最后一起统计, 这样临时答案就累计了 m<<1 的偏移. 因为交区间为空的情况不好询问, 所以提前将这种情况的答案统计上 (max(n−m,0), 偏移后是 max(n+m,m<<1)), 输出时不要忘记修正 m<<1 的偏移.
从图论绕到我的主场数据结构, 真是如回家般亲切啊.
pair<unsigned, unsigned> a[200005];
unsigned m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
struct Node {
Node* LS, * RS;
unsigned Val, Tag;
inline void PsDw() {
if(Tag) {
LS->Tag += Tag;
RS->Tag += Tag;
LS->Val += Tag;
RS->Val += Tag;
Tag = 0;
}
}
inline void Change(unsigned L, unsigned R) {
if(A <= L) {++Val, ++Tag; return;}
unsigned Mid((L + R) >> 1);
PsDw();
if(A <= Mid) LS->Change(L, Mid);
RS->Change(Mid + 1, R);
Val = max(LS->Val, RS->Val);
}
inline void Qry(unsigned L, unsigned R) {
if(R <= A) {C = max(Val, C); return;}
unsigned Mid((L + R) >> 1);
PsDw();
LS->Qry(L, Mid);
if(A > Mid) RS->Qry(Mid + 1, R);
}
}N[400005], * CntN(N);
inline void Build (Node* x, unsigned L, unsigned R) {
if(L == R) {x->Val = m - L; return;}
unsigned Mid((L + R) >> 1);
Build(x->LS = ++CntN, L, Mid);
Build(x->RS = ++CntN, Mid + 1, R);
x->Val = max(x->LS->Val, x->RS->Val);
}
signed main() {
n = RD(), m = RD(), Build(N, LE, RE);
Ans = max(n + m, m << 1);
for (unsigned i(1); i <= n; ++i) a[i].second = RD() + 1, a[i].first = RD() - 1;
sort(a + 1, a + n + 1);
for (unsigned i(n); i; --i) {
if(a[i].second <= m) A = a[i].second, N->Change(LE, RE);
if(a[i].first ^ a[i - 1].first) {
A = a[i].first, C = 0, N->Qry(LE, RE);
Ans = max(Ans, C + a[i].first + 1);
}
}
printf("%u\n", Ans - (m << 1));
return Wild_Donkey;
}
CF1288F
一个二分图, 有三种节点, R, B, U, 尝试给边染色使得 R 点连接的 R 边严格大于 B 边, B 点 连接的 B 边严格大于 R 边.
每条 R 边花费 r 的代价, B 边花费 b 的代价, 求满足条件的花费最小的染色方案并且求这个最小花费.
考虑最小费用最大流, 一个点从对面的点流入的流量和流向对面的点的流量表示它相邻的边染成不同的颜色, 一个点从源点流入的流量或流向汇点的流量表示它自己需要满足某种颜色严格大于另一种的限制, 这样在保证每个点流量平衡的前提下, 流入和流出的流量相等, 其中从源点流入的流量或者从汇点流出的流量就是自己同色的边比另一种颜色多出来的边数.
从源点向左部的 R 和右部的 B 连倒贴钱的流量为 1 的边, 表示至少应该多染一条 R/B.
从左部的 B 和右部的 G 向汇点连倒贴钱的流量为 1 的边, 表示至少应该多染一条 B/R.
规定左部 R 从右部点的流入流量代表染 B, 流出到右部点的流量代表染 G, 从源点流入的流量只要非负, 在流量平衡的前提下, 这个 R 点相邻的 R 边就一定比 B 边多.
其它点也是类似地保证方案的合法性, 左部点都是流入 B, 流出 R, 右部点都是流入 R 流出 B, 所以我们只要对于每条二分图上的边, 连一条从左往右的花费 r , 流量 1 的边表示这条边选 R 的情况, 连一条花费 b, 流量 1 的边表示这条边选 B 的情况.
但是一个点染的同色边不仅仅可以比异色边多一条, 也可以多 >1 条, 但是这个数量不会使得答案更优, 所以我们不在边权上进行诱导, 所以每条倒贴钱的边, 复制出一条免费的流量不限的边即可.
对于 U 点, 它们无论左右都和源汇连边, 表示它连接的 R 边 B 边谁多谁少无所谓, 所以也是都连免费的流量无限边.
图建完了, 接下来考虑流的意义, 一条流从源点流出, 经过一条边到达一个点. 如果这条边倒贴钱, 表示满足了一个点的限制, 然后通往另一个点, 花费这个点流出边对应的颜色的花费.
对于新的点, 如果这个流经过一条边通往汇点, 且倒贴钱, 说明又满足了一个点的限制, 如果这条边是免费的, 说明这个点的限制已经被满足了.
如果流经过这个点后没有通往汇点, 则相当于流入又流出, 给这个点的同时染了两种不同颜色的边, 花费了入边出边两条边的代价, 然后在新到达的点重复上面的过程.
如果一股流一条倒贴钱的边都没有经过, 那么它不会对局面的合法性造成任何影响, 因为没有一个点的限制被它所满足, 所以这股流只能使得答案更劣, 无需计算.
所以我们跑 EK + SPFA, 每次增广 (S,T) 的最短路, 当最短路非负的时候结束算法.
判断一个局面是否合法也很简单, 因为每个有色点的限制都被满足当且仅当所有的倒贴钱的边都被经过, 所以我们只要计算有多少边倒贴钱了即可.
unsigned a[10005], m1, n1, n2, r, b;
unsigned A, B, C, D, t, Tl(0), Hd(0);
unsigned Cnt(0), Ans(0), Tmp(0);
unsigned Pr[205][2][2];
char IO[205];
struct Node;
struct Edge {
Node* To;
unsigned Inv, Cap;
int Val;
};
struct Node {
vector<Edge> E;
Node* Pre;
unsigned Come;
int Dis;
}N[405], * Q[100005], *N1(N + 1), * N2;
inline void Link(Node* x, Node* y, const unsigned Ca, const int Va) {
x->E.push_back((Edge){y, 0, Ca, Va});
y->E.push_back((Edge){x, 0, 0, -Va});
x->E.back().Inv = y->E.size() - 1;
y->E.back().Inv = x->E.size() - 1;
}
inline char SPFA() {
for (Node* i(N2 + n2); i > N; --i) i->Dis = INF;
Hd = Tl = 0;
(Q[++Tl] = N)->Dis = 0;
while (Hd ^ Tl) {
Node* Cur(Q[++Hd]);
for (unsigned i(Cur->E.size() - 1); ~i; --i)
if((Cur->E[i].Cap) && (Cur->E[i].To->Dis > Cur->Dis + Cur->E[i].Val)) {
Cur->E[i].To->Pre = Cur, Cur->E[i].To->Come = i;
Cur->E[i].To->Dis = Cur->Dis + Cur->E[i].Val, Q[++Tl] = Cur->E[i].To;
}
}
return N[1].Dis < 0;
}
signed main() {
N2 = N1 + (n1 = RD()), n2 = RD(), m1 = RD(), r = RD(), b = RD();
scanf("%s", IO + 1);
for (unsigned i(1); i <= n1; ++i) {
if(IO[i] == 'R') Link(N, N1 + i, 1, -INF), Link(N, N1 + i, 400, 0), ++Cnt;
if(IO[i] == 'B') Link(N1 + i, N + 1, 1, -INF), Link(N1 + i, N + 1, 400, 0), ++Cnt;
if(IO[i] == 'U') Link(N, N1 + i, 400, 0), Link(N1 + i, N + 1, 400, 0);
}
scanf("%s", IO + 1);
for (unsigned i(1); i <= n2; ++i) {
if(IO[i] == 'R') Link(N2 + i, N + 1, 1, -INF), Link(N2 + i, N + 1, 400, 0), ++Cnt;
if(IO[i] == 'B') Link(N, N2 + i, 1, -INF), Link(N, N2 + i, 400, 0), ++Cnt;
if(IO[i] == 'U') Link(N, N2 + i, 400, 0), Link(N2 + i, N + 1, 400, 0);
}
for (unsigned i(1); i <= m1; ++i) {
A = RD(), B = RD();
Link(N1 + A, N2 + B, 1, r), Pr[i][0][0] = A, Pr[i][0][1] = N1[A].E.size() - 1;
Link(N2 + B, N1 + A, 1, b), Pr[i][1][0] = B, Pr[i][1][1] = N2[B].E.size() - 1;
}
while (SPFA()) {
Node* Cur(N + 1);
unsigned Flow(INF);
while (Cur > N) Flow = min(Flow, Cur->Pre->E[Cur->Come].Cap), Cur = Cur->Pre;
Ans += Flow * (Cur = N + 1)->Dis;
while (Cur > N) Cur->Pre->E[Cur->Come].Cap -= Flow, Cur->E[Cur->Pre->E[Cur->Come].Inv].Cap += Flow, Cur = Cur->Pre;
}
Ans += Cnt * INF;
if(Ans >= INF) {printf("-1\n");return 0;}
printf("%d\n", Ans);
for (unsigned i(1); i <= m1; ++i) {
if(!(N1[Pr[i][0][0]].E[Pr[i][0][1]].Cap)) putchar('R');
else if(!(N2[Pr[i][1][0]].E[Pr[i][1][1]].Cap)) putchar('B');
else putchar('U');
}
return Wild_Donkey;
}
Day18: 模拟赛
期望 360 炸成 210, 真不是我假, 考完试就说我挂了 TMD 100+.
A
一个 ST 题, 放在 T1 还算合理.
但是...
样例诈骗不讲武德, ST 表写炸了样例全过, 结果爆 0.
unsigned Lst[2000005], a[2][1000005][20], Pos[1000005][2][2], Bin[1000005], Log[1000005], m, n, Cnt(0), Ans(0);
inline unsigned Find(unsigned L, unsigned x, unsigned y) {
register unsigned Tmp(Log[y - x + 1]);
return max(a[L][x][Tmp], a[L][y - Bin[Tmp] + 1][Tmp]);
}
int main() {
n = RD();
for (register unsigned b(0); b < 2; ++b) {
for (register unsigned i(1); i <= n; ++i) {
Lst[++Cnt] = a[b][i][0] = RD();
}
}
sort(Lst + 1, Lst + Cnt + 1);
unique(Lst + 1, Lst + Cnt + 1);
for (register unsigned b(0); b < 2; ++b) {
for (register unsigned i(1); i <= n; ++i) {
a[b][i][0] = lower_bound(Lst + 1, Lst + n + 1, a[b][i][0]) - Lst;
if(Pos[a[b][i][0]][0][1]) {
Pos[a[b][i][0]][1][0] = b;
Pos[a[b][i][0]][1][1] = i;
} else {
Pos[a[b][i][0]][0][0] = b;
Pos[a[b][i][0]][0][1] = i;
}
}
}
for (register unsigned i(1), j(0); i <= n; i <<= 1, ++j) {
Bin[j] = i, Log[i] = j;
}
for (register unsigned i(2); i <= n; ++i) {
Log[i] = max(Log[i], Log[i - 1]);
}
for (register unsigned b(0); b < 2; ++b) {
for (register unsigned i(1); i <= Log[n]; ++i) {
for (register unsigned j(1); j + Bin[i] <= n + 1; ++j) {
a[b][j][i] = max(a[b][j][i - 1], a[b][j + Bin[i - 1]][i - 1]);
}
}
}
for (register unsigned i(n); i; --i) {
if(Pos[i][0][0] ^ Pos[i][1][0]) {
Ans = max(Ans, i);
continue;
}
if(Pos[i][0][1] > Pos[i][1][1]) {
swap(Pos[i][0][1], Pos[i][1][1]);
}
if(Pos[i][0][1] + 1 == Pos[i][1][1]) {
continue;
}
Ans = max(min(i, Find(Pos[i][0][0], Pos[i][0][1] + 1, Pos[i][1][1] - 1)), Ans);
}
printf("%u\n", Lst[Ans]);
return Wild_Donkey;
}
B
求一个数 x 和序列中所有数的差的平方和.
这个答案对 x 成二次函数关系, 所以只要用所有数的平方和和总和求出解析式然后 O(1) 求答案即可.
大水题, 本来可以 O(n), 但是数据非要开 3000.
所以我们 O(n) 枚举这个数即可, 总复杂度 O(n2).
unsigned a[10005], m, n, Cnt(0), Sum(0);
unsigned long long Ans(0x3f3f3f3f3f3f3f3f), Tmp, A;
char b[10005];
inline void Clr() {}
int main() {
n = RD();
for (register unsigned i(1); i <= n; ++i) {
Sum += (a[i] = RDsg() + 4000);
}
Sum /= n;
for (register unsigned i(1000); i <= 7000; ++i) {
Tmp = 0;
for (register unsigned j(1); j <= n; ++j) {
A = max(a[j], i) - min(a[j], i);
Tmp += A * A;
}
Ans = min(Ans, Tmp);
}
printf("%llu\n", Ans);
return Wild_Donkey;
}
C
我到 AC 都不知道暴力怎么写./kk
线段树 + 二分答案事实上可以优化成 ST + 二分答案, 这样就能将 O(nlog2n) 优化到 O(nlogn).
然后我就看着老师三年前的代码拿着 O(n3) 的复杂度跑得比我 O(nlogn) 都快.
26 个字母的出现情况状态压缩成一个整数, 线段树查询区间的出现情况, O(26) 找出出现字母数量, 然后直接 DP 即可.
unsigned f[200005][20], b[200005], Bin[205], Log[200005], m, n, Cnt[30], BinL, BinR, BinMid, A, B, C, D, t, Ans(0), Tmp(0), NowL, NowR, LastL, LastR;
char ap[200005], *a(ap);
struct Node {
Node *LS, *RS;
unsigned Val;
}N[500005], *CntN(N);
void Build(Node *x, unsigned L, unsigned R) {
if(L == R) {
x->Val = b[L];
return;
}
register unsigned Mid((L + R) >> 1);
Build(x->LS = ++CntN, L, Mid);
Build(x->RS = ++CntN, Mid + 1, R);
x->Val = (x->LS->Val) | (x->RS->Val);
return;
}
inline unsigned Count (unsigned x) {
register unsigned Ctmp(0);
for (register char i(0); i < 26; ++i) {
Ctmp += (x & (1 << i)) ? 1 : 0;
}
return Ctmp;
}
void Qry(Node *x, unsigned L, unsigned R) {
if((A <= L) && (R <= B)) {
C |= x->Val;
return;
}
register unsigned Mid((L + R) >> 1);
if(B > Mid) {
Qry(x->RS, Mid + 1, R);
}
if(A <= Mid) {
Qry(x->LS, L, Mid);
}
return;
}
char Judge1 (unsigned x) {
A = x, B = D, C = 0, Qry(N, 1, n);
return Count(C) <= m;
}
char Judge2 (unsigned x) {
A = x, B = D, C = 0, Qry(N, 1, n);
return Count(C) >= m;
}
inline unsigned Find(unsigned x, unsigned y) {
register unsigned Tmp(Log[y - x + 1]);
return min(f[x][Tmp], f[y - Bin[Tmp] + 1][Tmp]);
}
int main() {
m = RD();
fread(ap + 1, 1, 200002, stdin);
while (a[1] < 'a') ++a;
while (a[n + 1] >= 'a') ++n;
for (register unsigned i(1); i <= n; ++i) {
b[i] = 1 << (a[i] - 'a');
}
Build(N, 1, n);
for (register unsigned i(1), j(0); i <= n; i <<= 1, ++j) {
Bin[j] = i, Log[i] = j;
}
for (register unsigned i(1); i <= n; ++i) {
Log[i] = max(Log[i], Log[i - 1]);
}
NowL = NowR = 0;
for (register unsigned i(1); i <= n; ++i) {
D = i, BinL = 1, BinR = i;
while (BinL ^ BinR) {
BinMid = (BinL + BinR) >> 1;
if(Judge1(BinMid)) {
BinR = BinMid;
} else {
BinL = BinMid + 1;
}
}
NowL = BinL;
BinL = 0, BinR = i;
while (BinL ^ BinR) {
BinMid = (BinL + BinR + 1) >> 1;
if(Judge2(BinMid)) {
BinL = BinMid;
} else {
BinR = BinMid - 1;
}
}
NowR = BinL;
f[0][0] = 0;
if(NowR <= 0) {
f[i][0] = 0x3f3f3f3f;
} else {
if(!NowL) NowL = 1;
f[i][0] = Find(NowL - 1, NowR - 1) + 1;
}
for (register unsigned j(1); j <= Log[i]; ++j) {
f[i - Bin[j] + 1][j] = min(f[i - Bin[j - 1] + 1][j - 1], f[i - Bin[j] + 1][j - 1]);
}
if(f[i][0] >= 0x3f3f3f3f) {
printf("-1\n");
} else {
printf("%u\n", f[i][0]);
}
}
return Wild_Donkey;
}
发现二分得到的 l, r 单调递增, 所以直接双指针扫描即可, 可以被进一步优化掉, 但是由于查询时仍然需要动态 ST 表, 所以仍然是 O(nlogn).
D
O(nm2m) 暴力给了 50′, 据说 10min 码量, 我没写.
转化为在一个 m 维超空间内的 n 个点中找出每维坐标为 0 或 1 的点使得它到最近的点的曼哈顿距离最小.
既然是找最短曼哈顿距离, 考虑多源 BFS (我竟然没想到, 在我喊出这 5 个字符后一秒钟老师就喊出了这个 5 个字符).
unsigned Now(0), Ways(0), Q[1500005], Dist[1500005], Hd(0), Tl(0), m, N, n, Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
char Faq[104];
int main() {
n = RD() - 1, m = RD(), N = (1 << m);
memset(Dist, 0x3f, ((N + 1) << 2));
for (register unsigned i(1), Tmpi(0); i <= n; ++i) {
scanf("%s", Faq);
Tmpi = 0;
for (register unsigned j(0); j < m; ++j) {
Tmpi <<= 1, Tmpi += Faq[j] - '0';
}
Dist[Q[++Tl] = Tmpi] = 0;
}
while (Hd < Tl) {
Now = Q[++Hd];
for (register unsigned i(0), Nowi(0); i < m; ++i) {
Nowi = Now ^ (1 << i);
if(Dist[Nowi] >= 0x3f3f3f3f) {
Dist[Nowi] = Dist[Now] + 1;
Q[++Tl] = Nowi;
if(Dist[Nowi] > Ans) {
Ans = Dist[Nowi];
Ways = 1;
} else {
++Ways;
}
}
}
}
printf("%u %u\n", m - Ans, Ways);
return Wild_Donkey;
}
E
写的 O(n3m4n) 暴力, 期望 60′, 但是发现 60′ 的极限数据 8 64 本地跑了 2s, 所以用打表来卡常. (以表代卡的操作我自己都佩服我能这么不要脸)
实际 10′, 原因是代码中有一个 j 写成了 i.
这就是 60′ 代码:
const unsigned long long _1(1);
const unsigned long long MOD(998244353);
unsigned f[70005], m, n, N, Cnt(0), A, B, C, D, t, Ans(0);
unsigned long long Tmp(0), List[100005];
inline void Print(unsigned long long x) {
for (register unsigned i(0); i < (n << 1); ++i){
putchar(((_1 << i) & x) ? '1' : '0');
}
putchar('\n');
return;
}
inline unsigned long long To(unsigned long long x, unsigned long long y) {
register unsigned long long L;
while (x) {
L = Lowbit(x);
if(y & L) {
y ^= (L | (L << 1));
} else {
y ^= L;
}
x ^= L;
}
return y;
}
unsigned Ans8[70] = {0, 93, 8649, 804357, 69214125, 112083636, 213453520, 809812580, 188050035, 477063355, 850898529, 35219241, 307515998, 706132945, 927739308, 824492602, 209069661, 455485934, 83153968, 899084763, 24004137, 91973932, 371377882, 867221422, 958079829, 625859287, 415129069, 705640832, 593093251, 673002824, 528839686, 497928375, 357631902, 563997465, 840065963, 499164109, 730913293, 70374125, 541521928, 361751373, 572725556, 743972069, 598729144, 137289737, 980579798, 284153995, 397542183, 985374208, 811482227, 357658360, 596769980, 373919314, 712588041, 897470897, 602075230, 668019421, 580949849, 425155212, 577434159, 871327693, 174840186, 382383295, 282033847, 847049313, 742770833};
int main() {
n = RD(), m = RD();
if(n > m) swap(n, m);
if(n == 8) {
printf("%u\n", Ans8[m]);
return 0;
}
for (register unsigned i(0); i < n; ++i) {
List[++Cnt] = (_1 << i);
}
for (register unsigned i(0); i < n; ++i) {
for (register unsigned j(i + 1); j < n; ++j) {
List[++Cnt] = (_1 << i) | (_1 << j);
}
}
for (register unsigned i(0); i < n; ++i) {
for (register unsigned j(i + 1); j < n; ++j) {
for (register unsigned k(j + 1); k < n; ++k) {
List[++Cnt] = (_1 << i) | (_1 << j) | (_1 << k);
}
}
}
for (register unsigned i(1); i <= Cnt; ++i) {
for (register unsigned j(n - 1); j; --j) {
if((_1 << j) & List[i]) {
List[i] ^= (_1 << j);
List[i] ^= (_1 << (j << 1));
}
}
}
N = 1 << (n << 1);
f[0] = 1;
for (register unsigned i(1); i <= m; ++i) {
for (register unsigned long long k(N - 1); k < 0x3f3f3f3f3f3f3f3f; --k) {
for (register unsigned j(1); j <= Cnt; ++j) {
if((List[j] & k) & (((List[j] << 1) & k) >> 1)) {
continue;
}
Tmp = To(List[j], k);
f[Tmp] += f[k];
if(f[Tmp] >= MOD) f[Tmp] -= MOD;
}
}
}
for (register unsigned i(0); i < N; ++i) {
Ans += f[i];
if(Ans >= MOD) Ans -= MOD;
}
printf("%u\n", Ans);
return Wild_Donkey;
}
然后是正解: 发现每一列的位置不一定要特别讨论, 只要知道当前状态有多少列有 0 个 1, 多少列有 1 个 1, 多少列有 2 个 1, 多少列有 3 个 1 即可, 因为列数是 n 所以这 4 个量知 3 推 1.
设计状态 fi,j,k,l 表示讨论到第 i 列, 有 j 列没有 1, k 列有 1 一个 1, l 有 2 个 1.
转移也比较简单, 只要枚举本层的 1 有几个放在 j 表示的列中, 几个放在 k 表示的列中, 几个在 l 表示的列中, 用排列组合求出不同的情况数, 总共有大约 20 种分配方式.
这就是 100′ 的代码.
const unsigned long long Mod(998244353);
unsigned long long f[65][68][68][68];
unsigned long long C1[68], C2[68], C3[68], Ans(0);
unsigned m, n, Cnt(0), A, B, C, D, t;
int main() {
n = RD(), m = RD(), f[0][0][0][0] = 1;
for (unsigned i(1); i <= n; ++i)
C1[i] = i, C2[i] = (C1[i] * (C1[i] - 1)) >> 1, C3[i] = (C2[i] * (C1[i] - 2)) / 3;
C3[2] = C3[1] = C2[1] = 0;
for (unsigned i(1); i <= m; ++i) {
for (unsigned j1(n); ~j1; --j1) {
for (unsigned j2(n - j1); ~j2; --j2) {
for (unsigned j3(n - j1 - j2); ~j3; --j3) {
f[i][j1][j2][j3] += f[i - 1][j1][j2][j3]; if(f[i][j2][j3][j3] >= Mod) f[i][j1][j2][j3] -= Mod;
if(j1) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1 - 1][j2 + 1][j3] * C1[j2 + 1]) % Mod;
if(j2) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1][j2 - 1][j3 + 1] * C1[j3 + 1]) % Mod;
if(j3) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1][j2][j3 - 1] * C1[n - j1 - j2 - j3 + 1]) % Mod;
if(j1 > 1) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1 - 2][j2 + 2][j3] * C2[j2 + 2]) % Mod;
if(j2 > 1) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1][j2 - 2][j3 + 2] * C2[j3 + 2]) % Mod;
if(j3 > 1) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1][j2][j3 - 2] * C2[n - j1 - j2 - j3 + 2]) % Mod;
if(j1) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1 - 1][j2][j3 + 1] * C1[j2] * C1[j3 + 1]) % Mod;
if(j1 && j3) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1 - 1][j2 + 1][j3 - 1] * C1[j2 + 1] * C1[n - j1 - j2 - j3 + 1]) % Mod;
if(j2) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1][j2 - 1][j3] * C1[j3] * C1[n - j1 - j2 - j3 + 1]) % Mod;
if(j1 > 2) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1 - 3][j2 + 3][j3] * C3[j2 + 3]) % Mod;
if(j2 > 2) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1][j2 - 3][j3 + 3] * C3[j3 + 3]) % Mod;
if(j3 > 2) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1][j2][j3 - 3] * C3[n - j1 - j2 - j3 + 3]) % Mod;
if(j1 > 1) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1 - 2][j2 + 1][j3 + 1] * C2[j2 + 1] * C1[j3 + 1]) % Mod;
if((j1 > 1) && j3) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1 - 2][j2 + 2][j3 - 1] * C2[j2 + 2] * C1[n - j1 - j2 - j3 + 1]) % Mod;
if(j1 && j2) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1 - 1][j2 - 1][j3 + 2] * C2[j3 + 2] * C1[j2 - 1]) % Mod;
if(j2 > 1) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1][j2 - 2][j3 + 1] * C2[j3 + 1] * C1[n - j1 - j2 - j3 + 1]) % Mod;
if(j1 && (j3 > 1)) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1 - 1][j2 + 1][j3 - 2] * C2[n - j1 - j2 - j3 + 2] * C1[j2 + 1]) % Mod;
if(j2 && j3) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1][j2 - 1][j3 - 1] * C2[n - j1 - j2 - j3 + 2] * C1[j3 - 1]) % Mod;
if(j1) f[i][j1][j2][j3] = (f[i][j1][j2][j3] + f[i - 1][j1 - 1][j2][j3] * C1[n - j1 - j2 - j3 + 1] * C1[j3] * C1[j2]) % Mod;
}
}
}
}
for (unsigned i1(n); ~i1; --i1)
for (unsigned i2(n - i1); ~i2; --i2)
for (unsigned i3(n - i1 - i2); ~i3; --i3)
{Ans += f[m][i1][i2][i3]; if(Ans >= Mod) Ans -= Mod;}
printf("%u\n", Ans);
return Wild_Donkey;
}
另可以用滚动数组滚掉第一维, 这样空间复杂度就是 O(n3), 时间复杂度是巨大常数的 O(n4).
更高效的版本:
const unsigned long long Mod(998244353);
unsigned long long f[68][68][68], g[68][68][68];
unsigned long long C1[68], C2[68], C3[68], Ans(0);
unsigned m, n, Cnt(0), A, B, C, D, t;
int main() {
n = RD(), m = RD(), f[0][0][0] = 1;
for (unsigned i(1); i <= n; ++i)
C1[i] = i, C2[i] = (C1[i] * (C1[i] - 1)) >> 1, C3[i] = (C2[i] * (C1[i] - 2)) / 3;
C3[2] = C3[1] = C2[1] = 0;
for (unsigned i(1); i <= m; ++i) {
memcpy(g, f, sizeof(f));
for (unsigned j1(n); ~j1; --j1) for (unsigned j2(n - j1); ~j2; --j2)
for (unsigned j3(n - j1 - j2); ~j3; --j3) {
unsigned long long* k(f[j1][j2] + j3);
*k = g[j1][j2][j3];
if(j1) {
*k = (*k + g[j1 - 1][j2 + 1][j3] * C1[j2 + 1]) % Mod;
*k = (*k + g[j1 - 1][j2][j3 + 1] * C1[j2] * C1[j3 + 1]) % Mod;
*k = (*k + g[j1 - 1][j2][j3] * C1[n - j1 - j2 - j3 + 1] * C1[j3] * C1[j2]) % Mod;
if(j1 > 1) {
*k = (*k + g[j1 - 2][j2 + 2][j3] * C2[j2 + 2]) % Mod;
*k = (*k + g[j1 - 2][j2 + 1][j3 + 1] * C2[j2 + 1] * C1[j3 + 1]) % Mod;
if(j1 > 2) *k = (*k + g[j1 - 3][j2 + 3][j3] * C3[j2 + 3]) % Mod;
}
}
if(j2) {
*k = (*k + g[j1][j2 - 1][j3 + 1] * C1[j3 + 1]) % Mod;
*k = (*k + g[j1][j2 - 1][j3] * C1[j3] * C1[n - j1 - j2 - j3 + 1]) % Mod;
if(j2 > 1) {
*k = (*k + g[j1][j2 - 2][j3 + 2] * C2[j3 + 2]) % Mod;
*k = (*k + g[j1][j2 - 2][j3 + 1] * C2[j3 + 1] * C1[n - j1 - j2 - j3 + 1]) % Mod;
if(j2 > 2) *k = (*k + g[j1][j2 - 3][j3 + 3] * C3[j3 + 3]) % Mod;
}
if(j1) *k = (*k + g[j1 - 1][j2 - 1][j3 + 2] * C2[j3 + 2] * C1[j2 - 1]) % Mod;
if(j3) *k = (*k + g[j1][j2 - 1][j3 - 1] * C2[n - j1 - j2 - j3 + 2] * C1[j3 - 1]) % Mod;
}
if(j3) {
*k = (*k + g[j1][j2][j3 - 1] * C1[n - j1 - j2 - j3 + 1]) % Mod;
if(j3 > 1) {
*k = (*k + g[j1][j2][j3 - 2] * C2[n - j1 - j2 - j3 + 2]) % Mod;
if(j3 > 2) *k = (*k + g[j1][j2][j3 - 3] * C3[n - j1 - j2 - j3 + 3]) % Mod;
if(j1) *k = (*k + g[j1 - 1][j2 + 1][j3 - 2] * C2[n - j1 - j2 - j3 + 2] * C1[j2 + 1]) % Mod;
}
if(j1) {
*k = (*k + g[j1 - 1][j2 + 1][j3 - 1] * C1[j2 + 1] * C1[n - j1 - j2 - j3 + 1]) % Mod;
if(j1 > 1) *k = (*k + g[j1 - 2][j2 + 2][j3 - 1] * C2[j2 + 2] * C1[n - j1 - j2 - j3 + 1]) % Mod;
}
}
}
}
for (unsigned i1(n); ~i1; --i1)
for (unsigned i2(n - i1); ~i2; --i2)
for (unsigned i3(n - i1 - i2); ~i3; --i3)
{Ans += f[i1][i2][i3]; if(Ans >= Mod) Ans -= Mod;}
printf("%u\n", Ans);
return Wild_Donkey;
}
总结
这次考场代码离 360′ 只差 5 个字符, 有 4 个是 T1 的 +1 和 -1, 还有一个是 T5 把 i 改成 j.
悔恨的泪水, 流了下来. (所以为什么样例这么菜啊???)
Day19: 模拟赛
A
无向图, 求点 1 到点 n 的, 强制经过某个点或某条边的最短路.
分别从 1 和 n 跑单源最短路, 然后 O(1) 回答询问.
对于强制走点 i, 答案就是 1 到 i 的最短路加 n 到 i 的最短路.
对于强制走边 i, 它的两个端点为 u,.v, 则讨论经过这条边的方向, 取 min(Dis(1,u)+Dis(n,v),Dis(1,v)+Disn,u)+Vali 作为答案.
unsigned Pnts[200005][2], m, n, Cnt(0), C, D, t, Ans(0), Tmp(0);
char b[10005];
struct Edge;
struct Node {
Edge *Fst;
unsigned long long Dist1, Dist2;
bool InQue;
}N[100005], *A, *B;
struct Edge {
Node *To;
Edge *Nxt;
unsigned long long Val;
}E[400005], *CntE(E);
struct Pnt{
Node *P;
unsigned long long Dist;
const inline char operator <(const Pnt &x) const{
return this->Dist > x.Dist;
}
}TmpP;
void Link (Node *x, Node *y) {
(++CntE)->Nxt = x->Fst;
x->Fst = CntE;
CntE->To = y;
CntE->Val = C;
}
priority_queue<Pnt> Q;
int main() {
n = RD(), m = RD();
for (register unsigned i(1); i <= m; ++i) {
A = N + RD(), B = N + RD(), C = RD();
Link(A, B), Link(B, A);
Pnts[i][0] = A - N, Pnts[i][1] = B - N;
}
for (register unsigned i(1); i <= n; ++i) {
N[i].Dist1 = N[i].Dist2 = 2147483647;
}
TmpP.P, N[1].Dist1 = 0, TmpP.P = N + 1, Q.push(TmpP);
while (Q.size()) {
register Node *Now((Q.top()).P); Q.pop();
if(Now->InQue) continue;
Now->InQue = 1;
Edge *Sid(Now->Fst);
while (Sid) {
if(Sid->To->Dist1 > Now->Dist1 + Sid->Val) {
Sid->To->Dist1 = Now->Dist1 + Sid->Val;
TmpP.Dist = Sid->To->Dist1, TmpP.P = Sid->To, Q.push(TmpP);
}
Sid = Sid->Nxt;
}
}
for (register unsigned i(1); i <= n; ++i) {
N[i].InQue = 0;
}
TmpP.P, N[n].Dist2 = 0, TmpP.P = N + n, Q.push(TmpP);
while (Q.size()) {
register Node *Now((Q.top()).P); Q.pop();
if(Now->InQue) continue;
Now->InQue = 1;
Edge *Sid(Now->Fst);
while (Sid) {
if(Sid->To->Dist2 > Now->Dist2 + Sid->Val) {
Sid->To->Dist2 = Now->Dist2 + Sid->Val;
TmpP.Dist = Sid->To->Dist2, TmpP.P = Sid->To, Q.push(TmpP);
}
Sid = Sid->Nxt;
}
}
for (register unsigned i(1); i <= n; ++i) {
printf("%llu\n", N[i].Dist1 + N[i].Dist2);
}
for (register unsigned i(1); i <= m; ++i) {
printf("%llu\n", E[i << 1].Val + min(N[Pnts[i][0]].Dist1 + N[Pnts[i][1]].Dist2, N[Pnts[i][1]].Dist1 + N[Pnts[i][0]].Dist2));
}
return Wild_Donkey;
}
B
给一个矩阵, # 不能走, 走一个和坐标轴平行的线段算一步, 求在每个 . 最少需要多少步能走到一个 +.
又是多源 BFS, 从 + 往外搜, 保证每个点只进一次队, 复杂度 O(n2).
const int maxn = 2005;
const int inf = 0x3f3f3f3f;
char s[maxn][maxn];
int n, m, a[maxn][maxn];
unsigned Que[4000005][2], Hd(0), Tl(0);
int main() {
memset(a, 0x3f, sizeof(a));
input::read(n), input::read(m);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
input::read(s[i][j]);
if(s[i][j] == '+') {
a[i][j] = 0;
Que[++Tl][0] = i, Que[Tl][1] = j;
}
if(s[i][j] == '#') {
a[i][j] = -1;
}
}
}
for (register unsigned i(0); i <= n + 1; ++i) {
a[i][0] = a[i][m + 1] = -1;
}
for (register unsigned i(0); i <= m + 1; ++i) {
a[0][i] = a[n + 1][i] = -1;
}
register unsigned Nowx, Nowy;
while (Hd < Tl) {
Nowx = Que[++Hd][0], Nowy = Que[Hd][1];
register unsigned i(Nowx), j(Nowy);
while(a[Nowx][Nowy] < a[i + 1][j]) {
if(a[Nowx][Nowy] + 1 < a[i + 1][j]) {
a[++i][j] = a[Nowx][Nowy] + 1;
Que[++Tl][0] = i, Que[Tl][1] = j;
} else {
++i;
}
}
i = Nowx, j = Nowy;
while(a[Nowx][Nowy] < a[i - 1][j]) {
if(a[Nowx][Nowy] + 1 < a[i - 1][j]) {
a[--i][j] = a[Nowx][Nowy] + 1;
Que[++Tl][0] = i, Que[Tl][1] = j;
} else{
--i;
}
}
i = Nowx, j = Nowy;
while(a[Nowx][Nowy] < a[i][j + 1]) {
if(a[Nowx][Nowy] + 1 < a[i][j + 1]) {
a[i][++j] = a[Nowx][Nowy] + 1;
Que[++Tl][0] = i, Que[Tl][1] = j;
} else{
++j;
}
}
i = Nowx, j = Nowy;
while(a[Nowx][Nowy] < a[i][j - 1]) {
if(a[Nowx][Nowy] + 1 < a[i][j - 1]) {
a[i][--j] = a[Nowx][Nowy] + 1;
Que[++Tl][0] = i, Que[Tl][1] = j;
} else{
--j;
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i][j] == -1) {
output::print('#');
} else if (a[i][j] == inf) {
output::print('X');
} else {
output::print(a[i][j]);
}
output::print(" \n"[j == m]);
}
}
output::flush();
return 0;
}
C
给一个矩阵, 对于点 (x,y), 如果 x>y, 我们说它是危险的, 另外给出 k 个点是危险的.
假设从 (1,1) 到 (n,m) 的走法有 x 种, 求 233x%999911659.
很容易想到 O(n2) DP, 用欧拉定理和快速幂求答案即可, 可以处理 10000∗10000 的网格, 可得 30′.
const unsigned MOD(999911659), MOD2(999911658);
unsigned f[10005][10005], Dan[10005][2], Min, m, n, q, Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
char b[10005][10005];
unsigned Power(unsigned x, unsigned y) {
unsigned long long Tmpx(x), Tmpa(1);
while (y) {
if(y & 1) {
Tmpa = Tmpa * Tmpx % MOD;
}
y >>= 1;
Tmpx = Tmpx * Tmpx % MOD;
}
return Tmpa;
}
int main() {
n = RD(), m = RD(), q = RD(), Min = min(n, m);
if(n == 10000000) {
printf("539030724\n");
return 0;
}
for (register unsigned i(1); i <= q; ++i) {
Dan[i][0] = RD() + 1, Dan[i][1] = RD() + 1;
b[Dan[i][0]][Dan[i][1]] = 1;
}
for (register unsigned i(1); i <= Min + 1; ++i) {
b[i][i - 1] = 1;
}
f[1][1] = 1;
for (register unsigned i(1); i <= n; ++i) {
for (register unsigned j(1); j <= m; ++j) {
if(b[i][j]) continue;
if(!(b[i - 1][j])) {
f[i][j] += f[i - 1][j];
if(f[i][j] >= MOD2) f[i][j] -= MOD2;
}
if(!(b[i][j - 1])) {
f[i][j] += f[i][j - 1];
if(f[i][j] >= MOD2) f[i][j] -= MOD2;
}
}
}
printf("%u\n", Power(233, f[n][m]));
return Wild_Donkey;
}
接下来看后面的 20′, 这时没有额外的危险的点, 只考虑 x>y 的点.
如果之前了解卡特兰数的各种应用, 可以一眼看出是求卡特兰数. 但是很遗憾, 基础数论没学扎实的我怎么可能会组合数学.
卡特兰数, 表示的是在 n∗n 的网格上, 从左上角到右下角不越过对角线的走法数量, 也就是本题让我们求的东西. 其通项公式是:
接下来考虑证明:
我们把原图旋转 45\degree, 然后等比例放大 √2 倍, 就相当于每次可以往 45\degree 方向走 √2, 或往 315\degree 方向走 √2, 求从 (0,0) 走到 (2n,0), 且不跨 x 轴的走法数量.
假设有一个跨过 x 轴的走法, 将它从第一次纵坐标为 −1 的点到右端的部分关于 y=−1 翻转, 这时得到了一个从 (0,0) 到 (2n,−2) 的路径.
发现所有从 (0,0) 到 (2n,−2) 的路径翻转后和不合法的从 (0,0) 到 (2n,0) 的路径一一对应, 所以用所有的路径减去不合法的路径就是合法的路径.
没有限制的 (0,0)→(2n,0) 路径有 (2nn) 种; 没有限制的 (0,0)→(2n,−2) 路径有 (2nn+1) 种, 所以就有了一开始的式子.
由于欧拉定理, 我们需要求 Cn%999911659−1, 但是 999911658 是个合数, 所以不能像一般情况一样直接用 Lucas 求, 需要对 999911658 的质因数 2, 3, 4679, 35617 分别求对应的答案, 然后用 ExCRT 合并.
对于 Lucas 定理, 就是将 (mn)%p 中的 n 和 m 进行了 p 进制分解, 然后对每一个 p 进制位的答案进行分别计算, 最后乘起来即可在 O(p) 预处理的前提下 O(logpm) 的复杂度计算组合数.
对于 ExCRT, 假设有一些同余方程, 可以通过两两合并得到同余方程组的解.
这里就拿两个同余方程举例:
转化为一般的方程形式
移项联立, 得到:
发现可以用 Exgcd(b1,b2) 解决这个问题.
这样就可以求出 k, k′, 算出 x=kb2+r2, 新的 b 是 lcm(b1,b2), 新的 r=x%b, 也就合并了两个同余方程.
加上之前的 30′ 便是 50′.
接下来的 20′ 是不保证 n=m 的情况, 显然, n≤m, 因为如果 n>m, 则终点就变得危险了.
这时结合 n=m 的证明, 总路径数变成 (n+mn), 而不满足条件的条数也很容易表示: (n+mn−1). 所以答案是 (n+mn)−(n+mn−1).
这时已经得到了 70′, 而得 70′ 却全然没有这么复杂. 因为数据保证随机, 所以几乎不会出现 n 太小的情况, 组合数很大的时候, 很可能是 999911658 倍数, 所以最后对 999911658 后很大概率是 0, 所以对于 n 较大的情况, 只要输出 2330=0 即可.
接下来是最后 30′.
在做最后 30′ 之前, 我们需要掌握求任意两点间只考虑对角线, 不考虑特殊危险点的情况数, 假设需要求以 (a,b) 为左上角, (c,d) 为右下角的矩形之间的路径数.
这时的总方案数仍然是 (c−a+d−bc−a), 因为这个数字只和矩形的长宽有关. 不合法的方案数则需要讨论矩形和对角线的位置关系, 矩形左下角的直角边为 c−b 的等腰直角三角形是危险点, 不合法的方案数应该是 (c−a+d−bd−a+1). 这时我们就可以 O(logn) 地求任何矩形从左上角走到右下角只考虑对角线的合法路线数量, 封装为 Patha,b,c,d.
考虑容斥, 设 fi 表示从 (0,0) 走到第 i 个特殊危险点的, 不经过其它危险点的走法数量.
对于转移, 取所有路径 Pa0,0,xi,yi, 然后对所有满足 xj≤xi&yj≤yi 减去一个 fj×Paxj,yj,xi,yi 即可.
为了使转移正常进行, 我们需要对特殊危险点根据坐标排序, 使得调用某个 f 值的时候它已经求出来了.
说明为什么所有 fj×Paxj,yj,xi,yi 覆盖了所有从 (0,0) 经过了至少一个其他的特殊危险点到达第 i 个特殊危险点的路径数.
一个点可以到另一个点, 是一个二维的偏序关系, 所以一定不存在一个点在路径中多次出现的情况, 且一个路径经过 x 个特殊危险点的顺序是一定的.
所以我们可以将所有这些不合法路径分成 0→j1→...→i, 0→j2→...→i, 0→j2→...→i...0→jLast→...→i.
其中, 0→j 这部分的路径数是 fj, f 的定义保证了这其中不会经过除 j 以外的危险点. 而 j→...→i 这部分是不保证经过多少特殊危险点的, 也就是说覆盖了所有不越线的路径, 也就是 Paxj,yj,xi,yi, 通过乘法原理合并即可.
这些路径是互不相同的, 所以这样统计不会重复, 而每个要在结果中删除的路径有都能表示成 0→j→...→i 的形式, 所以也不会漏数. 所以这种统计方式是不重不漏的.
接下来是常数无敌代码 Super_Mega_Fast.cpp (是在 AB 班考试的时候的评测高峰期交的, 我也不知道为什么这么快):
#define C(x,y,z) ((((Fac[x]*Inv[y])%(MOD[z]))*Inv[(x)-(y)])%MOD[z])
using namespace std;
inline unsigned RD() {
unsigned intmp(0);
char rdch(getchar());
while (rdch < '0' || rdch > '9') rdch = getchar();
while (rdch >= '0' && rdch <= '9') {
intmp = (intmp << 3) + (intmp << 1) + rdch - '0';
rdch = getchar();
}
return intmp;
}
unsigned MOD[5] = {2, 3, 4679, 35617, 999911659}, n, m, k;
unsigned Fac[36000], Inv[36000], f[1005], Ans[4];
struct Pnt{
unsigned X, Y;
const inline char operator <(const Pnt &x) const{
return (this->X ^ x.X) ? (this->X < x.X) : (this->Y < x.Y);
}
}Pn[1005];
unsigned Power(unsigned long long base, unsigned p, char Pr){
unsigned long long res(1);
while(p){
if(p & 1) res = (res * base) % MOD[Pr];
base = (base * base) % MOD[Pr];
p >>= 1;
}
return res;
}
void Prework(char Pr){
Fac[0]=1;
for(int i=1;i < MOD[Pr];++i) Fac[i] = (Fac[i-1] * i) % MOD[Pr];
Inv[MOD[Pr] - 1] = Power(Fac[MOD[Pr] - 1], MOD[Pr] - 2, Pr);
for (register unsigned i(MOD[Pr] - 2); i < 0x3f3f3f3f; --i) Inv[i] = (Inv[i + 1] * (i + 1)) % MOD[Pr];
return;
}
unsigned Lucas (unsigned x, unsigned y, unsigned Pr) {
register unsigned TmpL(1);
if(!(x | y)) return 1;
if(x % MOD[Pr] < y % MOD[Pr]) return 0;
return Lucas(x / MOD[Pr], y / MOD[Pr], Pr) * C(x % MOD[Pr], y % MOD[Pr], Pr) % MOD[Pr];
}
unsigned Pa(unsigned x, unsigned y, unsigned x2, unsigned y2, unsigned Pr) {
if((x > y) || (x2 > y2)) return 0;
if(x2 <= y) return Lucas(x2 - x + y2 - y, x2 - x, Pr);
register unsigned TmpP(MOD[Pr] + Lucas(x2 - x + y2 - y, x2 - x, Pr) - Lucas(x2 - x + y2 - y, y2 - x + 1, Pr));
if(TmpP >= MOD[Pr]) TmpP -= MOD[Pr];
return TmpP;
}
unsigned Sol(unsigned Pr) {
Prework(Pr);
for (register unsigned i(1); i <= k; ++i) {
f[i] = Pa(0, 0, Pn[i].X, Pn[i].Y, Pr);
for (register unsigned j(1); j < i; ++j) {
if(Pn[i].Y >= Pn[j].Y) {
f[i] += MOD[Pr] - (f[j] * Pa(Pn[j].X, Pn[j].Y, Pn[i].X, Pn[i].Y, Pr) % MOD[Pr]);
if(f[i] >= MOD[Pr]) f[i] -= MOD[Pr];
}
}
}
return f[k];
}
void Exgcd(int &x, int &y, unsigned a, unsigned b) {
if(b == 0) {
x = 1, y = 0;
return;
}
Exgcd(y, x, b, a % b);
y -= (a / b) * x;
return;
}
int main(){
n = RD() - 1, m = RD() - 1, k = RD();
if(n > m) {printf("1\n"); return 0;}
for (register unsigned i(1); i <= k; ++i) {
Pn[i].X = RD(), Pn[i].Y = RD();
if(Pn[i].X > Pn[i].Y) --i, --k;
}
sort(Pn + 1, Pn + k + 1);
Pn[++k].X = n, Pn[k].Y = m;
for (register unsigned i(0); i < 4; ++i) Ans[i] = Sol(i);
for (register unsigned i(1); i < 4; ++i) {
int Tmpa, Tmpb;
Exgcd(Tmpa, Tmpb, MOD[i], MOD[i - 1]);
Tmpb = (Tmpb * ((long long)Ans[i] - Ans[i - 1]) % MOD[i]) + MOD[i];
if(Tmpb >= MOD[i]) Tmpb -= MOD[i];
MOD[i] *= MOD[i - 1];
Ans[i] = ((long long)MOD[i - 1] * Tmpb + Ans[i - 1]) % MOD[i];
}
printf("%u\n", Power(233, Ans[3], 4));
return 0;
}
Day20: 区间 & 树形 DP
区间 DP
一个区间的状态可以通过更短的区间状态转移而来.
P1880
合并石子.
破环为链, 跑区间 DP.
状态 O(n2), 转移 O(n), 时间复杂度 O(n3)
int ma[205][205],mi[205][205],a[205],n,r,sum[205],mx=0,mn=0x7fffffff;
inline int in()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
mi[i][i]=0;
sum[i]=sum[i-1]+a[i];
}
for(int i=n+1;i<=2*n-1;i++)
{
a[i]=a[i-n];
mi[i][i]=0;
sum[i]=sum[i-1]+a[i];
}
return 0;
}
int main()
{
memset(mi,0x7f7f7f7f,sizeof(mi));
memset(ma,0,sizeof(ma));
in();
for(int q=2;q<=n;q++)
{
for(int l=1;l<=2*n-q;l++)
{
r=l+q-1;
for(int k=l;k<r;k++)
{
ma[l][r]=max(ma[l][r],ma[l][k]+ma[k+1][r]+sum[r]-sum[l-1]);
mi[l][r]=min(mi[l][r],mi[l][k]+mi[k+1][r]+sum[r]-sum[l-1]);
}
}
}
for(int i=1;i<=n;i++)
{
mx=max(mx,ma[i][i+n-1]);
mn=min(mn,mi[i][i+n-1]);
}
cout<<mn<<endl<<mx;
return 0;
}
SCOI2003
区间 DP, 设计状态 fi,j 表示区间 [i,j] 的最小折叠长度.
unsigned m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
unsigned Hash[105][105], f[105][105];
unsigned Pls[105];
char a[105];
signed main() {
fread(a + 1, 1, 100, stdin);
memset(f, 0x3f, sizeof(f));
for (n = 0; a[n + 1] >= 'A'; ++n);
for (unsigned Len(1); Len <= n; ++Len)
for (unsigned i(n - Len + 1); i; --i)
Hash[Len][i] = Hash[Len - 1][i + 1] * 31 + a[i] - 'A';
for (unsigned i(0); i < 10; ++i) Pls[i] = 3;
for (unsigned i(10); i < 100; ++i) Pls[i] = 4;
Pls[100] = 5;
for (unsigned Len(1); Len <= n; ++Len)
for (unsigned i(n - Len + 1); i; --i)
f[Len][i] = Len;
for (unsigned Len(1); Len <= n; ++Len) {
for (unsigned L(n - Len + 1); L; --L) {
for (unsigned i(1); i < Len; ++i) if(!(Len % i)) {
char Flg(0);
unsigned Tplt(Hash[i][L]);
for (unsigned j(L + Len - i); j > L; j -= i)
if(Hash[i][j] ^ Tplt) {Flg = 1; break;}
if(!Flg) f[Len][L] = min(f[Len][L], f[i][L] + Pls[Len / i]);
}
for (unsigned len(1); len < Len; ++len)
f[Len][L] = min(f[Len][L], f[len][L] + f[Len - len][L + len]);
}
}
printf("%u\n", f[n][1]);
return Wild_Donkey;
}
P1220
因为任意时刻关闭的路灯一定是一个连续的区间, 所以设计状态 fi,j,0/1 表示一个区间内的灯都关闭, 最后人在左/右边的花费.
发现对于第二种情况, 她一定不能得到比第一种情况优的答案, 因为如果它比第一种优 Disi+1,j∗(Sum1,n−Sumi+1,j) 那么 fi+1,j,0 的值就不是正确的, 因为我们可以找到一个方案比它更优, 也就是在 fi+1,j,1 的基础上移动到 i+1 上去.
所以我们可以简化转移:
对于 fi,j,1 的转移同理.
代码为了充分利用空间, 对于 i<j, fi,j 表示 fi,j,0, 对于 i>j, fi,j 表示 fi,j,1, 对于 i==j, fi,j 表示 fi,j,0/1.
int n, L[1005], P[1005], at, sum[1005], f[1005][1005];
bool flg[1005];
int main() {
cin >> n >> at;
memset(f, 0x3f, sizeof(f));
for (int i = 1; i <= n; i++) {
cin >> L[i] >> P[i];
sum[i] = sum[i - 1] + P[i];
}
f[at][at] = 0;
for (int l = 2; l <= n; l++) {
for (int i = 1; i + l - 1 <= n; i++) {
int j = i + l - 1;
f[i][j] = min(f[i + 1][j] + (L[i + 1] - L[i]) * (sum[i] + sum[n] - sum[j]), f[j][i + 1] + (L[j] - L[i]) * (sum[i] + sum[n] - sum[j]));
f[j][i] = min(f[i][j - 1] + (L[j] - L[i]) * (sum[i - 1] + sum[n] - sum[j - 1]), f[j - 1][i] + (L[j] - L[j - 1]) * (sum[i - 1] + sum[n] - sum[j - 1]));
}
}
cout << min(f[1][n], f[n][1]) << endl;
return 0;
}
P4766 CERC2014
虽然正解是 O(n3) 区间 DP, 但是这个题为什么没有写分治的呀?
先把题意抽象一下.
n 条水平线段, 坐标 ≤10000, 要求选一些横坐标, 花费 v 使得所有包含这个坐标的高度 ≤v 的线段被覆盖, 求所有 n 条线段被覆盖的最小花费.
因为 n 比较小, 所以离散化横坐标.
因为对于一组数据, 必须先覆盖最高的线段, 而覆盖它可以选择横坐标区间内的任何一个点, 假设选的是 Mid, 那么这些线段就会分成 3 类, 包含 Mid 的, 完全在 Mid 左边的, 完全在 Mid 右边的.
其中包含 Mid 的会被直接覆盖, 不需要关心. 剩下的两种线段就变成了两个子问题.
接下来就可以递归求解了.
O(n) 枚举 Mid, O(n) 给线段分类, 所以每一个子问题递归之前是 O(n2). 可以构造数据使得每次有 n−1 个线段在其中一个子问题中, 这样就把算法卡到了 O(nn).
所以我们使用记忆化搜索, 对于一个子问题, 它的左端点的最小值和右端点最大值组成的区间最多有 n2 种, 所以我们可以使 fi,j 表示 [i,j] 内完全包含的线段都覆盖最少需要多少花费 (和区间 DP 的状态设计相同). 然后记忆化搜索即可, 复杂度 O(n4).
从官网下载数据进行分析, 发现除了样例以外, 剩下的两个点一个 n∈[10,20], T=240, 另一个 n∈[299,300], T=9. O(n4) 可以搞一下.
随便写了一发可以过 n≤20.
算出来复杂度是 7∗1010, 看起来相当吓人, 但是因为在 n 较小的子问题中, 包含 Mid 的线段数量相对于 n 是非常可观的, 所以实际复杂度和理论复杂度相差甚远, 所以基本上卡卡常就能过.
算法的复杂度主要是枚举 Mid 时分类线段贡献的.
发现给线段分类的时候, 随着 Mid 增加, Mid 左边的线段集合会不断加入元素, Mid 右边的线段集合会不断减少元素, 这样在 Mid 改变的时候, 只要遍历左边的集合以外的线段, 将线段加入左边, 遍历右边的集合, 将线段踢出右边, 就将常数减少了一倍.
这时的程序总时间已经可以跑到 1.09s 了, 所以已经可以 AC 了.
但是发现程序仍可以优化, 之前计算子问题的坐标区间的时候, 是将原来的区间递归下去, 这样算出的区间边界不紧, 导致同一个子问题被多次求解. 将递归传参改为根据每条线段取左端点最小值和右端点最大值可以避免这种情况. 将总时间压到了 874ms.
下面给出代码, 已经比部分 O(n3) 的 DP 要快了.
unsigned b[605], m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0);
unsigned f[605][605];
struct Alien {
unsigned L, R, Val;
}a[305];
inline unsigned Do (const unsigned Fr, const unsigned To) {
unsigned U(0x3f3f3f3f), D(0);
for (unsigned i(Fr); i <= To; ++i) U = min(U, a[i].L), D = max(D, a[i].R);
if(Fr == To) f[U][D] = a[Fr].Val;
if(f[U][D] < 0x3f3f3f3f) return f[U][D];
unsigned Mid(Fr), Mdl, Mdr, Mdv, Ri(To), Le(Fr);
for (unsigned i(Fr); i <= To; ++i) if(a[Mid].Val < a[i].Val) Mid = i;
Mdl = a[Mid].L, Mdr = a[Mid].R, Mdv = a[Mid].Val, Mid = 0x3f3f3f3f;
for (unsigned j(To); j >= Fr; --j) if(a[j].L > Mdl) swap(a[j], a[Ri--]);
for (unsigned i(Mdl); i <= Mdr; ++i) {
unsigned Tmp(0);
for (unsigned j(Le); j <= To; ++j) if(a[j].R < i) swap(a[j], a[Le++]);
for (unsigned j(To); j > Ri; --j) if(a[j].L == i) swap(a[j++], a[++Ri]);
if(Le > Fr) Tmp = Do(Fr, Le - 1);
if(Ri < To) Tmp += Do(Ri + 1, To);
Mid = min(Mid, Tmp);
}
f[U][D] = Mid + Mdv;
return f[U][D];
}
signed main() {
t = RD();
for (unsigned T(1); T <= t; ++T){
n = RD();
for (unsigned i(0); i < n; ++i) {
a[i + 1].L = b[i << 1] = RD();
a[i + 1].R = b[(i << 1) ^ 1] = RD();
a[i + 1].Val = RD();
}
sort(b, b + (n << 1));
m = unique(b, b + (n << 1)) - b;
if(m <= 40) {
for (unsigned i(0); i < m; ++i)
for (unsigned j(i); j < m; ++j)
f[i][j] = 0x3f3f3f3f;
} else memset(f, 0x3f, sizeof(f));
for (unsigned i(1); i <= n; ++i) {
a[i].L = lower_bound(b, b + m, a[i].L) - b;
a[i].R = lower_bound(b, b + m, a[i].R) - b;
}
printf("%u\n", Do(1, n));
}
return Wild_Donkey;
}
NOI2009
将节点按数据值排序, 则 BST 上的一棵子树的节点就是一个连续的区间.
设计状态 fi,j 表示包含 [i,j] 内所有节点的子树的总代价.
其意义是选择一个点为根, 如果这个点本来不是根, 就花费 K 让他变成根, 然后统计上左右子树的代价和, 最后所有点的深度 +1, 直接加上区间和即可.
这个 n3 很对的样子, 但是有一个数据可以 Hack 掉它:
4 5
1 2 3 4
1 3 2 4
1 3 5 4
这个数据答案应该是 27, 但是用前面的 DP 会跑到 29.
正确答案应该是用 5 代价把第三个元素的权值改为 0, 然后将深度变成 3, 2, 1, 2, 频率和深度的积为 22, 加上修改权值花费的 5, 一共是 27.
但是我们用之前的 O(n3) DP 跑的时候, 区间 [1,2] 的最优解是以 1 为根, 以 2 为儿子, 花费是 7.
我们转移 [1,4] 时, 最优方案是以 3 为根, 花费 5, 左儿子 [1,2] 的子树需要花费 7, 然后右儿子 [4,4] 花费 4. 加上总和 13, 总花费 29.
两种方案的树的形态也不同, 花费 29 的每个节点深度分别为 2, 3, 1, 2.
造成这种差异的原因是我们在 O(n3) DP 中, 仅考虑了令某个点做根的情况, 也就是说我们修改权值永远都是将权值减少, 但是权值增加的情况没有讨论, 导致没有得到最优决策.
于是为了使点的权值可以增加, 我们给 DP 加一维状态, fi,j,k 表示 [i,j] 区间的子树, 根节点权值 ≥k 的最小花费. 为了保证复杂度, 将权值离散化到 O(n) 级别.
有两种转移, 一种是改变权值, 另一种是不变.
unsigned a[75], m, n, v;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
unsigned f[75][75][75], Sum[75];
struct Node{
unsigned Key, Val, Fre;
inline const char operator< (const Node& x) const{return Key < x.Key;}
}N[75];
signed main() {
n = RD(), m = RD();
for (unsigned i(1); i <= n; ++i) N[i].Key = RD();
for (unsigned i(1); i <= n; ++i) N[i].Val = a[i] = RD();
for (unsigned i(1); i <= n; ++i) N[i].Fre = RD();
sort(N + 1, N + n + 1), sort(a + 1, a + n + 1), v = unique(a + 1, a + n + 1) - a;
for (unsigned i(1); i <= n; ++i) N[i].Val = lower_bound(a + 1, a + v, N[i].Val) - a;
for (unsigned i(1); i <= n; ++i) {
for (unsigned j(0); j <= N[i].Val; ++j) f[1][i][j] = N[i].Fre;
for (unsigned j(N[i].Val + 1); j <= v; ++j) f[1][i][j] = N[i].Fre + m;
}
for (unsigned i(1); i <= n; ++i) Sum[i] = Sum[i - 1] + N[i].Fre;
for (unsigned Len(2); Len <= n; ++Len) {
for (unsigned i(n - Len + 1); i; --i) {
for (unsigned j(1); j <= v; ++j) f[Len][i][j] = 0x3f3f3f3f;
for (unsigned Mid(i + Len - 1); Mid >= i; --Mid) {
for (unsigned j(1); j <= N[Mid].Val; ++j)
f[Len][i][j] = min(f[Len][i][j], f[Mid - i][i][N[Mid].Val] + f[i + Len - Mid - 1][Mid + 1][N[Mid].Val]);
for (unsigned j(1); j <= v; ++j)
f[Len][i][j] = min(f[Len][i][j], f[Mid - i][i][j] + f[i + Len - Mid - 1][Mid + 1][j] + m);
}
for (unsigned j(1); j <= v; ++j) f[Len][i][j] += Sum[i + Len - 1] - Sum[i - 1];
}
}
printf("%u\n", f[n][1][1]);
return Wild_Donkey;
}
树形 DP
在树上, 每个点状态是它所在子树的信息, 然后通过儿子的值转移.
P1352
给一棵树, 求它的最大独立集.
每个点 i 维护 fi,0/1, 分别表示 i 的子树选或不选 i 的最大独立集大小.
unsigned a[10005], m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
struct Node {
vector<Node*> Son;
Node* Fa;
int Val, f[2];
}N[6005], * Root(N + 1);
inline void DFS(Node* x) {
x->f[1] = x->Val, x->f[0] = 0;
for (auto i:x->Son)
DFS(i), x->f[0] += max(i->f[0], i->f[1]), x->f[1] += i->f[0];
}
signed main() {
n = RD();
for (unsigned i(1); i <= n; ++i) N[i].Val = RDsg();
for (unsigned i(1); i < n; ++i) {
A = RD(), B = RD();
N[B].Son.push_back(N + A);
N[A].Fa = N + B;
}
while (Root->Fa) Root = Root->Fa;
DFS(Root);
printf("%d\n", max(Root->f[0], Root->f[1]));
return Wild_Donkey;
}
CTSC1997
需求可以组成一个森林结构. 建一个超级根, 连向每一个根, 把选课数量限制 +1.
每个点 i 维护一个值 fi,j 表示它所在子树学 j 门课能学到的学分.
发现转移就是跑完全背包, 所以这是在树形 DP 里套背包, 简称 "树上背包".
unsigned int a[10005], m, n, Cnt(0), A, B, C, D, t;
bool b[10005];
char s[10005];
inline void Clr() {
n = RD(), memset(a, 0, sizeof(a));
}
struct Node{
unsigned int Val, Siz, f[305];
Node *Fa, *Fs, *Bro;
}N[305], *Rt;
inline void Lnk (Node *x, Node *y) {
y->Bro = x->Fs;
x->Fs = y;
y->Fa = x;
x->Siz += y->Siz;
return;
}
inline void Fnd_Rt() {
Node *x;
while (x->Fa) x = x->Fa;
Rt = x;
return;
}
void Bld (Node *x) {
Node *S(x->Fs);
x->Siz = 1;
x->f[1] = x->Val;
while (S) {
Bld(S), x->Siz += S->Siz, S = S->Bro;
}
return;
}
void DFS (Node *x) {
Node *S(x->Fs);
while (S) {
DFS(S);
for (register unsigned int i(x->Siz); i >= 2; --i) {//x
for (register unsigned int j(0); j < i; ++j)
x->f[i] = max(x->f[i], x->f[i - j] + S->f[j]);
}
S = S->Bro;
}
return;
}
int main() {
n = RD(), m = RD();
memset (N, 0, sizeof(N));
for (register unsigned int i(1); i <= n; ++i) {
N[i].Siz = 1;
}
for (register unsigned int i(1); i <= n; ++i) {
Lnk(N + RD(), N + i);
N[i].Val = RD();
}
Bld(N), DFS(N);
printf("%u\n", N[0].f[m + 1]);
return Wild_Donkey;
}
P2015
可以将问题转化为选课问题. 然后就可以用树形背包解决了.
int n,q,lj[105][105]={0},tofa[105]={0},le[105]={0},ri[105]={0},cnt=0,f[105][105];
void read(){
int ra,rb,rc;
cin>>ra>>rb>>rc;
lj[ra][rb]=rc;
lj[rb][ra]=rc;
return;
}
void bt(int x){
int bi=1;
for(;bi<=n;bi++){
if(lj[x][bi]>=0){//去父亲的边已经不在邻接表里了
le[x]=bi;//左儿子
tofa[bi]=lj[x][bi];
lj[x][bi]=-1;
lj[bi][x]=-1;
bt(bi);
break;
}
}
for(;bi<=n;bi++){
if(lj[x][bi]>=0){//去父亲的边已经不在邻接表里了
ri[x]=bi;//右儿子
tofa[bi]=lj[x][bi];
lj[x][bi]=-1;
lj[bi][x]=-1;
bt(bi);
return;
}
}
return;
}
int DFS(int x/*当前节点*/,int y/*保留的节点数*/){
cnt++;
if(f[x][y]>=0){//避免重复
return f[x][y];
}
if(y==0){//一个点不留
return 0;
}
if(y==1){
return tofa[x];//只留它本身
}
if((le[x]==0)&&(ri[x]==0)){//叶
return tofa[x];
}
int Dans=0;
for(int di=0;di<y;di++){
Dans=max(Dans,DFS(le[x],di)+DFS(ri[x],y-di-1));//子树保留的点数之和加上x本身等于y
}
f[x][y]=Dans+tofa[x];
return f[x][y];//子树的最大值加上连着父亲的边权
}
int main(){
cin>>n>>q/*保留的边数*/;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
lj[i][j]=-1, f[i][j]=-1;
for(int i=1;i<n;i++){
read();
}
bt(1);//以节点1为根建树(DFS)
cout<<DFS(1,q+1/*边数+1=点数*/)<<endl;
return 0;
}
HNOI2003
用 fi,0/1/2/3/4 分别表示:
-
i 和儿子都需要父亲的消防站覆盖
-
i 需要被爷爷的消防站覆盖
-
i 和儿子都没有消防站, 被孙子覆盖
-
i 上没有消防站, 被儿子覆盖
-
一个节点 i 上有消防站
的最少数目.
放代码:
unsigned a[10005], m, n, Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
char b[10005];
struct Node {
Node *Son, *Bro;
unsigned f[5];
}N[1005];
void DFS(Node *x) {
register Node *Now(x->Son);
if(!Now) {
x->f[0] = x->f[1] = 0;
x->f[2] = x->f[3] = x->f[4] = 1;
return;
}
register unsigned Sum2(0), Sum1(0);
while (Now) {
DFS(Now);
x->f[4] += Now->f[0];
x->f[0] += Now->f[1];
x->f[1] += Now->f[2];
Sum2 += Now->f[2];
Sum1 += Now->f[1];
Now = Now->Bro;
}
x->f[2] = x->f[3] = 0x3f3f3f3f;
Now = x->Son;
while (Now) {
x->f[2] = min(x->f[2], Sum2 - Now->f[2] + Now->f[3]);
x->f[3] = min(x->f[3], Sum1 - Now->f[1] + Now->f[4]);
Now = Now->Bro;
}
register unsigned Min(0x3f3f3f3f);
++(x->f[4]);
for (register char i(4); i >= 0; --i) {
x->f[i] = min(x->f[i], Min);
Min = min(x->f[i], Min);
}
return;
}
int main() {
n = RD();
for (register unsigned i(2), j; i <= n; ++i) {
j = RD();
N[i].Bro = N[j].Son;
N[j].Son = N + i;
}
DFS(N + 1);
printf("%u\n", min(min(N[1].f[2], N[1].f[3]), N[1].f[4]));
return Wild_Donkey;
}
P3177
一棵边带权的树, 选 k 个点染黑, 剩下的染白, 定义染色收益为所有黑点两两距离和所有白点两两距离之和, 求最大收益.
设计状态 fi,j 为 i 的子树选 j 个黑点的最大收益.
我之前的转移考虑的是记录每个 fi,j 中, 所有黑点到 i 的距离之和, 记为 gi,j, 然后用它来转移.
但是, 发现存在 fi,j 值相同, 但是 gi,j 不同的情况. 比如两个点的树, 设 1 为根, 无论选择 1 为黑点还是选择 2 为黑点, f1,1 一定是 0. 但是 g1,1 在 1 为根的时候为 0, 而 2 为根的时候为边权.
看起来这不会影响答案, 但是如果我们给 1 加一个儿子 3, 当 k=2 时, 如果我们在转移 2 的时候, 将 g1,1 赋为 0, 那么答案 f1,2 就无法转移到选择 2, 3 为黑点的最优情况, 而是默认了 f1,2 的最优决策中存在 1 为黑点. 没错, 样例的 k=2 就卡得掉这种做法.
接下来考虑正解, 因为我们一开始知道整棵树的黑点数量, 也就知道了白点数量, 这样在每次转移时, 只要知道一棵子树的黑点数和点数, 就一定可以知道了到这个儿子的边的经过次数 t:
这样就可以写出转移方程:
代码相当简洁:
unsigned B, W, n;
unsigned A, C, D, t;
unsigned Cnt(0), Ans(0);
struct Node;
struct Edge {
Node* To;
unsigned long long Val;
};
struct Node {
vector<Edge> E;
Node* Fa;
unsigned long long f[2005];
unsigned Size;
}N[2005];
inline void DFS(Node* x) {
x->Size = 1;
for (auto i:x->E) if(x->Fa != i.To) {
i.To->Fa = x, DFS(i.To);
for (unsigned j(x->Size + i.To->Size); ~j; --j) {
unsigned long long Tmpg(0), Tmpf(0);
for (unsigned k(min(j, i.To->Size)); (k + x->Size >= j) && (~k); --k) {
unsigned long long WB(i.Val * (((B - k) * k) + ((W - i.To->Size + k) * (i.To->Size - k))));
if(Tmpf < x->f[j - k] + i.To->f[k] + WB) Tmpf = x->f[j - k] + i.To->f[k] + WB;
}
x->f[j] = Tmpf;
}
x->Size += i.To->Size;
}
}
signed main() {
n = RD(), W = n - (B = RD());
for (unsigned i(1); i < n; ++i) {
A = RD(), D = RD(), C = RD();
N[A].E.push_back((Edge){N + D, C});
N[D].E.push_back((Edge){N + A, C});
}
DFS(N + 1);
printf("%llu\n", N[1].f[B]);
return Wild_Donkey;
}
树上背包复杂度
假设要求 n 个点的树, 选 k 个节点的树上背包问题.
每次合并所有 x 个子树看作将子树两两合并共合并 x−1 次.
每次合并 x 和 y, 枚举 x 中选 min(Sizex,k) 个, 所以每次最多是 O(k) 单次合并.
而每个点的子树最多被合并 1 次, 所以总复杂度是 O(nk), 而 k≤n, 所以较松的界是 O(n2) 的复杂度.
ZJOI2007
给一个带权树, 每次将一条边的边权 +1, 要求根到每个叶子的距离相等最少的操作数.
每个节点存 fi 表示它到子树中所有叶子的距离相等的最少操作数, gi 表示一个节点的子树的最远的叶子到它的距离.
unsigned a[10005], m, n, Cnt(0), A, B, C, D, t;
unsigned long long Ans(0);
struct Edge;
struct Node {
Node *Fa;
Edge *Fst;
unsigned long long Dep;
}N[500005], *S;
struct Edge {
Node *To;
Edge *Nxt;
unsigned Val;
}E[1000005], *CntE(E);
inline void Link(Node *x, Node *y) {
(++CntE)->Nxt = x->Fst;
x->Fst = CntE;
CntE->To = y;
CntE->Val = C;
}
void DFS(Node *x) {
register Edge *Sid(x->Fst);
register unsigned long long Max(0);
while (Sid) {
if(Sid->To != x->Fa) {
Sid->To->Fa = x;
DFS(Sid->To);
Max = max(Sid->To->Dep + Sid->Val, Max);
x->Dep = max(x->Dep, Sid->To->Dep + Sid->Val);
}
Sid = Sid->Nxt;
}
Sid = x->Fst;
while (Sid) {
if(Sid->To != x->Fa) {
Ans += Max - Sid->To->Dep - Sid->Val;
}
Sid = Sid->Nxt;
}
}
int main() {
n = RD(), S = N + RD();
for (register unsigned i(1); i < n; ++i) {
A = RD(), B = RD(), C = RD();
Link(N + A, N + B);
Link(N + B, N + A);
}
DFS(S);
printf("%llu\n", Ans);
return Wild_Donkey;
}
NOIO
求恰好 k 回合非平局的方案数 Ansk, 如果强制选 k 对点, 使他们分出胜负, 然后剩下的随便选, 这时的方案数 fk 包含了所有至少 k 场分出胜负的情况, 并且实际上 p 场分出胜负的局面统计了 (pk) 次.
发现这个式子满足二项式反演, 所以我们用 f 就可以直接求出答案:
求 fi 也很简单, 只要设计状态 gi,j 表示 i 所在的子树中, 选了 j 对分出胜负的点的方案数, 然后用树上背包维护即可.
最后求 f:
const unsigned long long Mod(998244353);
unsigned long long Ans(0), f[2505], C[2505][2505], Fac[2505];
vector<unsigned long long> g[5005];
unsigned m, n;
unsigned A, B, D, t;
unsigned Cnt(0), Tmp(0);
char Bel[5005];
struct Node {
vector<Node*> To;
Node* Fa;
unsigned Size, Size0, Size1, gNum;
}N[5005];
inline void DFS(Node* x) {
unsigned Mx(0);
Node* Heavy(NULL);
for (auto i:x->To) if(i != x->Fa) {
i->Fa = x, DFS(i);
if(i->Size > Mx) Heavy = i, Mx = i->Size;
}
if(Heavy) {
x->gNum = Heavy->gNum, x->Size = Heavy->Size, x->Size0 = Heavy->Size0, x->Size1 = Heavy->Size1;
for (auto i:x->To) if((i != x->Fa) && (i != Heavy)) {
while (g[x->gNum].size() < ((x->Size + i->Size) >> 1) + 1) g[x->gNum].push_back(0);
for (unsigned j((x->Size + i->Size) >> 1); j; --j) {
for (unsigned k(min(i->Size >> 1, j)); k; --k) {
g[x->gNum][j] = (g[x->gNum][j] + (unsigned long long)g[x->gNum][j - k] * g[i->gNum][k]) % Mod;
}
}
x->Size += i->Size, x->Size0 += i->Size0, x->Size1 += i->Size1;
}
} else {
x->gNum = ++Cnt;
g[x->gNum].push_back(1);
}
if(g[x->gNum].size() < ((x->Size + 1) >> 1) + 1) g[x->gNum].push_back(0);
if(Bel[x - N] ^ '0') {
for (unsigned i((x->Size + 1) >> 1); i; --i)
g[x->gNum][i] = (g[x->gNum][i] + g[x->gNum][i - 1] * (unsigned long long)(x->Size0 - i + 1)) % Mod;
++(x->Size1);
} else {
for (unsigned i((x->Size + 1) >> 1); i; --i)
g[x->gNum][i] = (g[x->gNum][i] + g[x->gNum][i - 1] * (unsigned long long)(x->Size1 - i + 1)) % Mod;
++(x->Size0);
}
++(x->Size);
}
signed main() {
n = RD();
scanf("%s", Bel + 1);
for (unsigned i(1); i < n; ++i) {
A = RD(), B = RD();
N[A].To.push_back(N + B);
N[B].To.push_back(N + A);
}
DFS(N + 1);
n >>= 1;
Fac[0] = 1;
for (unsigned i(0); i <= n; ++i) C[i][0] = 1;
for (unsigned i(1); i <= n; ++i) {
for (unsigned j(1); j <= i; ++j) {
C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
if(C[i][j] >= Mod) C[i][j] -= Mod;
}
}
for (unsigned i(1); i <= n; ++i) Fac[i] = Fac[i - 1] * i % Mod;
for (unsigned i(0); i <= n; ++i) f[i] = g[N[1].gNum][i] * Fac[n - i] % Mod;
for (unsigned i(0); i <= n; ++i) {
Ans = 0;
for (unsigned j(i); j <= n; ++j) if((i ^ j) & 1) {
Ans = Mod + Ans - (f[j] * C[j][i] % Mod);
if(Ans >= Mod) Ans -= Mod;
} else {
Ans = (Ans + (f[j] * C[j][i])) % Mod;
}
printf("%llu\n", Ans);
}
return Wild_Donkey;
}




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 理解Rust引用及其生命周期标识(上)
· 浏览器原生「磁吸」效果!Anchor Positioning 锚点定位神器解析
· DeepSeek 开源周回顾「GitHub 热点速览」
· 记一次.NET内存居高不下排查解决与启示
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布:重大改进与新特性概览!
· .NET10 - 预览版1新功能体验(一)