第三种树链剖分: 长链剖分

长链剖分

树链剖分可以分为三种, 分别是重链剖分, 动态树 (实链剖分) 和长链剖分 (Long Path Decomposition).

长链剖分的规则是将子树包含最深的后代的儿子设为 "长儿子", 然后将到长儿子的边称 "长边", 长边组成的链称 "长链", 其余的边都是 "短边". 和重链剖分类似, 长链的长度定义为它包含的节点数, 或是长边数 $+1$.

前两种剖分方式, 在绝大多数题目中可以相互代替, 但是长链剖分的应用却和它们不同.

路径短边数量

考虑如何使用最少的节点数, 构造一棵树, 让它在长链剖分后, 根到某个叶子的路径上, 短边数量最多.

依然是重链剖分的构造方式, 从边界情况开始考虑:

• 根到叶子最多有 $0$ 个短边, 最少需要 $0$ 个点.

连点都不用就构造完了, 没什么好解释的.

• 根到叶子最多有 $1$ 个短边, 最少需要 $3$ 个点.

一个根, 左右儿子都是单点, 这时, 两个儿子必有一个是长儿子, 另一个是短儿子, 有一个短边.

• 根到叶子最多有 $2$ 个短边, 最少需要 $6$ 个点.

在上一棵树的基础上, 在根上接一个父亲作为新的根, 在这个根下面接一个长度为 $2$ 的垂直的链作为长链, 则旧根可以做新根的短儿子.

• 根到叶子最多有 $k$ 个短边, 最少需要 $\frac {(k + 1)(k + 2)}2$ 个点.

发现以这种构造方式, 每次可以从根到叶子最多 $k - 1$ 个短边的树的基础上, 接一个根节点, 再接一条长度为 $k - 1$ 的长链. 这样, 所需的点数便成了等差数列求和, 所以得到式子 $\frac {(k + 1)(k + 2)}2$.

举个例子, 这是一棵到叶子最多有 $3$ 个短边的树, 短边分别是: 6-3, 3-2, 2-0.

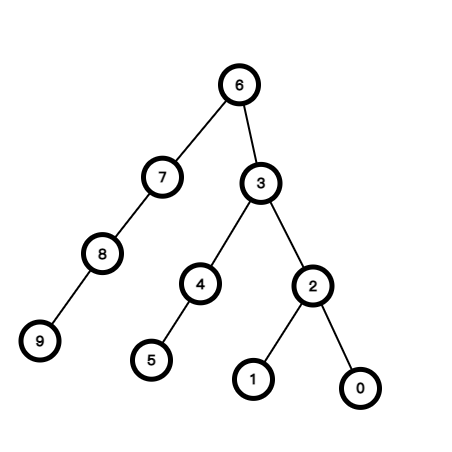
因此, 对于一棵 $n$ 个节点的树, 根到叶子路径上最多的短边数量为 $O(\sqrt n)$.

主要应用: $O(1)$ 求树上第 $k$ 级祖先

由于长链剖分的特殊性质: 一个长链链顶的子树的深度就是这个长链的长度. 所以可以保证一个点 $x$ 的 $a$ 级祖先所在的长链长度至少有 $a$. 这个结论很好证明, 只要假设这个长链长度小于 $a$, 则 $x$ 点到它的 $a$ 级祖先的路径必然是长度为 $a$ 的长链.

对于剖分后的每个点, 分配一个 DFS 序, 保证在长链上的相邻的点的 DFS 序相邻.

对于一棵 $n$ 个点的树, 可以建立一个长度为 $n$ 的数组 $List$, 对于每个长链, 设它的长度为 $l$ 设它链顶的 DFS 序为 $x$, 则 $List$ 的第 $[x, x + l)$ 的位置, 依次存 $x$ 的第 $[0, l)$ 级祖先.

再记录一个数组 $InList$, 使得 $InList_i$ 表示 DFS 序为 $i$ 的点的编号. 因为长链剖分的性质, 对于一个长链链顶 $x$ (它的 DFS 序为 $x$), $InList$ 的第 $[x, x + l)$ 位表示它的 $[0, l)$ 级长链上后代.

接下来, 和倍增求 LCA 一样, 求每个节点的 $2^a$ 级祖先, 预处理复杂度 $O(nlogn)$.

另外要提前预处理对于 $i \in [1, n]$ 的 $\lfloor \log_2 i \rfloor$.

这时查询任意点 $x$ 的第 $k$ 级祖先, 首先 $O(1)$ 找到 $x$ 的第 $2^i$ 祖先 $Anc$ 满足 $2^i \leq k < 2^{i + 1}$.

这时, 可以保证 $Anc$ 所在的长链长度至少为 $2^i$. 而因为 $k < 2^{i + 1}$, 所以 $k - 2^i < 2^i$, 这时分类讨论:

• 目标在 $Anc$ 所在的长链上

  这时 $O(1)$ 查询 $Anc$ 链顶的 $InList$ 数组即可.

• 目标在 $Anc$ 所在的长链顶之上

  所以目标一定在 $Anc$ 链顶的 $List$ 中可以 $O(1)$ 查询.

实现

长链剖分和重链剖分类似, 分两次 DFS, 求出所需的几个值. 本题需要初始化几个数组, 然后 $O(1)$ 回答询问即可.

unsigned Seed, Log[500005], Bin[20], Hd(0), List[500005], InList[500005], m, n, Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
inline unsigned Rand(unsigned x) {
	x ^= x << 13, x ^= x >> 17, x ^= x << 5;return Seed = x;
}
unsigned long long Prt(0);
char Short(1);
struct Node {
  Node *Fa[20], *Son, *Bro, *LonSon, *Top;
  unsigned Len, DFSr, Deep;
}N[500005], *Root, *Top[500005];
void Link(Node *x, Node *y) {
  y->Bro = x->Son, x->Son = y;
}
void DFS1(Node *x) {
  Node *now(x->Son);
  x->Len = 1;
  while(now) {
    now->Deep = x->Deep + 1;
    now->Fa[0] = x;
    for (register unsigned i(0); now->Fa[i]; ++i) {
      now->Fa[i + 1] = now->Fa[i]->Fa[i];
    }
    DFS1(now);
    if(now->Len + 1 > x->Len) {
      x->Len = now->Len + 1;
      x->LonSon = now;
    }
    now = now->Bro;
  }
}
void DFS2(Node *x) {
  if(Short) Top[++Hd] = x, x->Top = x;
  Node *now(x->Son);
  x->DFSr = ++Cnt;
  InList[Cnt] = x - N;
  if(x->LonSon) {
    Short = 0;
    x->LonSon->Top = x->Top;
    DFS2(x->LonSon);
    Short = 1;
  }
  while(now) {
    if(now != x->LonSon) {
      DFS2(now);
    }
    now = now->Bro;
  }
}
signed main() {
  n = RD(), m = RD(), Seed = RD();
  for (register unsigned i(1); i <= n; ++i) {
    A = RD();
    if(!A) {
      Root = N + i;
      continue;
    }
    Link(N + A, N + i);
  }
  Root->Deep = 1;
  DFS1(Root), DFS2(Root);
  for (register unsigned i(1), L, R; i <= Hd; ++i) {
    register Node *x(Top[i]);
    L = x->DFSr, R = L + x->Len - 1;
    for (register unsigned j(L); j <= R; ++j) {
      List[j] = x - N;
      if(x->Fa[0]) x = x->Fa[0];
      else break;
    }
  }
  for (register unsigned i(1), j(0); i <= n; i <<= 1, ++j) {
    Log[i] = j, Bin[j] = i;
  }
  for (register unsigned i(3); i <= n; ++i) {
    Log[i] = max(Log[i], Log[i - 1]);
  }
  for (register unsigned i(1), Delta; i <= m; ++i) {
    A = ((Rand(Seed) ^ Ans) % n) + 1;
    B = (Rand(Seed) ^ Ans) % N[A].Deep;
    if(!B) {Ans = A, Prt ^= (unsigned long long)i * Ans; continue;}
    register Node *x(N[A].Fa[Log[B]]);
    B -= Bin[Log[B]];
    Delta = x->Top->Len - x->Len;
    if(Delta >= B) {
      Ans = InList[x->Top->DFSr + Delta - B];
    } else {
      Ans = List[x->Top->DFSr + B - Delta];
    }
    Prt ^= (unsigned long long)i * Ans;
  }
  printf("%llu\n", Prt);
  return Wild_Donkey;
}