混沌图像---双摆的游荡

　　前几天一个同事看到我写的双摆程序后问我:"这吊儿郎当的是什么玩意?",我当时给了他一个白眼说:"没文化,No education.这么高逼格的东西,你竟然说吊儿浪荡!"

上一篇文章是关于“三体”的混沌图像，这一篇就讲与之有些相似的“双摆”。双摆是物理学中的一个概念，依稀记得中学物理讲过单摆。先给下单摆与双摆的定义:

单摆：由一根不可伸长、质量不计的绳子，上端固定，下端系一个质点的装置。

双摆：是一个摆的支点装在另一摆的下部所形成的组合物体。双摆有两个摆角，所以有两个自由度。双摆是多自由度振动系统的最简单的力学模型之一，它也是一种混沌实例。

　　那么问题来了：双摆这种混沌系统，如果给定初始条件，以后任意时刻的运动状态都可以算出来吗？

　　答案是：理论上可以，但实际计算中，由于误差，会使运算结果与实际相差越来越大。这一点与三体很像，非线性数学就是这么任性。

下面四个GIF动画图像为双摆的录屏:

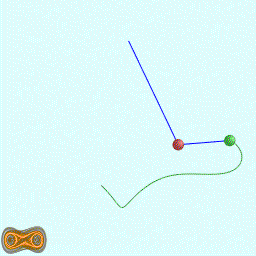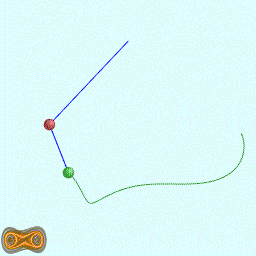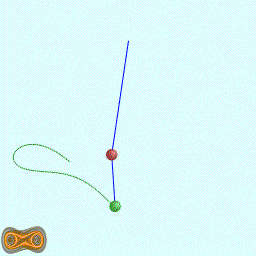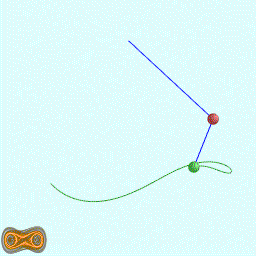
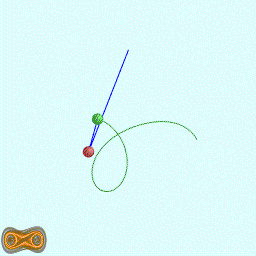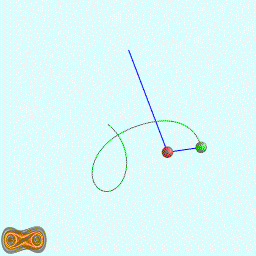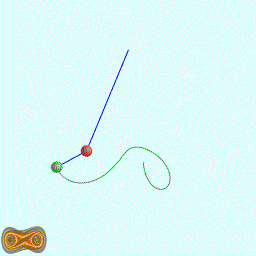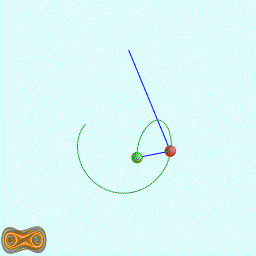
这里使用我定义语法的脚本代码生成混沌图像。相关软件参见:YChaos生成混沌图像。如果你对数学生成图形图像感兴趣,欢迎加入QQ交流群: 367752815.图像的生成方法是:使用第二个摆点的运动轨迹生成图像.

先上脚本代码：

[ScriptLines]
s=[static]p
w=[static]q
a=l*l*(m+n)
b=l*n*h*cos(s-w)
c=l*(n*h*sin(s-w)*v*v + (m+n)*g*sin(s))
d=n*h*l*cos(s-w)
e=n*h*h
f=n*h*(-l*sin(s-w)*u*u + g*sin(w))
i=(c*e - b*f)/(b*d - a*e)
j=(a*f - c*d)/(b*d - a*e)
u=u+i*t
v=v+j*t
s=s+u*t
w=w+v*t
x=l*sin(s) + h*sin(w)
y=-l*cos(s) - h*cos(w)

[Variables]
g=9.800000
h=2.000000
l=1.000000
m=1.000000
n=2.000000
p=1.000000
q=2.000000
t=0.000500
u=0.000000
v=0.000000

这里使用的是角度变化实现双摆，参考的资料是：

http://sebug.net/paper/books/scipydoc/double_pendulum.html

看图像：