样条之抛物线(一元三点)插值函数

      它是根据给定结点上的数值，用抛物插值计算指定插值点处的函数。一元三点插值算法是一种精度更高的插值算法，使用这种方法插值出来的曲线不像线性插值算法那样在分段点的地方出现折点，显得更为平滑。但它是使用二次函数来进行曲线的拟合，曲线中还是会有不平滑的情况。

关于插值与样条的介绍请看：http://www.cnblogs.com/WhyEngine/p/4020294.html

核心代码：

//////////////////////////////////////////////////////////////////////
// 一元三点等距插值
//////////////////////////////////////////////////////////////////////
static float GetValueParabolic(const void* valuesPtr, int stride, int n, float t)
{ 
    int i,j,k,m;
    float z,s,xi,xj;

    // 初值
    z=0.0;

    // 特例处理
    if (n < 1) 
    {
        return(z);
    }
    if (n == 1) 
    { 
        z = YfGetFloatValue(valuesPtr, stride, 0);  
        return(z);
    }
    if (n == 2)
    { 
        float y0 = YfGetFloatValue(valuesPtr, stride, 0); 
        float y1 = YfGetFloatValue(valuesPtr, stride, 1); 
        z = y0 + (y1 - y0)*t;
        return(z);
    }

    float xStep = 1.0f/(n - 1);

    // 开始插值
    if (t <= xStep) 
    { 
        k = 0; 
        m = 2;
    }
    else if (t >= (n-3)*xStep) 
    { 
        k = n-3; 
        m = n-1;
    }
    else
    { 
        i = (int)(t/xStep)+1;

        if (fabs(t-i*xStep) >= fabs(t-(i-1)*xStep))
        { 
            k = i-2; 
            m = i;
        }
        else 
        {
            k = i-1; 
            m = i+1;
        }
    }

    z = 0.0f;
    for (i = k; i <= m; i++)
    { 
        s = 1.0f; 
        xi = i*xStep;

        for (j = k; j <= m; j++)
        {
            if (j != i)
            { 
                xj = j*xStep; 
                // 抛物线插值公式
                s = s*(t-xj)/(xi-xj);
            }
        }

        z = z + s*YfGetFloatValue(valuesPtr, stride, i); 
    }

    return(z);
}

切图：

 

 

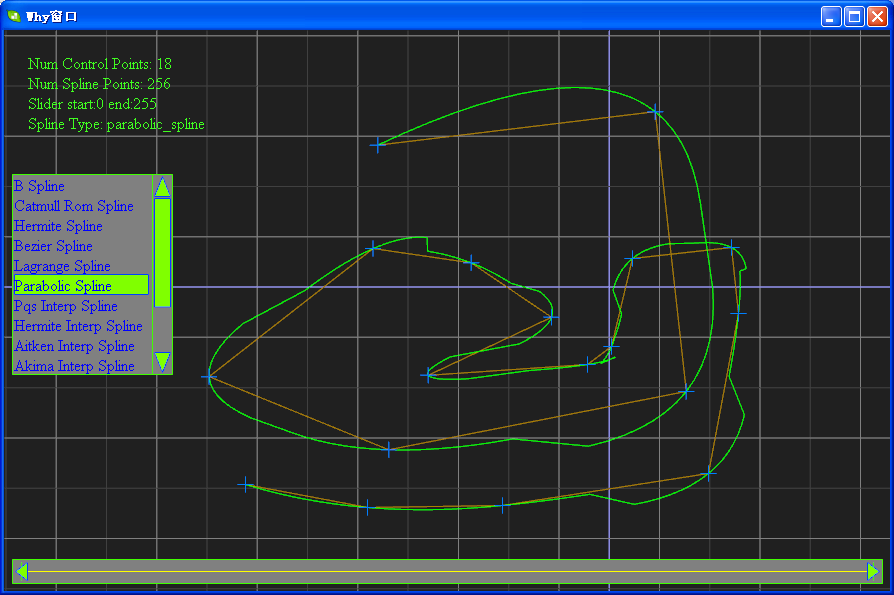
相关软件的下载地址为：https://files.cnblogs.com/WhyEngine/TestSpline.zip

……