B样条

在数学的子学科数值分析里，B-样条是样条曲线一种特殊的表示形式。它是B-样条基曲线的线性组合。B-样条是贝兹（贝塞尔）曲线的一种一般化，可以进一步推广为非均匀有理B样条(NURBS)，使得我们能给更多一般的几何体建造精确的模型。

常数B样条

常数B样条是最简单的样条。只定义在一个节点距离上，而且不是节点的函数。它只是不同节点段（knot span）的标志函数（indicator function）。

b_{j,0}(t) = 1_{[t_j,t_{j+1})} = \left\{\begin{matrix} 1 & \mathrm{} \quad t_j \le t < t_{j+1} \\ 0 & \mathrm{...} \end{matrix} \right.

线性B样条

线性B样条定义在两个相邻的节点段上，在节点连续但不可微。

b_{j,1}(t) = \left\{\begin{matrix} \frac{t - t_j}{t_{j+1} - t_j} & \mathrm{if} \quad t_j \le t < t_{j+1} \\ \frac{t_{j+2} - t}{t_{j+2} - t_{j+1}} & \mathrm{ } \quad t_{j+1} \le t < t_{j+2} \\ 0 & \mathrm{... } \end{matrix} \right.

三次B样条

一个片断上的B样条的表达式可以写作：

S_{i} (t) = \sum_{k=0}^3 \mathbf{P}_{i-3+k} b_{i-3+k,3} (t) \qquad \mbox{ , } t \in [0,1]

其中S_i是第i个B样条片断而P是一个控制点集，i和k是局部控制点索引。控制点的集合会是 $P_i^w = ( w_i x_i, w_i y_i, w_i z_i, w_i)$ 的集合，其中 $w_i$ 是比重，当它增加时曲线会被拉向控制点 $P_i$ ，在减小时则把曲线远离该点。

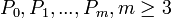片段的整个集合m-2条曲线（ $S_3,S_4,...,S_m$ ）由m+1个控制点（ $P_0,P_1,...,P_m, m \ge 3$ ）定义，作为t上的一个B样条可以定义为

S(t) = \sum_{i=0}^m \mathbf{P}_{i} b_{i,} (t)

其中i是控制点数，t是取节点值的全局参数。这个表达式把B样条表示为B样条基函数的线性组合，这也是这个名称的原因。

有两类B样条-均匀和非均匀。非均匀B样条相邻控制点间的距离不一定要相等。一个一般的形式是区间随着插入控制点逐步变小到0。

关于插值与样条的介绍请看：http://www.cnblogs.com/WhyEngine/p/4020294.html

核心代码：

 1 void    YcBSpline::BuildWeights()
 2 {
 3     ClearWeights();
 4 
 5     for (Yuint i = 0; i < 4; i++)
 6     {
 7         m_splineWeights[i] = (Yreal*)malloc((m_subD)*sizeof(Yreal));
 8         m_tangentWeights[i] = (Yreal*)malloc((m_subD)*sizeof(Yreal));
 9     }
10 
11     Yreal u, u_2, u_3;
12     for (Yuint i = 0; i < m_subD; i++)
13     {
14         u = (float)i / m_subD;
15         u_2 = u * u;
16         u_3 = u_2 * u;
17 
18         // 参见"游戏编程精粹1"P331
19         m_splineWeights[0][i] = (-1.0f*u_3 + 3.0f*u_2 - 3.0f*u + 1.0f)/6.0f;
20         m_splineWeights[1][i] = ( 3.0f*u_3 - 6.0f*u_2 + 0.0f*u + 4.0f)/6.0f;
21         m_splineWeights[2][i] = (-3.0f*u_3 + 3.0f*u_2 + 3.0f*u + 1.0f)/6.0f;
22         m_splineWeights[3][i] = ( 1.0f*u_3 + 0.0f*u_2 + 0.0f*u + 0.0f)/6.0f;
23 
24         // 参见"游戏编程精粹1"P333
25         m_tangentWeights[0][i] = (-1.0f*u_2 + 2.0f*u - 1.0f)*0.5f;
26         m_tangentWeights[1][i] = ( 3.0f*u_2 - 4.0f*u + 0.0f)*0.5f;
27         m_tangentWeights[2][i] = (-3.0f*u_2 + 2.0f*u + 1.0f)*0.5f;
28         m_tangentWeights[3][i] = ( 1.0f*u_2 + 0.0f*u + 0.0f)*0.5f;
29     }
30 }

切图：

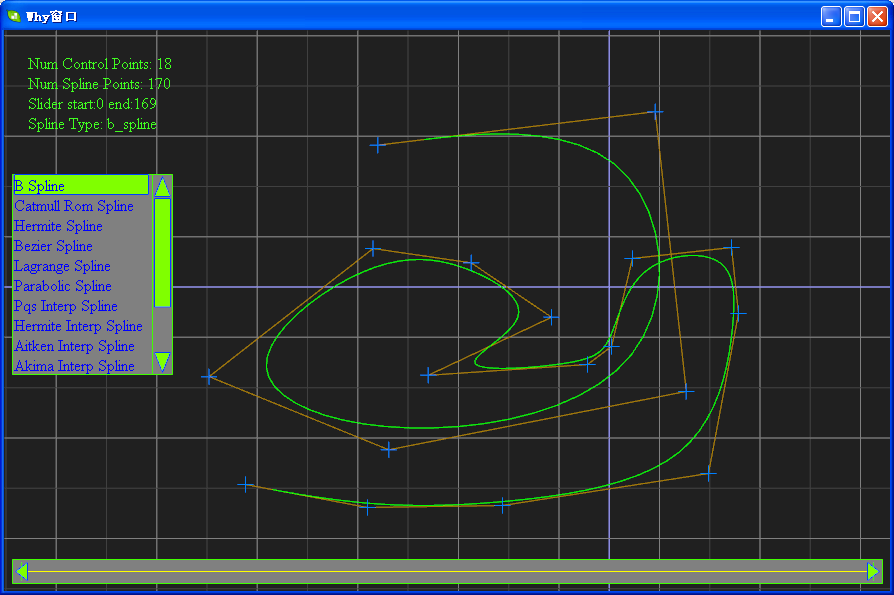
相关软件的下载地址为：https://files.cnblogs.com/WhyEngine/TestSpline.zip

最后要注意的是：B样条曲线不会经过其控制点。靠，我一直以为是经过的。因为B样条是我唯一在项目中使用过的。我用它来平滑游戏中角色刀光所划出的曲面，不过这种细节也没必要再去修改了。

posted on 2014-10-14 07:24 叶飞影阅读(8838) 评论(1) 编辑收藏举报