混沌数学之Duffing(杜芬)振子

杜芬振子 Duffing oscillator是一个描写强迫振动的振动子，由非线性微分方程表示

杜芬方程列式如下：

其中

• γ控制阻尼度
• α控制韧度
• β控制动力的非线性度
• δ驱动力的振幅
• ω驱动力的圆频率

杜芬方程没有解析解，但可用龙格－库塔法求得数值解。

当γ>0，杜芬振子呈现极限环振动；

相关软件:混沌数学及其软件模拟
相关代码:

//http://wenku.baidu.com/view/d51372a60029bd64783e2cc0.html?re=view
class DuffingEquation : public DifferentialEquation
{
public:
    DuffingEquation()
    {
        m_StartX = 1.0f;
        m_StartY = 1.0f;
        m_StartZ = 0.0f;

        m_ParamA = 2.09f;
        m_ParamB = 0.1f;
        m_ParamC = 0.5f;

        m_StepT = 0.002f;
    }

    void Derivative(float x, float y, float z, float& dX, float& dY, float& dZ)
    {
        dX = y;
        dY = m_ParamA*cosf(m_ParamC*m_ParamT) - m_ParamB*y + x - x*x*x;
        dZ = 0.0f;
    }

    bool IsValidParamA() const {return true;}
    bool IsValidParamB() const {return true;}
    bool IsValidParamC() const {return true;}
    bool IsValidParamT() const {return true;}
};

 

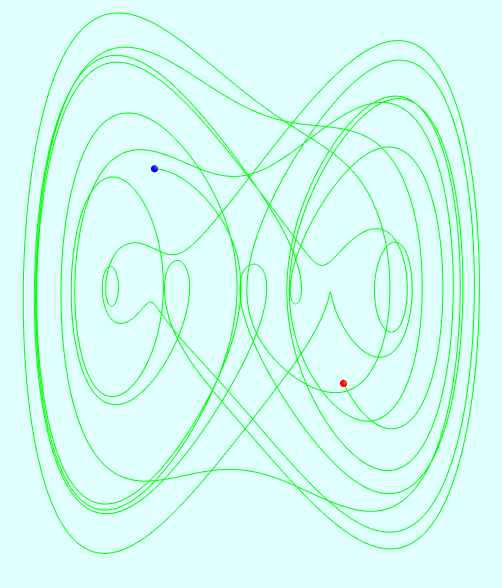
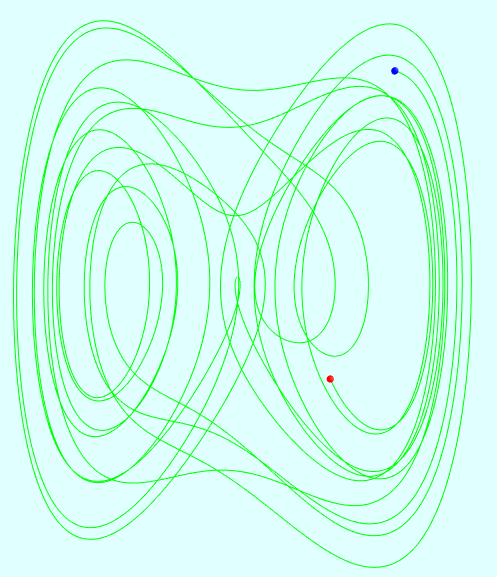
相关截图: