混沌数学之二维logistic模型

      上一节讲了logistic混沌模型,这一节对其扩充一下讲二维 Logistic映射.它起着从一维到高维的衔接作用，对二维映射中混沌现象的研究有助于认识和预测更复杂的高维动力系统的性态。通过构造一次藕合和二次祸合的二维Logistic映射研究了二维Logistic映射通向混沌的道路，分析了其分形结构和吸引盆的性质，指出选择不同的控制参数，二维映射可分别按Feigenbaum途径等走向混沌，并且指出在控制参数空间中的较大的区域。

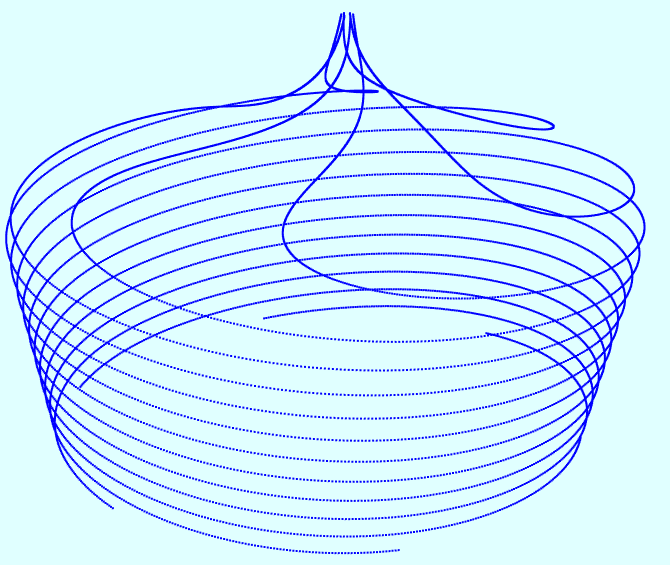
      二维滞后Logistic映射的数学方程为: x(n+1)=y(n);y(N+1)=u*y(n)*(1-x(n)), u属于(0,2.28),[x,y]属于(0,1)

      相关DEMO参见:混沌数学之离散点集图形DEMO

其代码与上一节的代码很相似:

// http://www.baike.com/wiki/logistic%E6%A8%A1%E5%9E%8B
class Logistic2DEquation : public DiscreteEquation
{
public:
    Logistic2DEquation()
    {
        m_StartX = 0.5f;
        m_StartY = m_StartX;

        m_ParamA = 2.003f;
    }

    void IterateValue(float x, float y, float& outX, float& outY) const
    {
        outX = y;
        outY = m_ParamA*y*(1-x);
    }

    bool IsValidParamA() const {return true;}
};

其图形与上一节的大不一样: