数学图形之克莱因瓶(klein bottle)
克莱因瓶是一种内外两面在同一个曲面上的图形.
在数学领域中,克莱因瓶(德语:Kleinsche Flasche)是指一种无定向性的平面,比如二维平面,就没有“内部”和“外部”之分。克莱因瓶最初的概念提出是由德国数学家菲利克斯·克莱因提出的。克莱因瓶和我上一篇讲的莫比乌斯带非常相像。一个是内外两面是在同一个曲面上,另一个是里外两面在同一个曲面上.
克莱因瓶的形状是,一个瓶子底部有一个洞,现在延长瓶子的颈部,并且扭曲地进入瓶子内部,然后和底部的洞相连接。
下面将展示几种莫比乌斯带的生成算法和切图,使用自己定义语法的脚本代码生成数学图形.相关软件参见:数学图形可视化工具,该软件免费开源.
以下是从维基上查到的公式
克莱因瓶的参数十分复杂:
写成我的脚本代码为:
vertices = D1:80 D2:160 u = from 0 to PI D1 v = from 0 to (2*PI) D2 a = sin(u) b = cos(u) c = sin(v) d = cos(v) e = 3*d - 3*b*b*d - 48*pow(b, 4)*d + 48*pow(b, 6)*d - 60*a + 5*b*d*a - 5*pow(b, 3)*d*a - 80*pow(b, 5)*d*a + 80*pow(b, 7)*d*a x = -2/15*b*(3*d - 30*a + 90*pow(b, 4)*a - 60*pow(b, 6)*a + 5*b*d*a) y = -1/10*a*e z = 2/15*(3 + 5*b*a)*c u = u*5 v = v*2.5
公式好复杂,我竟然写对了:

还有一个较简单的
写成我的脚本代码为:
vertices = D1:160 D2:160 u = from 0 to (4*PI) D1 v = from 0 to (2*PI) D2 a = sin(u) b = cos(u) c = sin(v) d = cos(v) e = sin(u/2) f = cos(u/2) x = b*(f*(sqrt(2) + d) + e*c*d) z = a*(f*(sqrt(2) + d) + e*c*d) y = -e*(sqrt(2) + d) + f*c*d
可惜这似乎是错的.生成的图形不是克莱因瓶.

此外,我还从别的地方找到关于克莱因瓶的公式.这两个公式生成的图形差不多,也不像克莱因瓶,而是一个8字形的曲线绕圈而成的曲面.
klein_bottle
#http://xahlee.info/surface/klein_bottle/klein_bottle.html vertices = D1:100 D2:100 u = from 0 to (PI*2) D1 v = from 0 to (PI*2) D2 a = 3 x = (a+cos[v/2]*sin[u]-sin[v/2]*sin[2*u])*cos[v] z = (a+cos[v/2]*sin[u]-sin[v/2]*sin[2*u])*sin[v] y = sin[v/2]*sin[u]+cos[v/2]*sin[2*u]

klein
#http://www.mathcurve.com/surfaces/klein/klein.shtml vertices = D1:100 D2:100 u = from 0 to (PI*2) D1 v = from 0 to (PI*2) D2 a = rand2(1, 10) b = rand2(1, 10) x = [a + b*(cos(u/2)*sin(v) - sin(u/2)*sin(2*v))]*cos(u) z = [a + b*(cos(u/2)*sin(v) - sin(u/2)*sin(2*v))]*sin(u) y = b*[sin(u/2)*sin(v) + cos(u/2)*sin(2*v)]




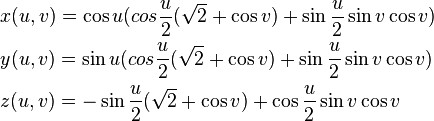

 浙公网安备 33010602011771号
浙公网安备 33010602011771号