Codeforces Round #323 (Div. 1) A. GCD Table

A. GCD Table

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The GCD table G of size n × n for an array of positive integers a of length n is defined by formula

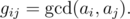
Let us remind you that the greatest common divisor (GCD) of two positive integers x and y is the greatest integer that is divisor of both xand y, it is denoted as 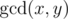. For example, for array a = {4, 3, 6, 2} of length 4 the GCD table will look as follows:

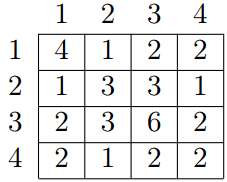
Given all the numbers of the GCD table G, restore array a.

Input

The first line contains number n (1 ≤ n ≤ 500) — the length of array a. The second line contains n2 space-separated numbers — the elements of the GCD table of G for array a.

All the numbers in the table are positive integers, not exceeding 109. Note that the elements are given in an arbitrary order. It is guaranteed that the set of the input data corresponds to some array a.

Output

In the single line print n positive integers — the elements of array a. If there are multiple possible solutions, you are allowed to print any of them.

Sample test(s)

input

4
2 1 2 3 4 3 2 6 1 1 2 2 1 2 3 2

output

4 3 6 2

input

1
42

output

42 

input

2
1 1 1 1

output

1 1 

 题目大意：给出你一个n，然后后边n*n个数，是n个数序列的gcd表的值(无序），输出这n个数

对角线上的元素就是ans[i]，而且在所在行和列中最大，

首先可以确定的是最大的元素一定是ans[i]之一，这让人想到到了排序。

经过排序后，每次选最大的数字，如果不是之前更大数字的gcd，那么只能是ans[i]之一。

ac代码

93 ms

5576 KB

 

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<map>
#include<iostream>
using namespace std;
#define LL __int64
int cmp(LL a,LL b)
{
	return a>b;
}
LL a[350500],ans[355000];
LL gcd(LL a,LL b)
{
	int t;
	if(a<b)
	{
		t=b;
		b=a;
		a=t;
	}
	if(b==0)
		return a;
	return gcd(b,a%b);
}
int main()
{
	int n;
	while(scanf("%d",&n)!=EOF)
	{
		int sz=n*n;
		int i;
		map<LL,LL>mp;
		for(i=0;i<sz;i++)
			scanf("%I64dd",&a[i]);
		sort(a,a+sz,cmp);
		int c=0,j=0;
		ans[c++]=a[j++];
		for(i=1;i<n;i++)
		{
			while(j<sz&&mp[a[j]])
			{
				mp[a[j]]--;
				j++;
			}
			if(j==sz)
				break;
			for(int k=c-1;k>=0;k--)
				mp[gcd(ans[k],a[j])]+=2;
			ans[c++]=a[j++];
		}
		for(i=c-1;i>=0;i--)
		{
			if(i==c-1)
				printf("%I64d",ans[i]);
			else
				printf(" %I64d",ans[i]);
		}
	}
}