高手训练 线段树T3 P1753：区间连通性

线段树/标记永久化

复杂度 \(O(nlogn)\)

题解有误，并非所有与线段树节点[l,r]相交的所有区间[s.t]都要存入vector

插入区间[s,t]时，我们覆盖了一段完整的区间，如图

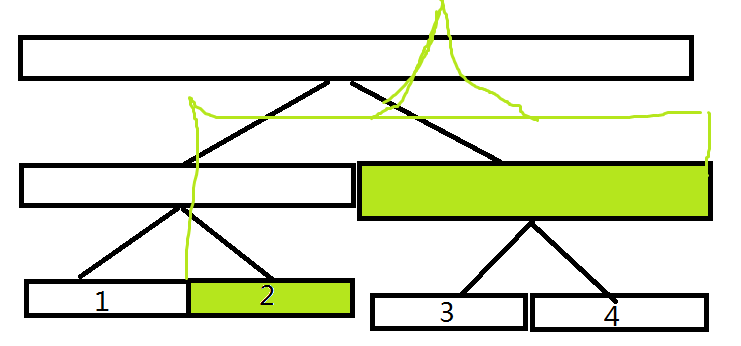
实质上是覆盖了表面的一层，即标记不下传

故我们merge时要考虑每一层的vector

插入时，如果两个区间恰好相接，也视作互相到达，所以合并时用(s,t)合并，插入时用[s+1,t-1]插入

由于区间按长度从小到大插入，故不存在这样的情况：

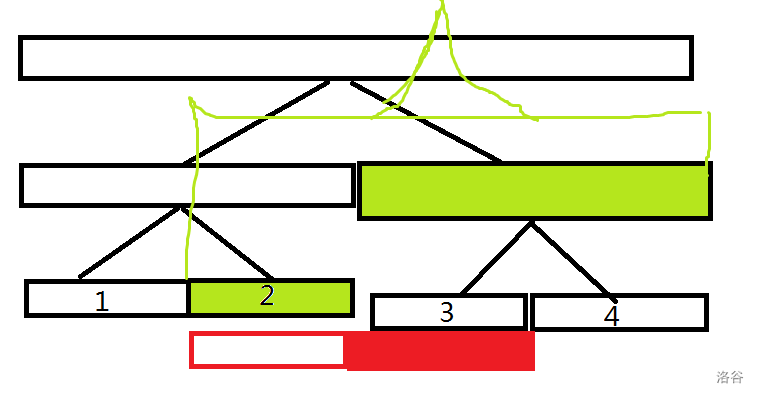
故merge的区间一定是两两可达的，用并查集来维护这种关系

最后，若区间存在包含关系，则A可以到达B，B不能到达A（一端端点重合也算），则特判即可，由于端点可能重合，故不能只判断一个端点

代码非常简单：

#include<bits/stdc++.h>
using namespace std;

#define go(i,a,b) for(int i=a;i<=b;++i)
#define com(i,a,b) for(int i=a;i>=b;--i)
#define mem(a,b) memset(a,b,sizeof(a))
#define ls rt<<1
#define rs rt<<1|1

const int inf=0x3f3f3f3f,N=2e5+10;

int n,m,op[N],a[N],b[N],c[N],d[N],f[N],rk[N],id,tot;
vector<int>inter[N<<2];

void read(int &x){
	x=0;char c=getchar(),f=1;
	while(!isdigit(c)){ if(c=='-') f=-1; c=getchar(); }
	while(isdigit(c)){ x=x*10+c-'0'; c=getchar(); }
	x*=f;
}
inline int find(int x){ return f[x]=f[x]==x?x:find(f[x]); }

void merge(int rt,int l,int r,int k){
	for(int i=0;i<inter[rt].size();++i){
		int x=inter[rt][i];
		x=find(x);
		f[x]=id;
		c[id]=min(c[id],c[x]);
		d[id]=max(d[id],d[x]);
	}
	inter[rt].clear();
	if(l==r) return;
	int mid=l+r>>1;
	if(k<=mid) merge(ls,l,mid,k);
	else merge(rs,mid+1,r,k);
}

void insert(int rt,int l,int r,int x,int y,int k){
	if(l>=x&&r<=y){
		inter[rt].push_back(k);
		return; 
	}
	int mid=l+r>>1;
	if(x<=mid) insert(ls,l,mid,x,y,k);
	if(y>mid) insert(rs,mid+1,r,x,y,k);
}

int main(){
	//freopen("input.txt","r",stdin);
	read(n);
	go(i,1,n){
		read(op[i]),read(a[i]),read(b[i]);
		if(op[i]==1) rk[++tot]=a[i],rk[++tot]=b[i];
	}
	sort(rk+1,rk+tot+1);
	tot=unique(rk+1,rk+tot+1)-rk-1;
	go(i,1,n) if(op[i]==1){
		a[i]=lower_bound(rk+1,rk+tot+1,a[i])-rk;
		b[i]=lower_bound(rk+1,rk+tot+1,b[i])-rk;
	}
	int x,y;
	go(i,1,n){
		if(op[i]==1){
			f[++id]=id,c[id]=a[i],d[id]=b[i];
			merge(1,1,tot,a[i]);
			merge(1,1,tot,b[i]);
			insert(1,1,tot,c[id]+1,d[id]-1,f[id]);
		}
		else{
			x=find(a[i]),y=find(b[i]);
			if(x==y) puts("YES");
			else{
				if(c[x]>c[y]&&c[x]<d[y]||d[x]>c[y]&&d[x]<d[y]) puts("YES");
				else puts("NO");
			}
		}
	}
	return 0;
}