《考研机试》（四）机试题精讲

1.题（一）

 

解析：

　　只需要知道一个三位数k：个位 = k%10

　　　　　　　　　　　　　  十位 = k/10%10

　　　　　　　　　　　　　  百位 = k/100 

代码：

#include<iostream>
using namespace  std;

int main() {
	for(int i=100; i<1000; i++){
		int gewei = i%10;
		int shiwei = i/10%10;
		int baiwei = i/100;
		int sum = (gewei*gewei*gewei)+(shiwei*shiwei*shiwei)+(baiwei*baiwei*baiwei);
		if( i==sum ){
			cout << i << " ";
		}
	} 
	return 0;
}

2.题（二）

 

 解析：两种思路：1.i，j两个指针，插入排序，i是j的前面，如果i，j一样，那么j++跳过重复元素

　　　　　　　　 2.i，j两个指针使用辅助数组，辅助数组b大小=原数组a，刚开始赋值b[0]=a[0]，从0开始比较，如果相等原数组指针i++，否则存到辅助数组里去

代码：

#include<iostream>
using namespace  std;

void deleteSame1(int a[], int n){
	int i, j;//定义2个指针 
	for(i=0, j=1; j<n; j++){//i指向前一位,j指向后一位 
	
		if( a[i]!=a[j] ){//前后不相等 
			a[++i] = a[j];//相当于a[++0]=a[1]即a[1]=a[1],不变 
		}
		//否则前后相等,j++,i不变，即相当于跳过 
	}
	//打印 
	for(int k=0; k<=i; k++){
		cout << a[k] << " ";
	}
}

void deleteSame2(int a[], int n){
	int *b = new int[n];//辅助数组 
	int i=0, k=0;
	b[0] = a[0];//第一位等于原数组a第一位
	while(i<n){
		if( a[i]==b[k] ){//前后相等不存取 
			i++;
			continue;
		}else{//不相等存到辅助数组里 
			b[++k] = a[i++]; 
		}
	}
	//打印 
	for(int j=0; j<=k; j++){
		cout << b[j] << " ";
	} 
} 

int main() {
	int a[9] = {7,10,10,21,30,42,42,42,51};
	deleteSame1(a, 9);//方法1 
	deleteSame2(a, 9);//方法2 
	return 0;
}

3.题（三）

 

 

 

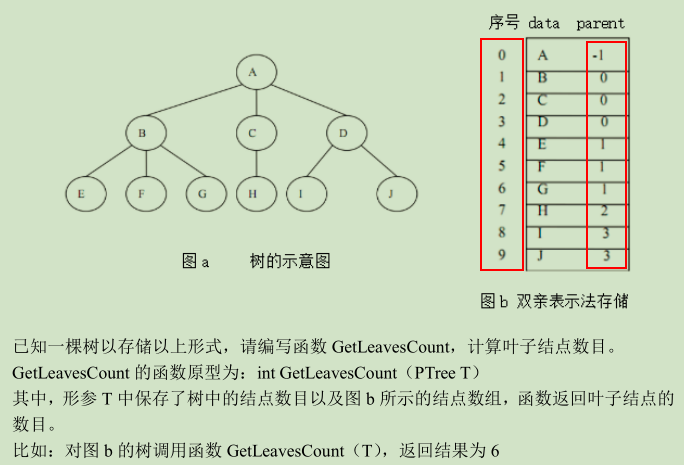
 解析：找到叶子节点 = 全部节点 — 非叶子节点

　　　 如果一个结点序号i，只要有结点的parent == i，那么结点i就是非叶子节点

代码：

#include<iostream>
using namespace std;
#define MAX_TREE_SIZE 100

//结点结构体： 
typedef struct {
	char data; //结点数据域
	int parent; //结点双亲在数组中的位置
} PTNode;

//树结构体： 
typedef struct {
	PTNode nodes[MAX_TREE_SIZE];  //存储树中所有的结点
	int n; //树中的结点数，n 不超过 100
}PTree;

/*
算法思想：
		  遍历结点数组，当该结点的序号有另外一个节点指向时，那么该结点为非叶节点，
		  当遍历完结点时，没有一个结点的指针指向该序号的话，那么该结点即是叶结点。
*/

//返回树中叶子结点个数=节点数目-非叶子节点数目 
int GetLeavesCount(PTree T) {
	int count = 0;//统计非叶结点的个数，转换一下思考方式，否则很难直接统计叶结点个数
	//非叶子节点：只要是有其他结点指向该结点就是非叶子结点 
	for(int i=0; i<T.n; i++){ 
		for (int j=0; j<T.n; j++) {
			if (i == j){//自己指向自己不算
			   continue;
			}else if (T.nodes[j].parent == i) {
				count++;
				break;//break是因为一个结点有许多孩子,count只要加一次 
                     //count统计的是非叶子结点 
			}
		}
	} 
	return T.n-count;
}

int main() {
	cout << "请输入树的结点的个数";
	int n = 0;
	cin >> n;
	PTree pt;
	pt.n = n;
	cout << "请输入每个结点的信息：" << endl;
	for (int i = 0; i < n; i++) {//输入结点的数据域和结点双亲在数组中的位置
		cin >> pt.nodes[i].data;//数据 
		cin >> pt.nodes[i].parent;//父节点位置 
	}
	int leaves=GetLeavesCount(pt);
	cout << "叶子节点数目=" << leaves << endl;
	return 0;
}